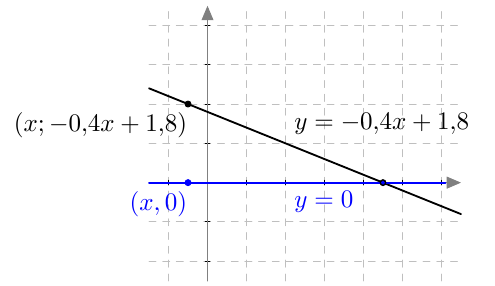Kurssissa MAB2 opittiin, että ensimmäisen asteen polynomifunktion kuvaaja on aina suora. Jos funktio on muotoa $$f(x) = ax + b,$$ missä $a \neq 0$, niin sen kuvaaja on suora, jonka yhtälö on $$y = ax + b.$$ Suoran yhtälö ilmaisee, miten suoran pisteiden $y$-koordinaatit riippuvat $x$-koordinaateista. Sen avulla voidaan löytää pisteitä, joiden kautta suora kulkee. Seuraava tehtävä valaisee asiaa tarkemmin.
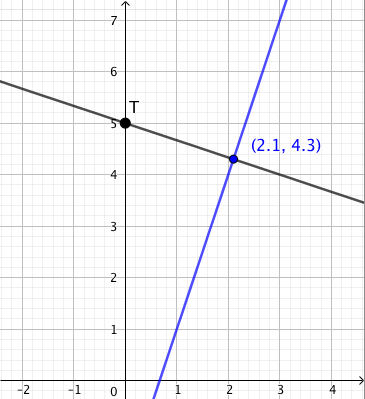
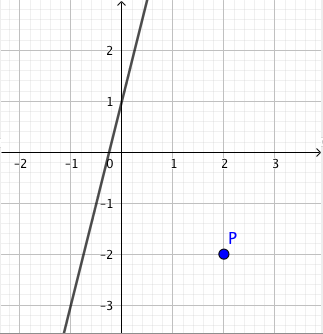
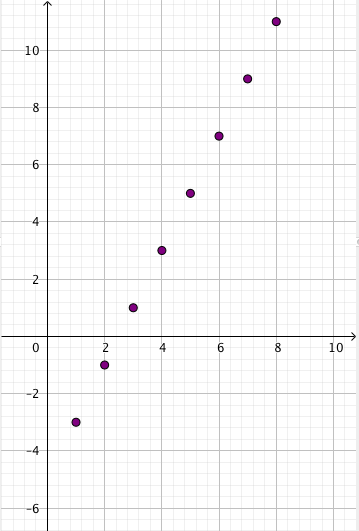
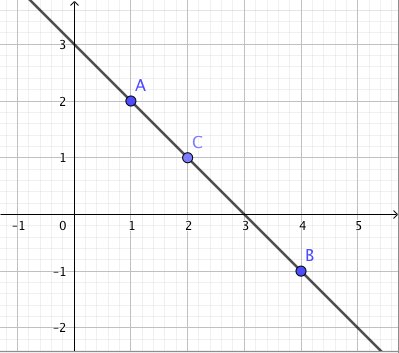
Suoran yhtälö on $y = -x + 3$.
- Suoran pisteen $x$-koordinaatti on $x = 1$. Laske suoran yhtälön avulla tämän pisteen $y$-koordinaatti. Merkitse piste koordinaatistoon.
- Suoran pisteen $x$-koordinaatti on $x = 4$. Laske tämän pisteen $y$-koordinaatti ja merkitse piste koordinaatistoon. Piirrä näiden kahden pisteen kautta kulkeva suora.
- Valitse $x$-koordinaatille jokin kolmas arvo (esimerkiksi lukujen $-1$ ja $7$ väliltä) ja laske sitä vastaavan suoran pisteen $y$-koordinaatti. Osuuko tämä piste b-kohdassa piirtämällesi suoralle?
- $y = -1 + 3 = 2$, joten piste on $(1,2)$.
- $y = -4 + 3 = -1$, joten piste on $(4,-1)$.
- Esimerkiksi jos $x = 2$, niin $y = -2 + 3 = 1$. Piste $(2,1)$ on suoran $y = -x+3$ piste.
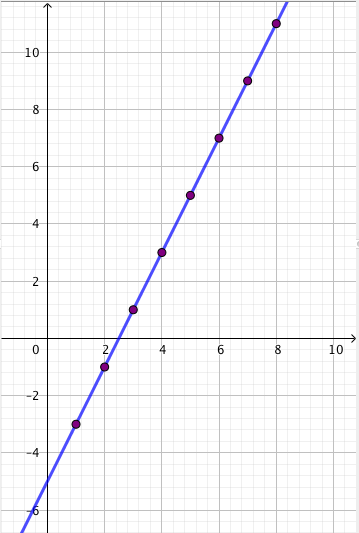
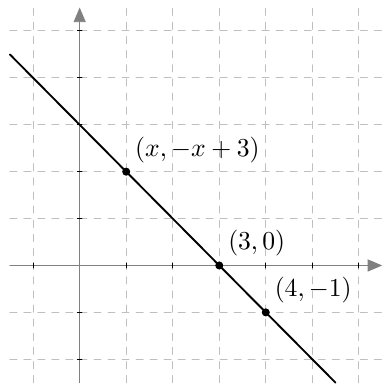
Suoran yhtälö siis kertoo, miten suoran pisteen $y$-koordinaatti riippuu pisteen $x$-koordinaatista. Esimerkiksi suoran $y = -x + 3$ kaikki pisteet ovat muotoa $(x, -x+3)$.
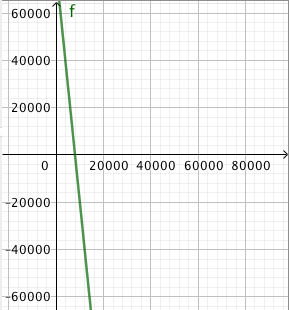
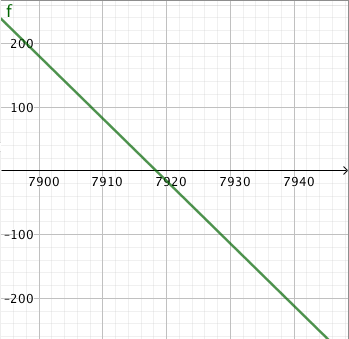
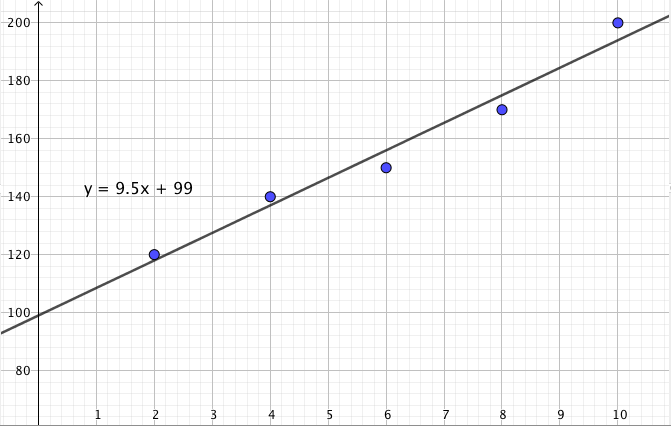
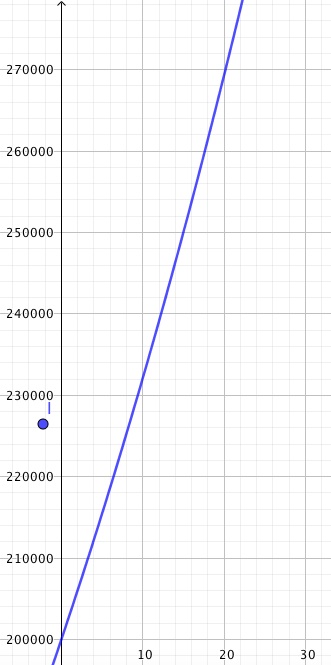
Tehtävänä on selvittää, ovatko pisteet $A = (2116, 894)$ ja $B = (15668, 4273)$ suoralla, jonka yhtälö on $y = 0{,}25x + 365$.
- Selvitä suoran yhtälön avulla, mikä on suoran pisteen $y$-koordinaatti, jos $x$-koordinaatti on $x = 2116$. Onko piste $A$ suoralla?
- Selvitä suoran yhtälön avulla, mikä on suoran pisteen $y$-koordinaatti, jos $x$-koordinaatti on $x = 15668$. Onko piste $B$ suoralla?
- $y = 0{,}25 \cdot 2116 + 365 = 894$, joten piste $A = (2116, 894)$ on suoralla.
- $y = 0{,}25 \cdot 15668 + 365 = 4282$, joten piste $B = (15668, 4273)$ ei ole suoralla.
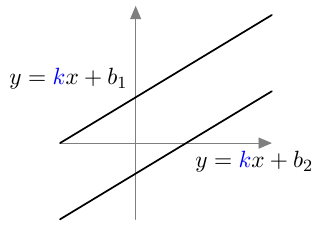
Suoran yhtälössä $$ y = kx + b $$ vakio $b$ ilmaisee, millä korkeudella suora leikkaa $y$-akselin. Kerroin $k$ puolestaan on kyseisen suoran kulmakerroin.
MÄÄRITELMÄ: KULMAKERROIN
Suoran yhtälössä $y = kx + b$ esiintyvä kerroin $k$ on suoran kulmakerroin.
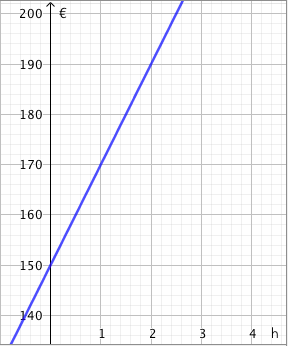
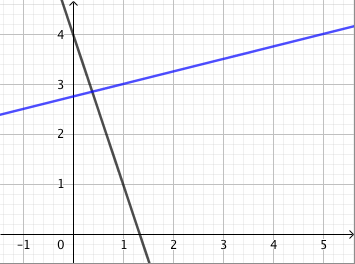
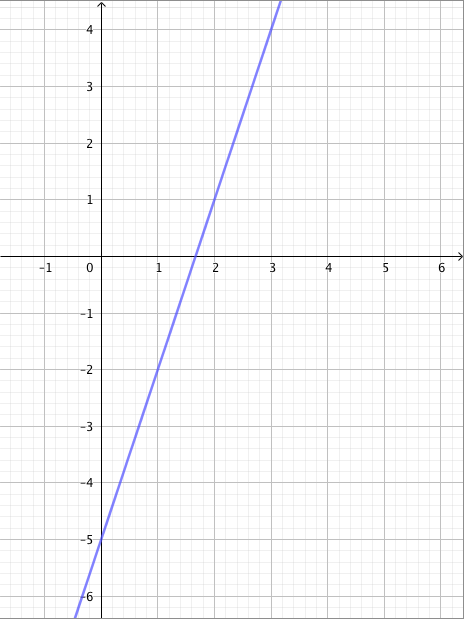
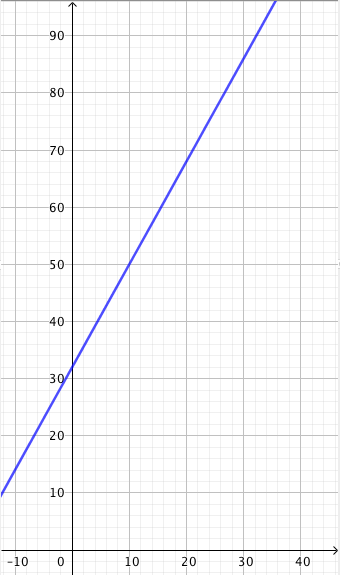
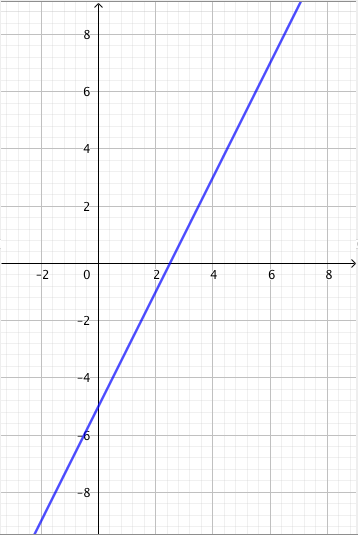
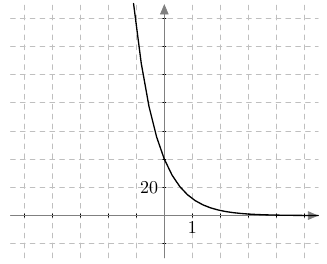
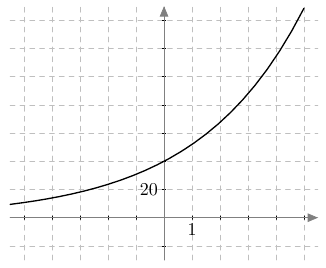
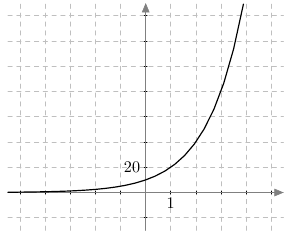
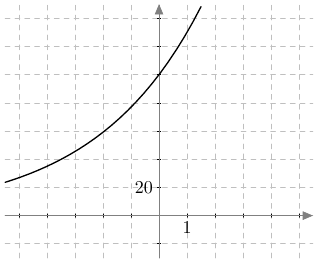
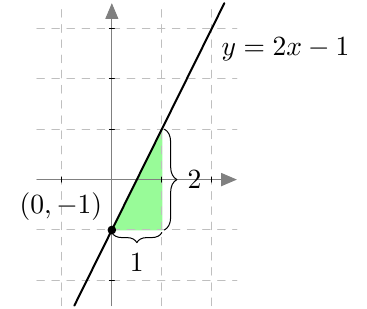
Alla on näkyvissä suora, jonka kulmakerroin on $k = 2$. Tämä näkyy kuvassa siten, että kun siirrytään yksi ruutu oikealle, suora nousee aina kaksi ruutua ylöspäin.
Seuraavassa tehtävässä harjoitellaan tunnistamaan, miten suoran kulmakerroin $k$ ja vakio $b$ vaikuttavat suoran suuntaan ja sijaintiin koordinaatistossa.
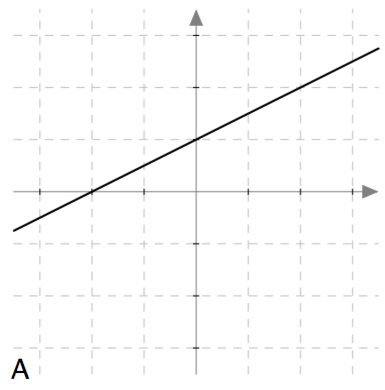
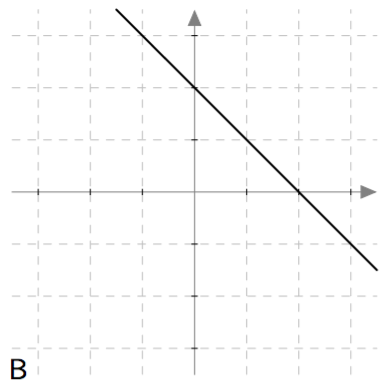
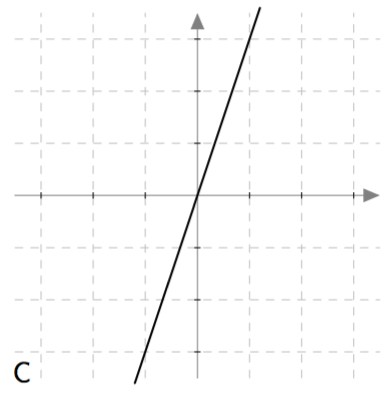
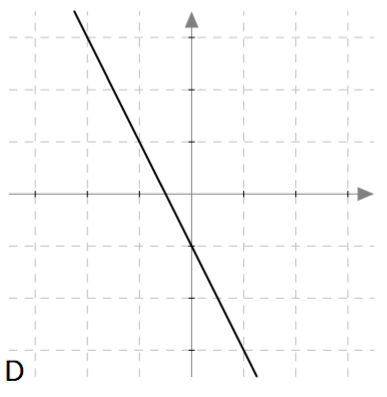
Yllä on näkyvissä erilaisia suoria. Kopioi alla oleva taulukko vihkoosi ja täydennä se. Päättele sen jälkeen vastaukset alla oleviin kysymyksiin.
| Suora | Kulmakerroin | Korkeus, jolla leikkaa $y$-akselin | Kuva |
| $\ y = 3x \phantom{ {} + 11} \ $ | | | |
| $\ y = -2x-1 \ $ | | | |
| $\ y = 0{,}5x+1 \ $ | | | |
| $\ y = -x+2\phantom{1} \ $ | | | |
Miten yhtälöstä $y = kx + b$ voi päätellä,
- onko kysymyksessä nouseva suora (kuten kuvissa A ja C) vai laskeva suora (kuten kuvissa B ja D)?
- millä korkeudella suora leikkaa $y$-akselin?
- kuinka monta ruutua suora nousee tai laskee, kun siirrytään yhden ruudun verran oikealle?
Kuten edellisessä tehtävässä havaittiin, suora $y = kx + b$ on
- nouseva, jos $k > 0$ eli kulmakerroin on positiivinen
- laskeva, jos $k < 0$ eli kulmakerroin on negatiivinen.
Lisäksi kulmakerroin vaikuttaa suoran jyrkkyyteen: mitä lähempänä nollaa kulmakerroin on, sitä loivemmin suora nousee tai laskee.
Tässä tehtävässä selvitetään missä pisteessä suora $y = kx + b$ leikkaa $y$-akselin.
- Jos piste on $y$-akselilla, mitä voit päätellä sen $x$-koordinaatin arvosta? Voit tutkia asiaa valitsemalla pisteitä $y$-akselilla ja päättelemällä niiden $x$-koordinaattien arvot.
- Jos pisteen $x$-koordinaatti on $x = 0$ ja piste on suoralla $y = 3x + 5$, mikä on sen $y$-koordinaatti?
- Jos pisteen $x$-koordinaatti on $x = 0$ ja piste on suoralla $y = kx + b$, mikä on sen $y$-koordinaatti?
- Päättele edellisten kohtien avulla, missä pisteessä suora $y = kx + b$ leikkaa $y$-akselin.
- $x = 0$
- $y = 3 \cdot 0 + 5 = 5$
- $y = k \cdot 0 + b = b$
- Suora $y = kx + b$ leikkaa $y$-akselin pisteessä $(0,b)$.
Edellisen tehtävän tulos voidaan muotoilla seuraavaksi teoreemaksi:
TEOREEMA
Suora $y = kx + b$ leikkaa $y$-akselin pisteessä $(0,b)$.
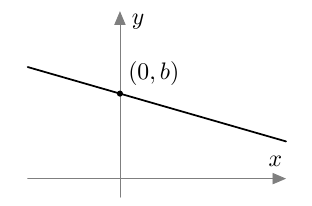
Jos suoran yhtälö tunnetaan, voi suoran piirtää koordinaatistoon monella menetelmällä.
- Piirrä suora $y = -2x+5$ kuvaaja seuraavasti: Määritä suoran yhtälön avulla jotkin kaksi pistettä, joiden kautta kuvaaja kulkee. Piirrä näiden kautta kulkeva suora.
- Piirrä suora $y = x+3$ kuvaaja seuraavasti: Päättele funktion lausekkeesta, millä korkeudella kuvaaja leikkaa $y$-akselin ja mikä on kuvaajan kulmakerroin. Piirrä suora näiden tietojen avulla.
- Tarkista piirrokset piirtämällä kumpikin kuvaaja laskimella tai tietokoneella.
- Kuvaaja kulkee esimerkiksi pisteiden $(0,5)$ ja $(1,3)$ kautta. (Voit keksiä $x$-koordinaatin itse ja laskea sitä vastaavan $y$-koordinaation suoran yhtälön avulla.)
- Kuvaaja leikkaa $y$-akselin korkeudella 3 eli pisteessä $(0,3)$. Kuvaajan kulmakerroin on $1$. Kuvaaja siis nousee aina yhden ruudun, kun siirrytään yhden ruudun verran oikealle.
Edellä havaittiin, että suoran kulmakerroin kuvaa suoran jyrkkyyttä. Jos tunnetaan suoran kahden pisteen koordinaatit, voidaan kulmakerroin määrittää laskemalla $y$-koordinaattien erotus, $x$-koordinaattien erotus ja näiden erotusten osamäärä:
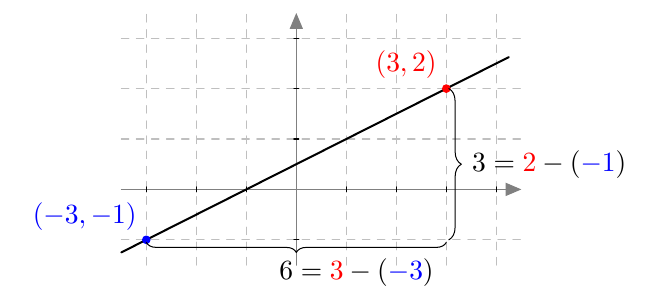
Yllä näkyvän suoran kulmakertoimeksi saadaan näin \begin{align} k &= \frac{\text{$y$:n muutos} }{\text{$x$:n muutos} } = \dfrac{\textcolor{red}{2}-(\textcolor{blue}{-1})}{\textcolor{red}{3} - (\textcolor{blue}{-3})} \\[2mm] &= \dfrac{3}{6} = \dfrac{1}{2} = 0{,}5. \end{align} Silmämääräisesti arvioituna tulos on järkevä, sillä kun siirrytään yksi ruutu oikealle, suora näyttää nousevan aina puoli ruutua ylöspäin.
Ilmaistaan suoran kulmakertoimen määrittäminen vielä yleisenä sääntönä:
TEOREEMA
Oletetaan, että $\textcolor{blue}{x_1} \neq \textcolor{red}{x_2}$. Pisteiden $\textcolor{blue}{(x_1,y_1)}$ ja $\textcolor{red}{(x_2,y_2)}$ kautta kulkevan suoran kulmakerroin on $$k = \frac{\text{$y$:n muutos} }{\text{$x$:n muutos} } = \frac{\textcolor{red}{y_2}-\textcolor{blue}{y_1}}{\textcolor{red}{x_2}-\textcolor{blue}{x_1}}$$ 
Määritä suorien kulmakertoimet alla olevan kuvan avulla.
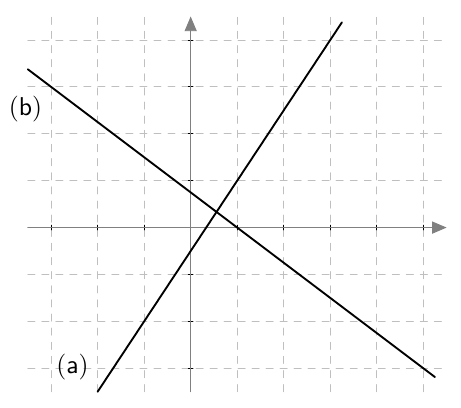
Vinkki: Valitse pisteet, joiden koordinaatit ovat kokonaislukuja. Silloin saat tarkan tuloksen.
- $k = \dfrac{3}{2} = 1{,}5$
- $k = -\dfrac{3}{4} = -0{,}75$
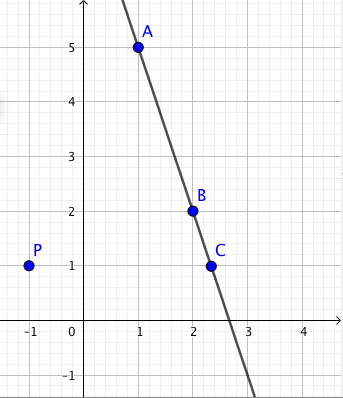
Määritä kulmakerroin pisteiden $A$ ja $B$ kautta kulkevalle suoralle ja päättele, onko suora nouseva vai laskeva.
- $A = (1,-2)\ $ ja $\ B = (3,4)$
- $A = (-2,6)\ $ ja $\ B = (3,2)$
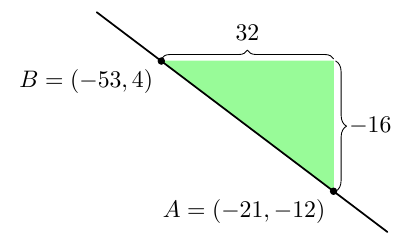
- $A = (-21,-12)\ $ ja $\ B = (-53,4)$
Vinkki: kuvan tai mallikuvan hahmotteleminen yleensä helpottaa oikeiden johtopäätösten tekemistä.
- Nouseva. Kulmakerroin $k = \dfrac{6}{2} = 3$.
- Laskeva. Kulmakerroin $k = -\dfrac{4}{5} = -0{,}8$.
- Laskeva. Kulmakerroin $k = -\dfrac{16}{32} = -0{,}5$.
Tässä voi hahmotella pisteiden $A$ ja $B$ keskinäisen sijainnin mallikuvan avulla: piste $B$ on enemmän vasemmalla ja ylempänä kuin piste $A$.
Suoran kulmakertoimesta voidaan päätellä muutoksen nopeus. Seuraavat tehtävät valaisevat asiaa.
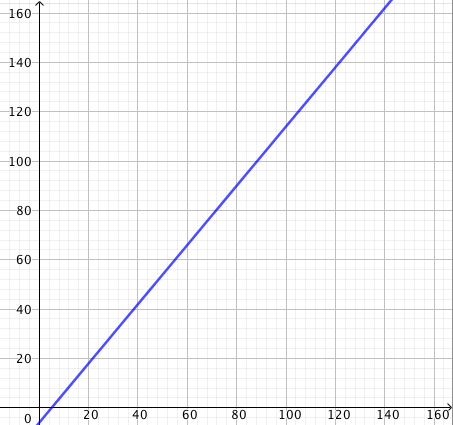
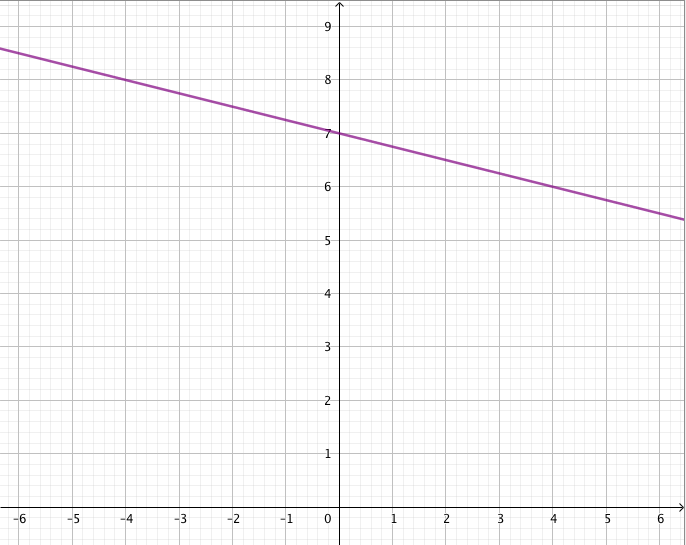
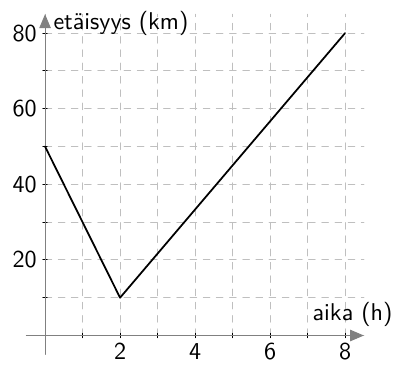
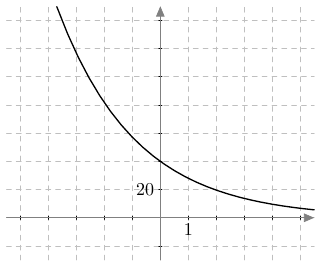
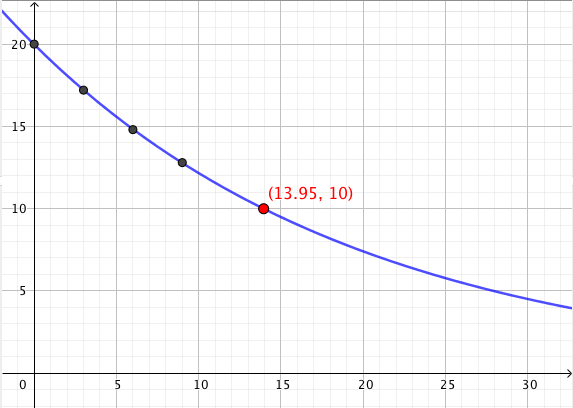
Erään sääaseman mittauspisteessä lämpötila laski kesäyönä tasaisesti niin, että yön viilein hetki oli klo 3 aamuyöllä. Kello 20.00 lämpötilaksi mitattiin 20,7 astetta. Alla oleva kuvaaja esittää lämpötilaa ajan funktiona (vaaka-akselilla aika tunteina klo 20.00 alkaen, pystyakselilla lämpötila celsiusasteina).
- Mikä oli kuvaajan mukaan lämpötila yöllä klo 0.00?
- Mikä on suoran kulmakerroin?
- Mikä on lämpötilan muutosnopeus (astetta/tunti)?
Anna vastaukset yhden desimaalin tarkkuudella.
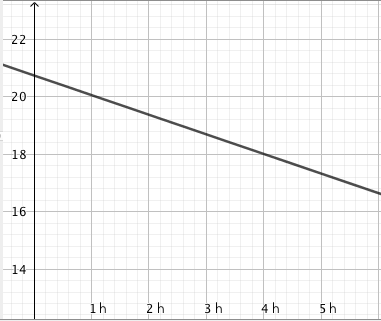
- Lämpötila oli noin 18,0 astetta.
Kun kello on 0.00, on kulunut 4 tuntia siitä, kun kello oli 20.00. Kuvaaja kulkee pisteen $(4; 18{,}0)$ kautta, joten klo 0.00 lämpötila on noin 18,0 astetta. - Kulmakerroin on $k \approx -0{,}7$. Sen voi laskea esimerkiksi käyttäen pisteitä $(0;20{,}7)$ ja $(4;18{,}0)$.
- Kuvaajasta nähdään, että lämpötila laskee neljässä tunnissa noin 2,7 astetta. Siis lämpötila laskee noin $2{,}7/4 \approx 0{,}7$ astetta/tunti. Lämpötilan muutosnopeus on sama kuin lämpötilaa esittävän suoran kulmakerroin.
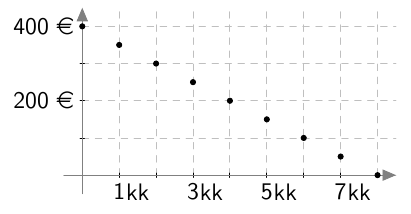
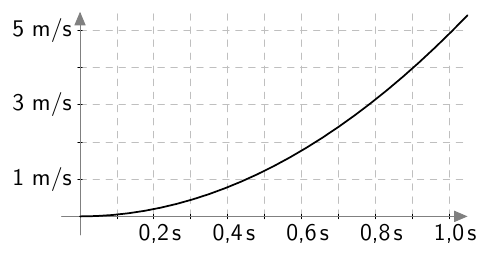
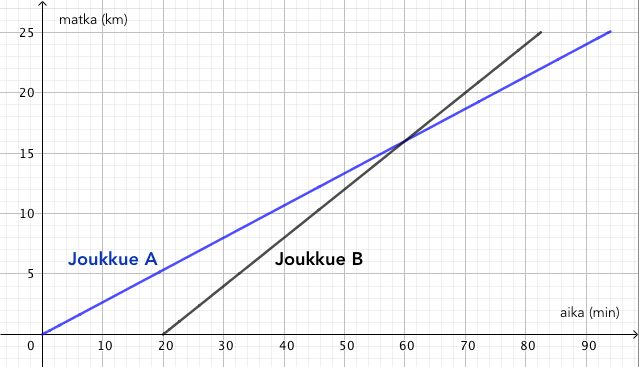
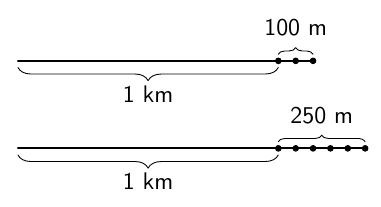
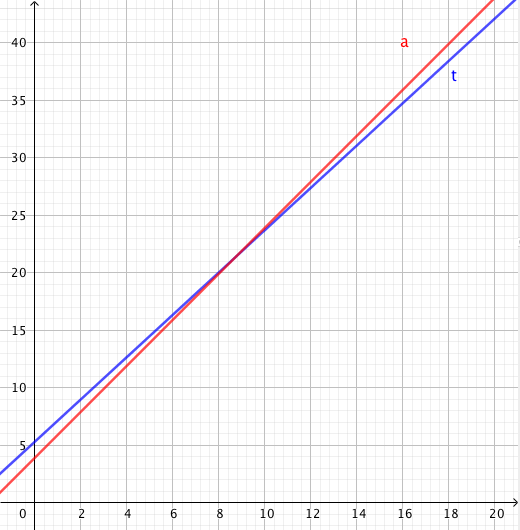
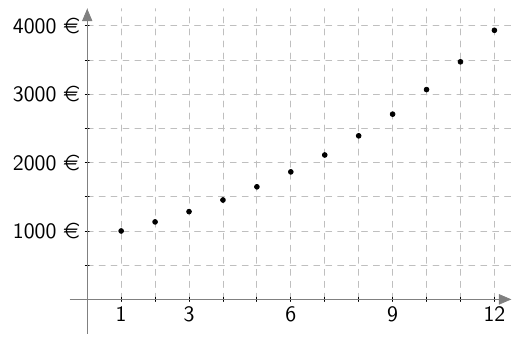
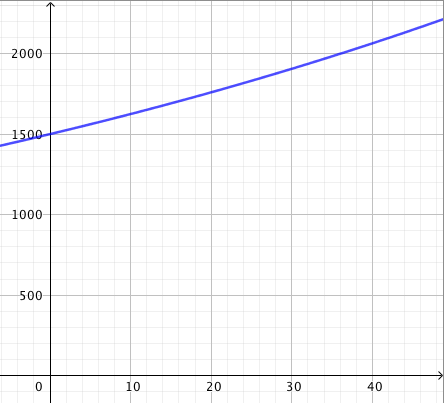
Kuvaaja ilmaisee 1500 metrin juoksukisan voittajan juokseman matkan ajan funktiona. Voittoaika oli 3:52,5.
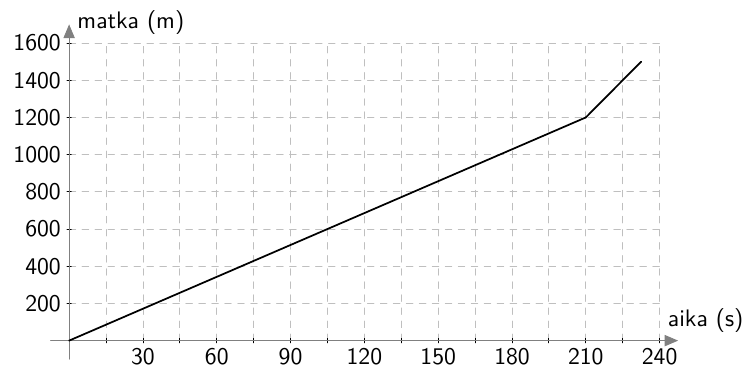
- Kuinka kauan aikaa voittaja käytti kilpailun ensimmäiseen 600 metriin?
- Kuinka monta metriä sekunnissa oli voittajan juoksunopeus kilpailun ensimmäisen 3,5 minuutin aikana? Miten tämä liittyy suoran kulmakertoimeen?
- Mitä tapahtui, kun oli juostu 1200 m?
- Mikä oli voittajan juoksunopeus viimeisten 22,5 sekunnin aikana?
- Voittaja käytti ensimmäiseen 600 metriin 105 sekuntia eli yhden minuutin ja 45 sekuntia; siis 1:45. Tämä nähdään siitä, että kuvaaja kulkee pisteen $(105, 600)$ kautta.
- Juoksunopeus oli $$ k = \dfrac{1200 \text{ m}}{210 \text{ s}} \approx 5{,}7 \text{ m/s}. $$ Tämä on sama kuin kuvaajan loivemman osan kulmakerroin.
- Juoksuvauhti kasvoi eli alkoi loppukiri.
- Juoksunopeus oli $$ k = \dfrac{300 \text{ m}}{22{,}5 \text{ s}} \approx 13{,}3 \text{ m/s}. $$
Suoran yhtälön muodostamista varten tarvitaan suoran kulmakerroin $k$ ja tieto siitä, millä korkeudella suora leikkaa $y$-akselin. Tämä korkeus on sama kuin suoran yhtälössä $y = kx + b$ esiintyvä vakio $b$.
Tehtävänä on määrittää yhtälö alla näkyvälle suoralle.
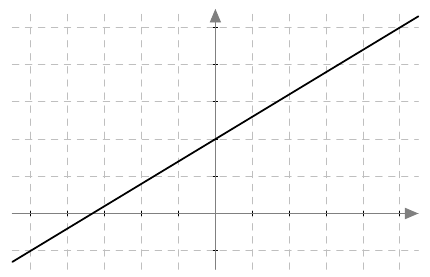
- Määritä suoran kulmakerroin $k$.
- Millä korkeudella suora leikkaa $y$-akselin eli mikä on vakio $b$?
- Mikä on suoran yhtälö?
- $k = \dfrac{3}{5} = 0{,}6$
- $b = 2$
- $y = \dfrac{3}{5}x + 2$
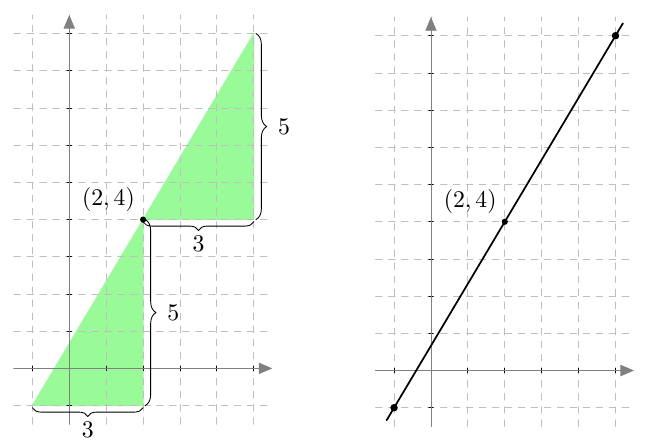
Suoran ja $y$-akselin tarkkaa leikkauspistettä ei välttämättä pysty lukemaan kuvasta. Tällaisessa tilanteessa riittää, että kulmakertoimen lisäksi tunnetaan jokin piste, jonka kautta suora kulkee. Tarkastellaan esimerkiksi tilannetta, jossa tiedetään, että suora kulkee pisteen $(2,4)$ kautta ja sen kulmakerroin on $$ k = \dfrac{5}{3}. $$ Tällöin tiedetään, että suoran yhtälö on muotoa $$ y = \dfrac{5}{3}x + b. $$ Koska suora kulkee pisteen $(2,4)$ kautta, sen koordinaatit toteuttavat suoran yhtälön. Saadaan siis yhtälö $$ 4 = \dfrac{5}{3} \cdot 2 + b, $$ jossa ainoa tuntematon on $b$. Yhtälöä voidaan ensin sieventää laskemalla kertolasku, jolloin yhtälö saadaan muotoon $$ 4 = \dfrac{10}{3} + b. $$ Vakio $b$ saadaan selville, kun yhtälön molemmilta puolilta vähennetään $10/3$. Tällöin oikealle puolelle jää pelkkä $b$: $$ 4 - \dfrac{10}{3} = b. $$ Vakion $b$ arvo voidaan nyt sieventää laskimella tai käsin: \begin{align*} b &= 4 - \dfrac{10}{3} \\[2mm] &= \dfrac{4 \cdot 3}{3} - \dfrac{10}{3} \\[2mm] &= \dfrac{12}{3} - \dfrac{10}{3} = \dfrac{2}{3}. \end{align*} Suoran yhtälö on siis $$ y = \dfrac{5}{3}x + \dfrac{2}{3}. $$ Alla olevassa kuvassa on havainnollistettu tapaa, jolla suora voidaan piirtää koordinaatistoon, jos tunnetaan suoran kulmakerroin ja yksi suoran piste. Tunnetusta pisteestä $(2,4)$ lähtien voidaan löytää muita suoran pisteitä, kun muistetaan, että kulmakerroin $5/3$ tarkoittaa, että aina kun siirrytään 3 ruutua oikealle, suora nousee 5 ruutua ylöspäin.
Tiedetään, että suora kulkee pisteen $(1,2)$ kautta ja sen kulmakerroin on $$ k = -\dfrac{3}{2}. $$
- Piirrä suora koordinaatistoon.
- Sijoita tunnetun pisteen koordinaatit ja kulmakertoimen arvo suoran yhtälöön $$ y = kx + b $$ ja ratkaise vakion $b$ arvo.
- Mikä on suoran yhtälö?
- Kulmakerroin on negatiivinen, joten suora on laskeva. Suoran piirtäminen:
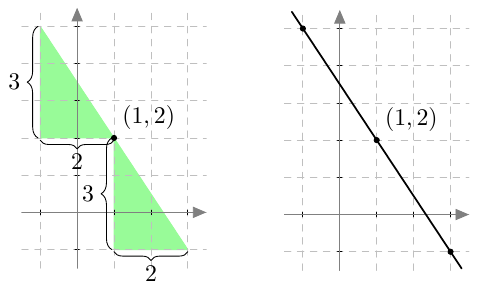
- $b = \dfrac{7}{2}$
Vakio $b$ saadaan ratkaistua yhtälöstä $$ 2 = -\dfrac{3}{2} \cdot 1 + b. $$ - $y = -\dfrac{3}{2}x + \dfrac{7}{2}$
Suoran yhtälö voidaan määrittää myös tilanteessa, jossa tunnetaan kaksi suoran pistettä. Niiden avulla saadaan selville suoran kulmakerroin $k$ ja sen jälkeen vakion $b$ arvo voidaan selvittää kuten edellä tehtiin.
Suora kulkee pisteiden $(-2,3)$ ja $(3,1)$ kautta. Tehtävänä on määritää suoran yhtälö.
- Merkitse suoran pisteet koordinaatistoon ja laske suoran kulmakerroin. Varmista piirroksesi avulla, että tulos on järkevä.
- Sijoita jomman kumman tunnetun pisteen koordinaatit ja kulmakertoimen arvo suoran yhtälöön $$ y = kx + b $$ ja ratkaise vakion $b$ arvo.
- Mikä on suoran yhtälö?
- Kulmakerroin on $$ k = -\dfrac{2}{5} = -0{,}4. $$
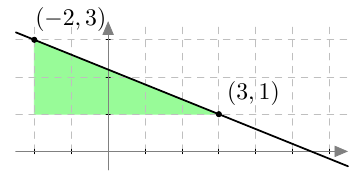
- $b = \dfrac{11}{5} = 2{,}2$
- $y = -\dfrac{2}{5}x + \dfrac{11}{5}$
Koordinaatiston minkä tahansa kahden pisteen kautta voidaan piirtää suora. Joskus voi käydä niin, että valituilla pisteillä on sama $y$-koordinaatti tai sama $x$-koordinaatti. Seuraavassa tehtävässä tutkitaan, millainen yhtälö on suoralla, jonka pisteillä on sama $y$-koordinaatti.
Suora kulkee pisteiden $(-3,2)$ ja $(4,2)$ kautta. Tehtävänä on määritää suoran yhtälö.
- Merkitse suoran pisteet koordinaatistoon ja laske suoran kulmakerroin. Varmista piirroksesi avulla, että tulos on järkevä.
- Sijoita jomman kumman tunnetun pisteen koordinaatit ja kulmakertoimen arvo suoran yhtälöön $$ y = kx + b $$ ja ratkaise vakion $b$ arvo.
- Mikä on suoran yhtälö?
- Kulmakerroin on $$ k = \dfrac{2-2}{4-(-3)} = \dfrac{0}{7} = 0. $$
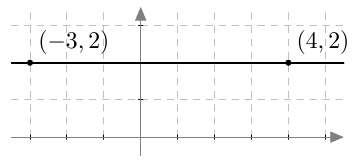
- $b = 2$
- $y = 2$
Edellisestä tehtävästä havaitaan, että jos suoran pisteillä on sama $y$-koordinaatti, suoran kulmakerroin on nolla ja suoran yhtälö on muotoa $y = b$. Suora on $x$-akselin suuntainen ja leikkaa $y$-akselin korkeudella $b$. Tällainen suora on vakiofunktion $f(x) = b$ kuvaaja.
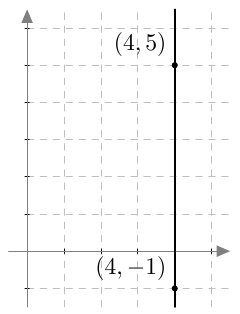
Jos suoran pisteillä on sama $x$-koordinaatti, suoran kulmakerrointa ei voi määrittää, koska kulmakertoimen lausekkeessa jakajaan tulisi nolla. Suora on tässä tapauksessa $y$-akselin suuntainen ja sen yhtälö on muotoa $x = a$. Esimerkiksi pisteiden $(4,-1)$ ja $(4,5)$ kautta kulkevan suoran yhtälö on $x = 4$:
Nämä havainnot voidaan osoittaa yleispäteviksi, joten kootaan ne seuraavaan teoreemaan:
TEOREEMA
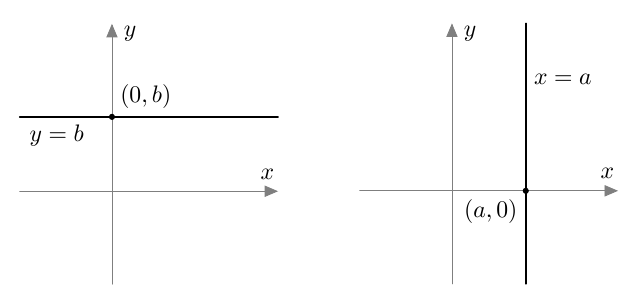
Jos suora on $x$-akselin suuntainen, sen kulmakerroin on nolla ja suoran yhtälö on muotoa $$ y = b, $$ missä $b$ on jokin luku.
Jos suora on $y$-akselin suuntainen, sen yhtälö on muotoa $$ x = a, $$ missä $a$ on jokin luku.
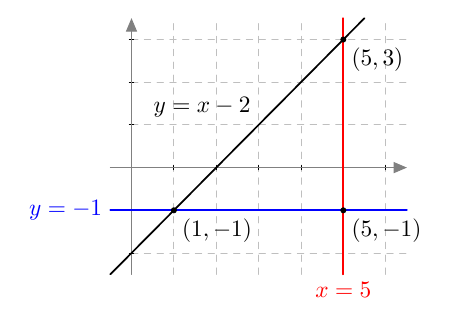
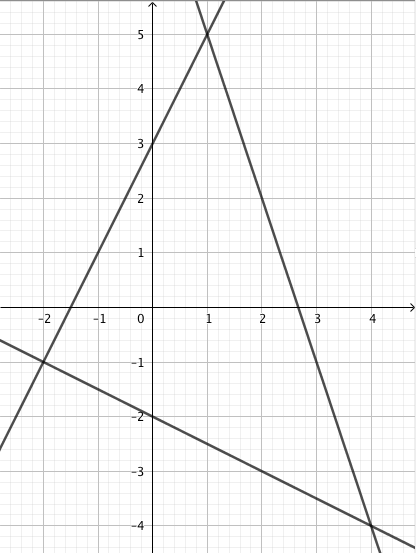
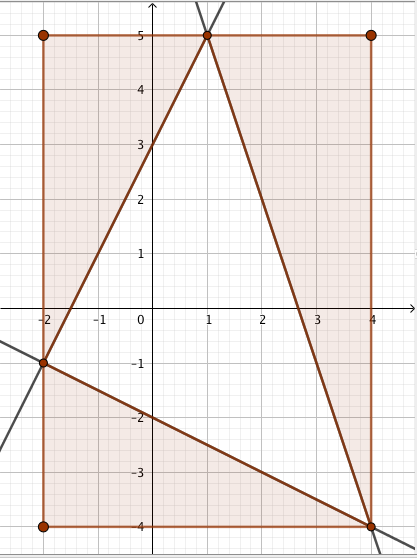
Kolmion kärjet ovat pisteissä $(1,-1)$; $(5,-1)$ ja $(5,3)$. Jos kolmion sivuja jatketaan, muodostuu kolme suoraa.
- Piirrä tilanteesta kuva.
- Mitkä ovat syntyvien kolmen suoran yhtälöt?
Kuva ja suorien yhtälöt: