MAA7 - Trigonometriset funktiot
Kurssin tavoitteet ja keskeiset sisällöt
Kurssin tavoitteena on, että
- tutkit trigonometrisia funktioita yksikköympyrän symmetrioiden avulla
- osaat ratkaista sellaisia trigonometrisia yhtälöitä, jotka ovat tyyppiä $\sin f(x) = a$ tai $\sin f(x) = \sin g(x)$
- tunnet trigonometristen funktioiden yhteydet $\sin^2 x + \cos^2 x = 1$ ja $$\tan x = \dfrac{\sin x}{\cos x}$$
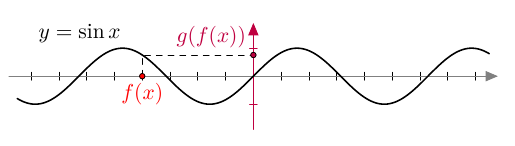
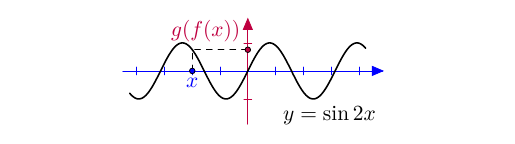
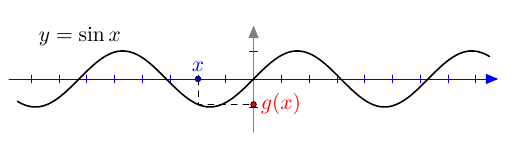
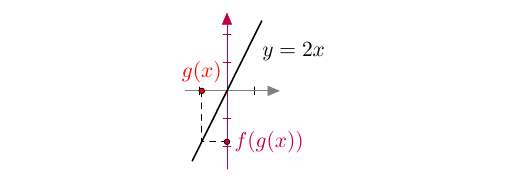
- osaat derivoida yhdistettyjä funktioita
- osaat tutkia trigonometrisia funktioita derivaatan avulla
- osaat hyödyntää trigonometrisia funktioita mallintaessasi jaksollisia ilmiöitä
- osaat käyttää teknisiä apuvälineitä trigonometristen funktioiden tutkimisessa, trigonometristen yhtälöiden ratkaisemisessa ja trigonometristen funktioiden derivaattojen määrittämisessä sovellusongelmissa.
Keskeiset sisällöt
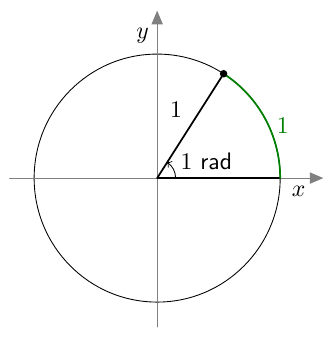
- suunnattu kulma ja radiaani
- trigonometriset funktiot symmetria- ja jaksollisuusominaisuuksineen
- trigonometristen yhtälöiden ratkaiseminen
- yhdistetyn funktion derivaatta
- trigonometristen funktioiden derivaatat.
Opiskeluohjeita
Kurssimateriaali on jaettu kolmeen lukuun: Trigonometriaa yksikköympyrässä, Trigonometriset funktiot ja Yhdistetty funktio.
Pääajatus kurssimateriaalissa on, että matematiikkaa oppii parhaiten tekemällä matematiikkaa. Materiaali on tämän vuoksi kirjoitettu niin, että teet tehtäviä käytännössä koko ajan. Jokainen luku sisältää kolme eri tehtäväsarjaa. Ensimmäisen tehtäväsarjan tehtävät ovat teorian seassa. Tarkoitus on, että etenet materiaalissa tekemällä jokaisen näistä tehtävistä. Voit hyvin tehdä tehtäviä yhdessä kaverin kanssa ja voit kysyä opettajalta heti, jos et ymmärrä jotain asiaa. Asia voi olla jokin tietty tehtävä, teoriassa oleva virke tai esimerkiksi vieras matemaattinen symboli. Pääasia on, että sinä itse teet tehtävät ja ymmärrät, mitä teet. Tämän tehtäväsarjan jälkeen kyseisen luvun teoria on käsitelty ja on aika harjoitella ja syventää juuri opittua. Ennen tätä opettaja pitää ehkä yhteisen opetustuokion tai -keskustelun, jossa pohditaan yhdessä luvun keskeisiä asioita tai työskentelyssä esiin tulleita haastavia kohtia. Mahdollisen opetustuokion jälkeen jatka harjoittelua luvun lopussa olevien kahden tehtäväsarjan tehtävien avulla. Luonnollisesti mitä enemmän harjoittelet, sitä paremmaksi tulet. Kun olet valmis, tee luvun lopussa oleva(t) itsearviointitesti(t). Niiden tarkoitus on kertoa sinulle, oletko ymmärtänyt luvun olennaiset asiat ja kehittää samalla oman oppimisesi arviointia, joka on tärkeä tulevaisuuden taito. Testeissä pärjääminen ei vielä tarkoita, että osaat luvun asiat esimerkiksi kiitettävällä tasolla, vaan testit keskittyvät vahvan perusosaamisen tutkimiseen. Ennen siirtymistä seuraavaan lukuun opettaja haluaa ehkä vielä koota luvussa opittuja asioita sekä antaa palautetta oppimisesta ja sen etenemisestä yhteisessä opetuskeskustelussa.

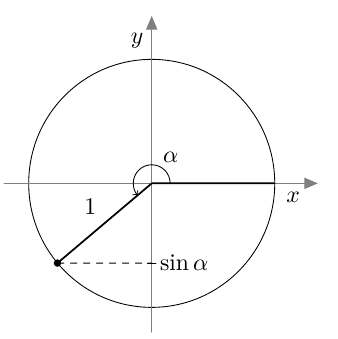
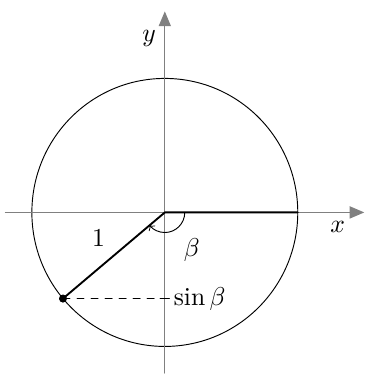
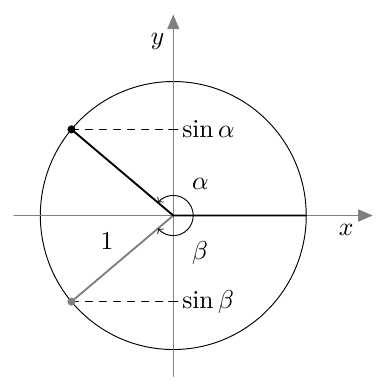
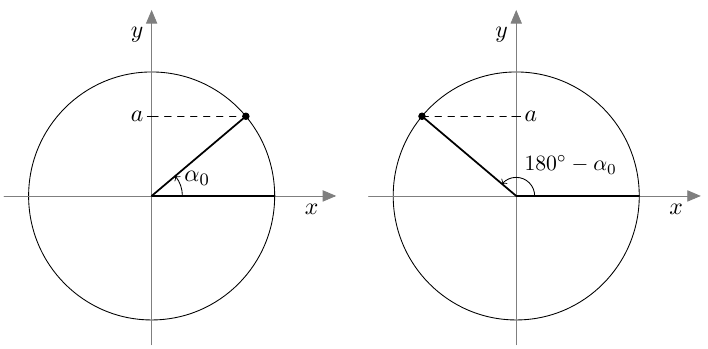
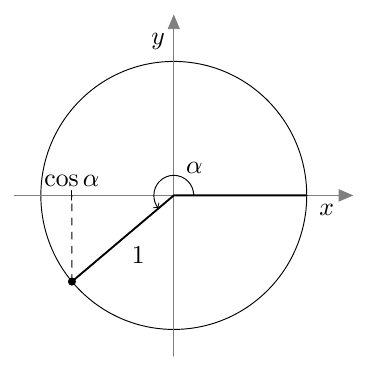
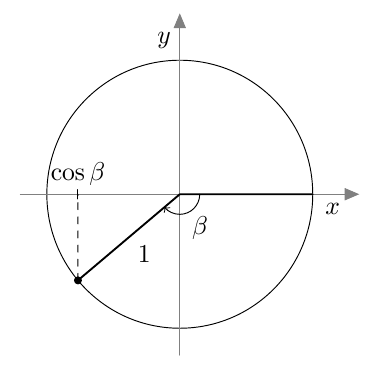
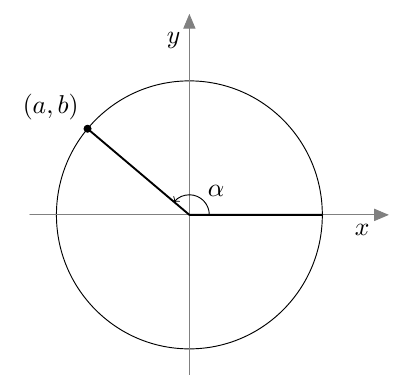
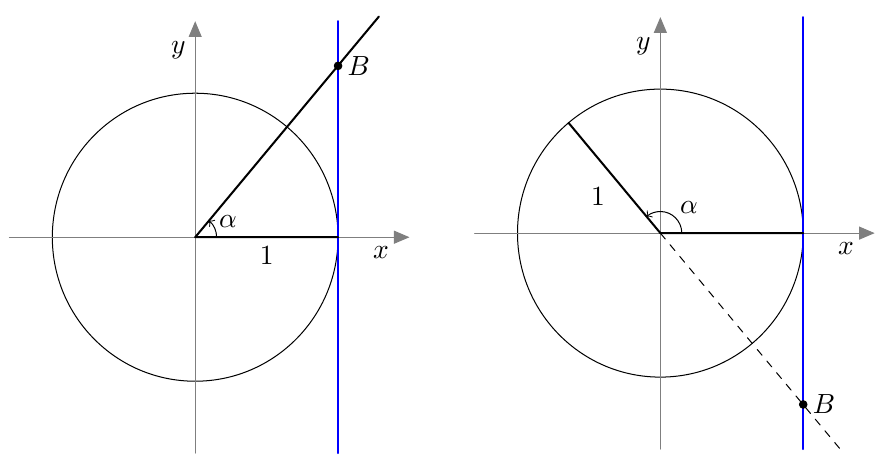
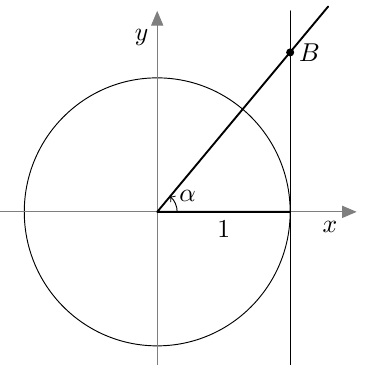
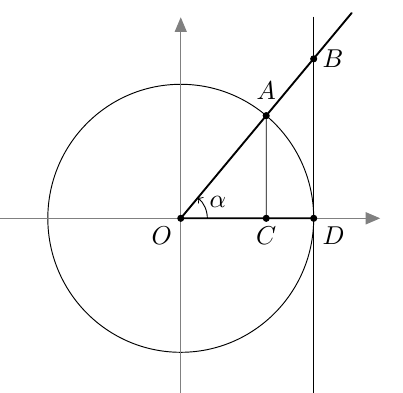
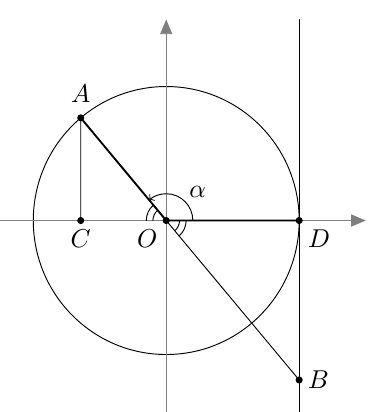
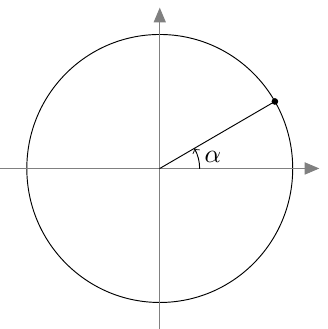
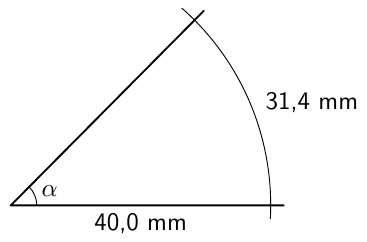
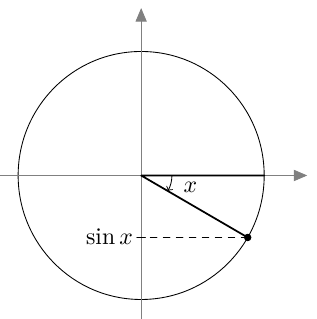
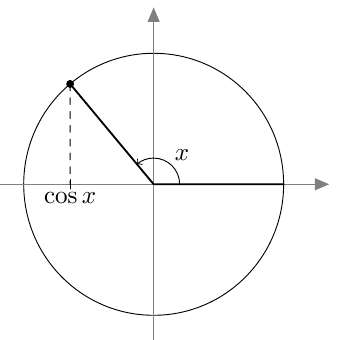
 Myöhemmin samalla kurssilla otettiin käyttöön uusi määritelmä, joka kattaa myös tylppäkulmaiset kolmiot. Jos $0^\circ \leq \alpha \leq 180^\circ$, määritellään kulman $\alpha$ sini seuraavasti: Piirretään origosta lähtevä jana, jonka pituus on 1 ja joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$. Kulman $\alpha$ sini on tämän janan toisen päätepisteen $y$-koordinaatti:
Myöhemmin samalla kurssilla otettiin käyttöön uusi määritelmä, joka kattaa myös tylppäkulmaiset kolmiot. Jos $0^\circ \leq \alpha \leq 180^\circ$, määritellään kulman $\alpha$ sini seuraavasti: Piirretään origosta lähtevä jana, jonka pituus on 1 ja joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$. Kulman $\alpha$ sini on tämän janan toisen päätepisteen $y$-koordinaatti: 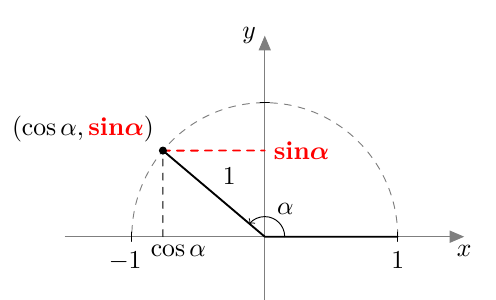
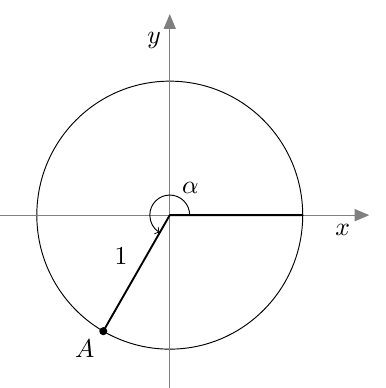
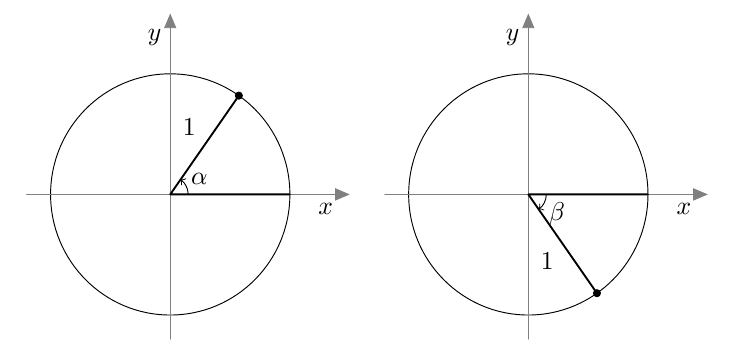
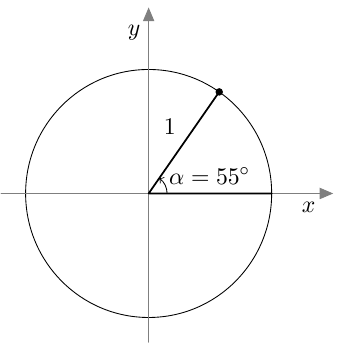
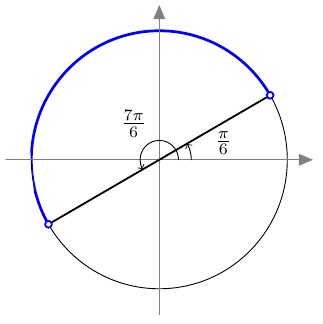
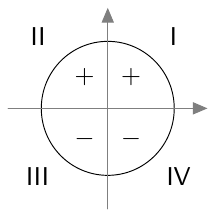
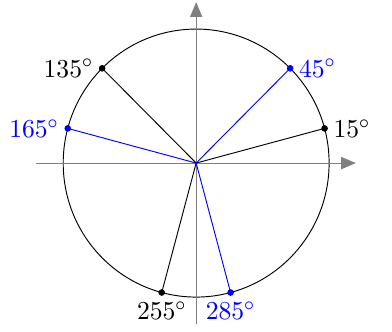
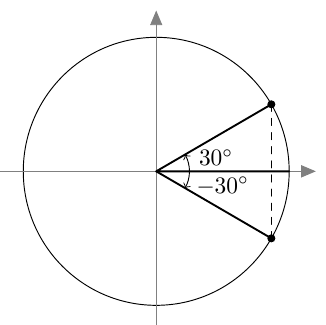
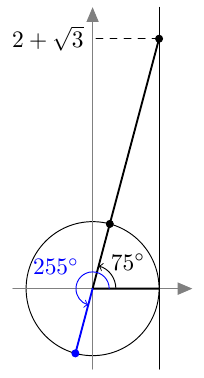
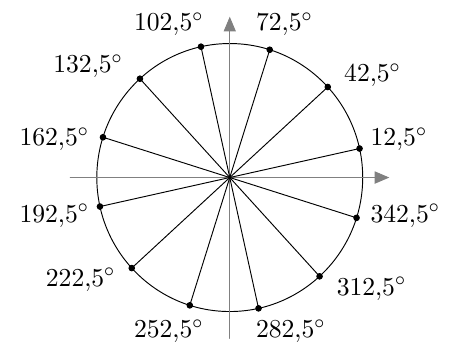
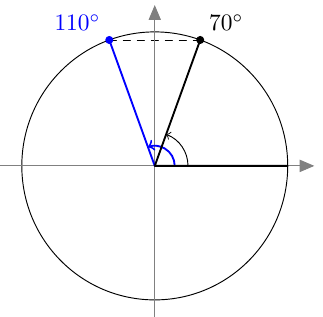
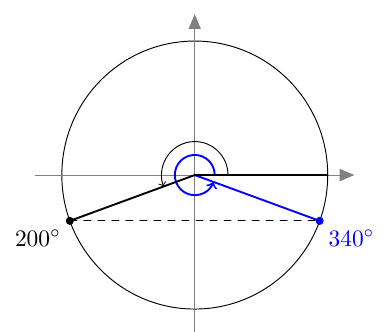
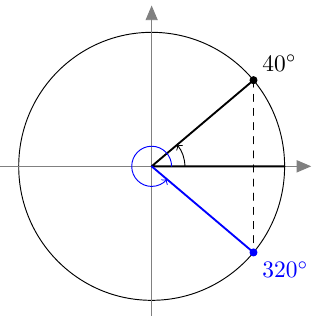
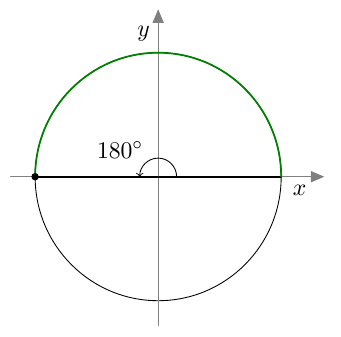
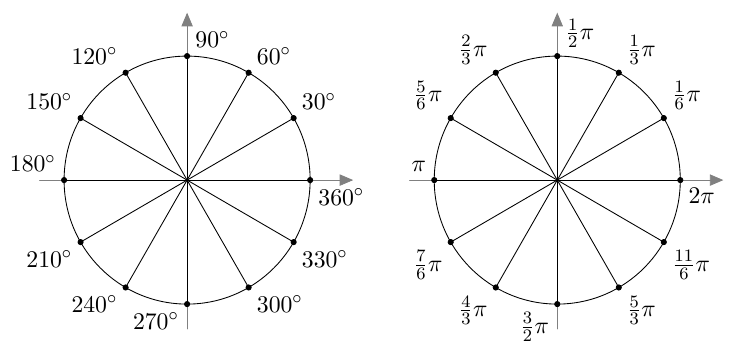
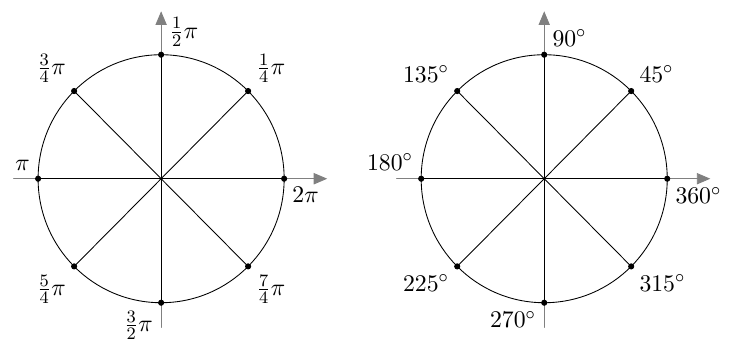
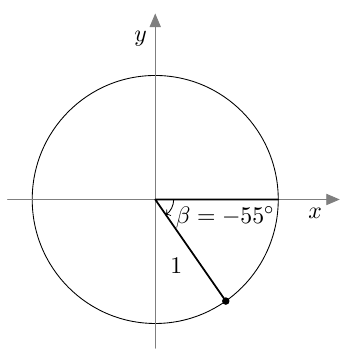 Suunnattu kulma merkitään koordinaatistoon niin, että sen alkukylki on positiivisella $x$-akselilla. Kierron suuruus määrää, mihin suunnatun kulman loppukylki asettuu.
Suunnattu kulma merkitään koordinaatistoon niin, että sen alkukylki on positiivisella $x$-akselilla. Kierron suuruus määrää, mihin suunnatun kulman loppukylki asettuu. 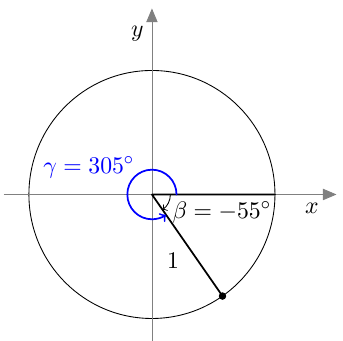
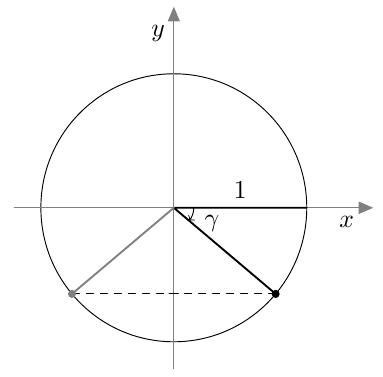
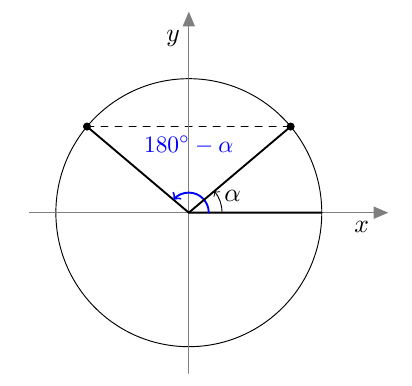
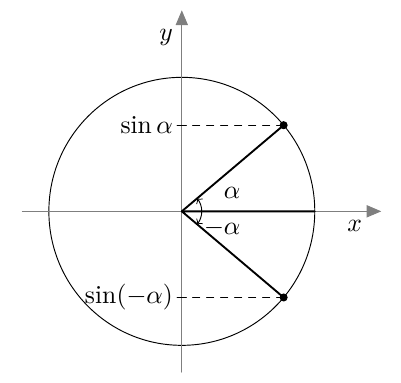
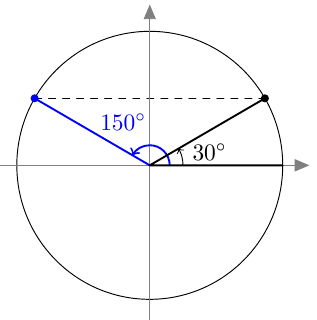
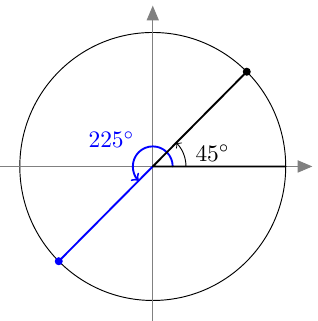
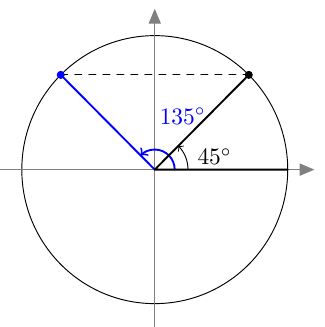
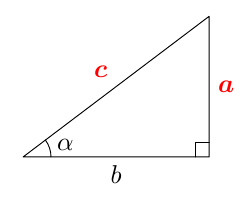
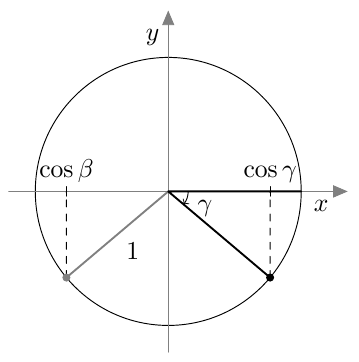
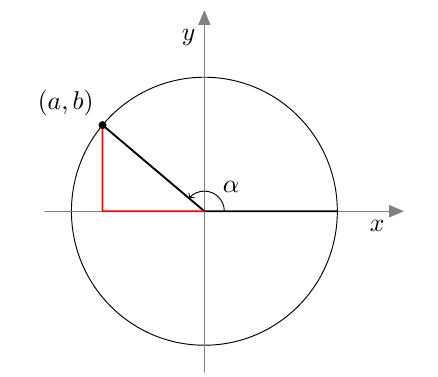
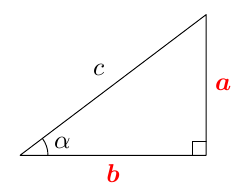
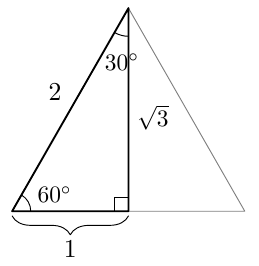
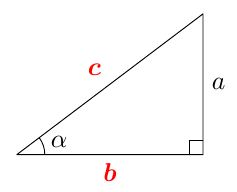 Tästä juontaa juurensa myös kosinin nimi. Kulman $\alpha$ kosini on nimittäin kolmion toisen terävän kulman, ns. komplementtikulman sini: \begin{align*} \cos \alpha &= \textcolor{red}{\dfrac{\boldsymbol{b}}{\boldsymbol{c}}} = \sin (90^\circ - \alpha). \end{align*} Kosini muistuttaa monilta ominaisuuksiltaan siniä. Kun opiskelet tätä kappaletta, pidä mielessä edellisen kappaleen asiat ja kokeile, pystytkö jo ennalta arvaamaan kosinin uuden määritelmän ja siitä seuraavat kosinin ominaisuudet.
Tästä juontaa juurensa myös kosinin nimi. Kulman $\alpha$ kosini on nimittäin kolmion toisen terävän kulman, ns. komplementtikulman sini: \begin{align*} \cos \alpha &= \textcolor{red}{\dfrac{\boldsymbol{b}}{\boldsymbol{c}}} = \sin (90^\circ - \alpha). \end{align*} Kosini muistuttaa monilta ominaisuuksiltaan siniä. Kun opiskelet tätä kappaletta, pidä mielessä edellisen kappaleen asiat ja kokeile, pystytkö jo ennalta arvaamaan kosinin uuden määritelmän ja siitä seuraavat kosinin ominaisuudet. 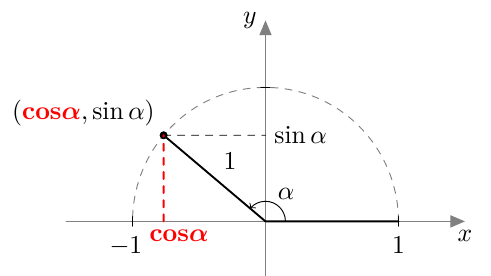
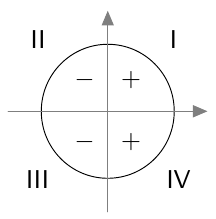
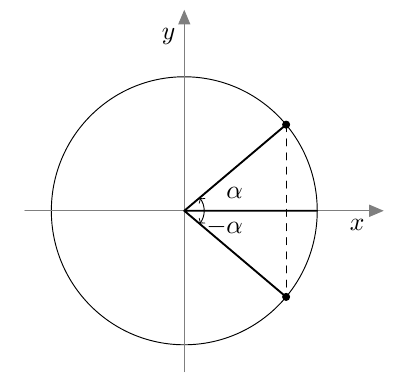
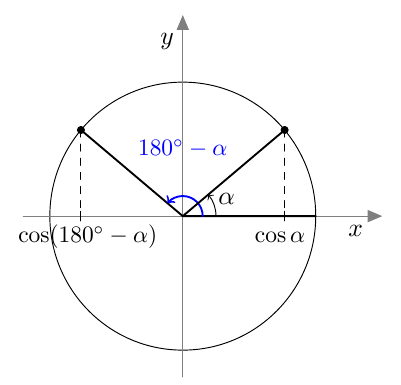
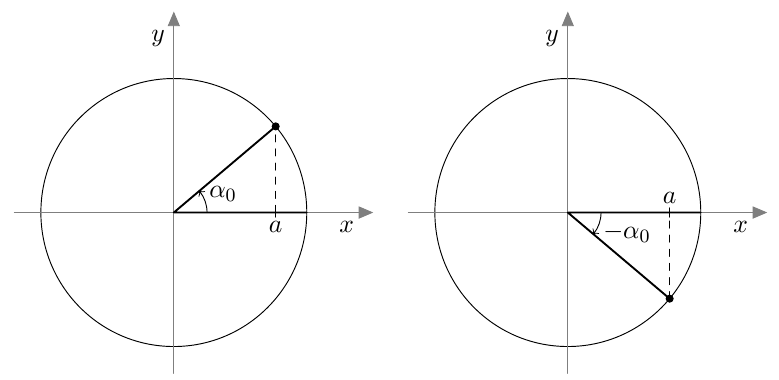
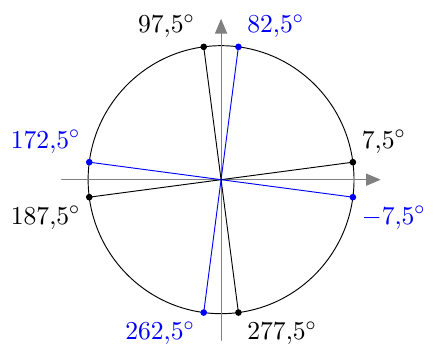

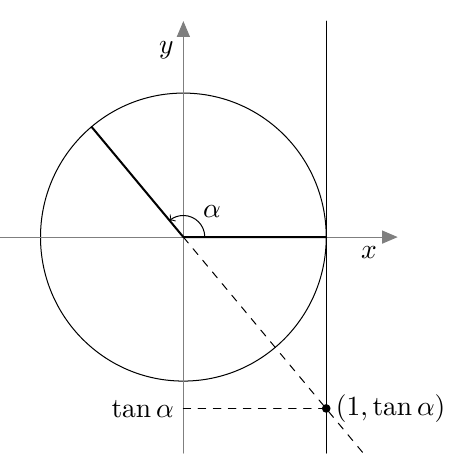
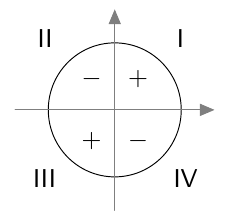
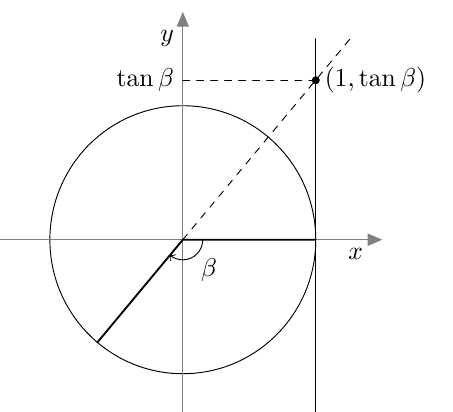
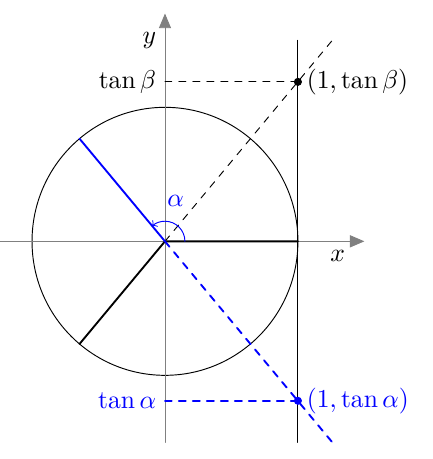
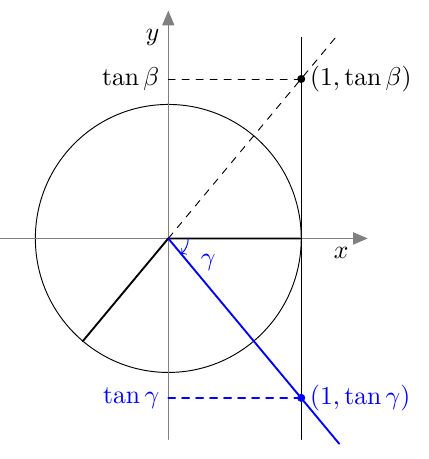
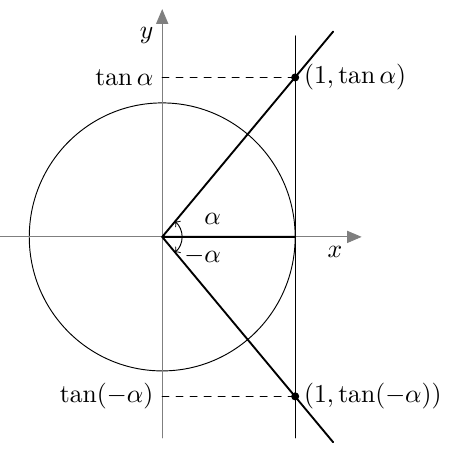
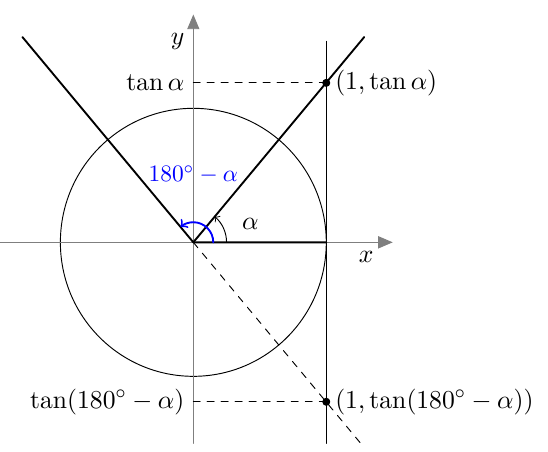
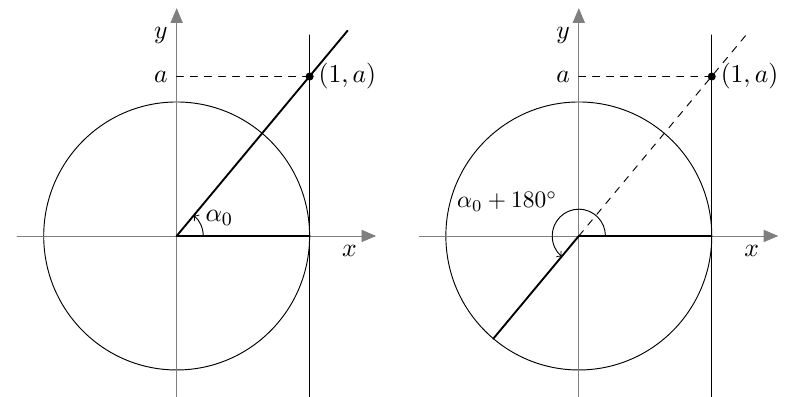
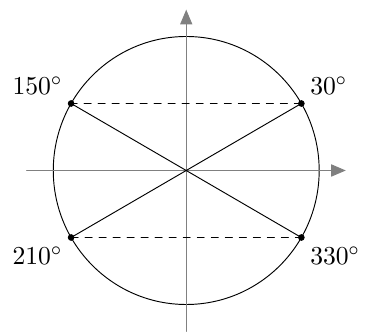
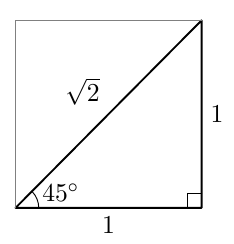
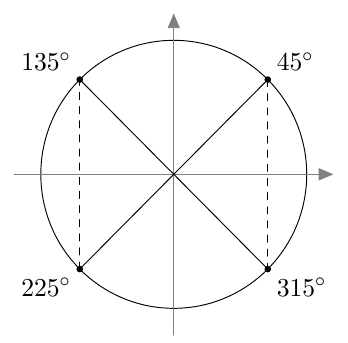
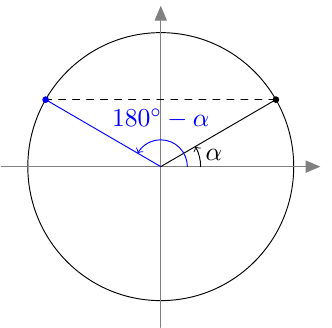
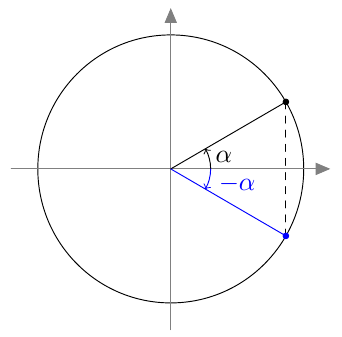
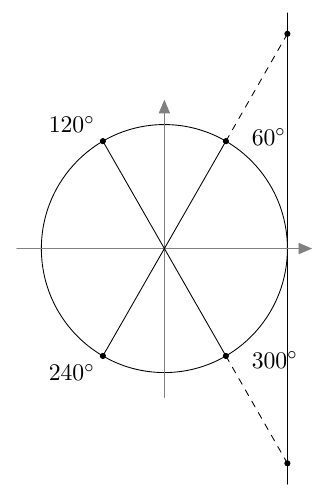

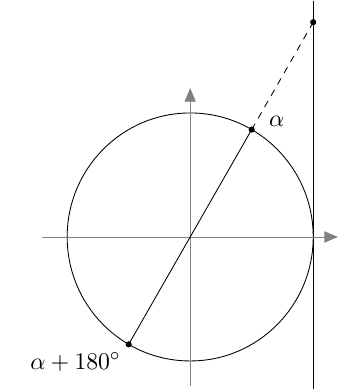

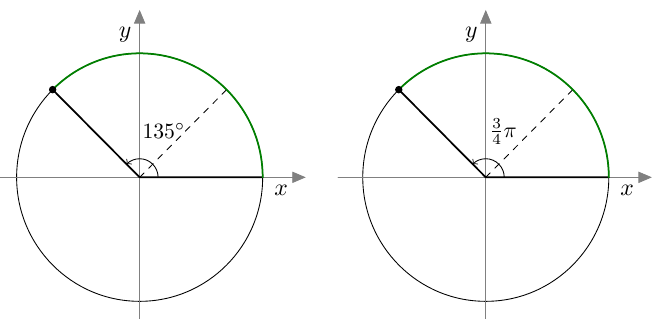
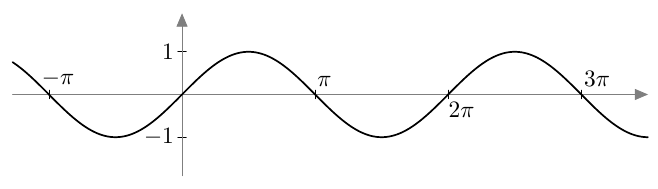

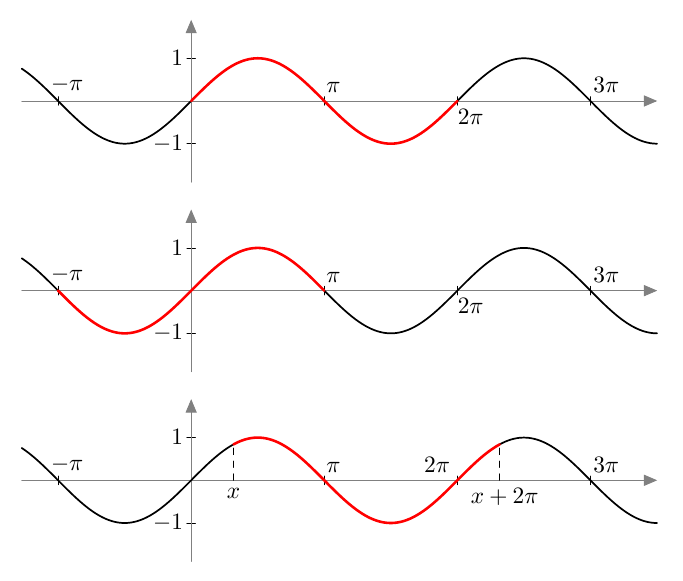
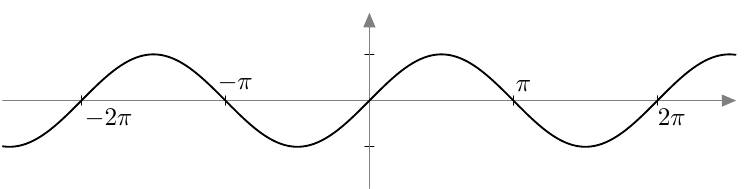
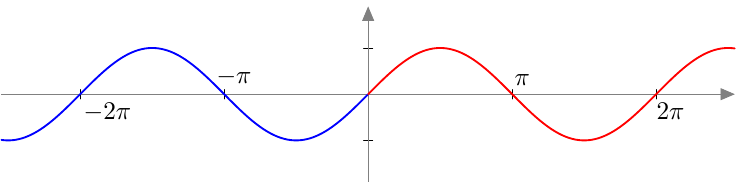
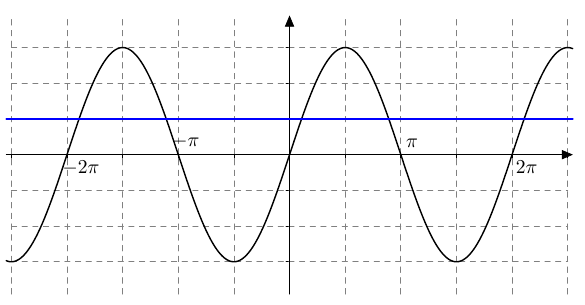
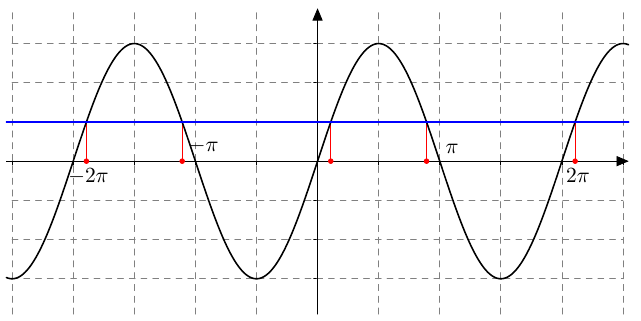
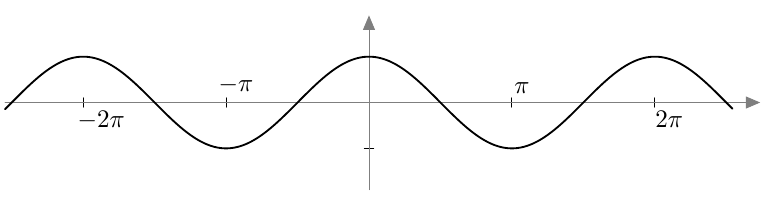
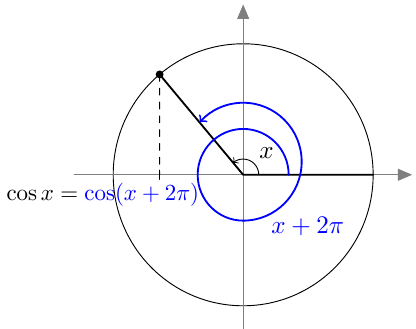
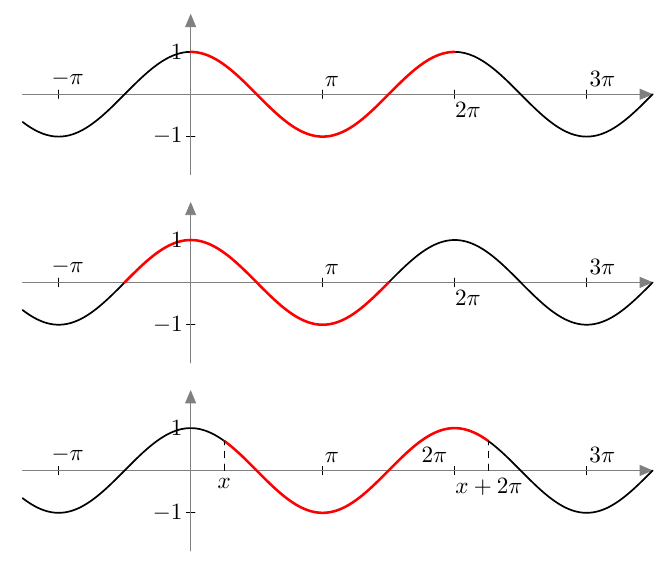
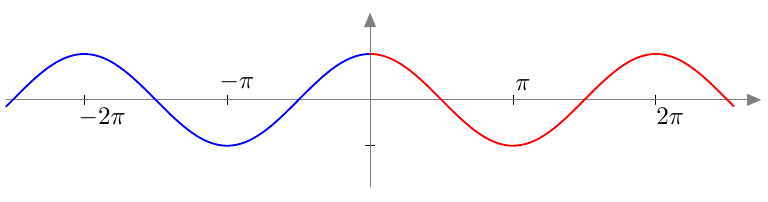
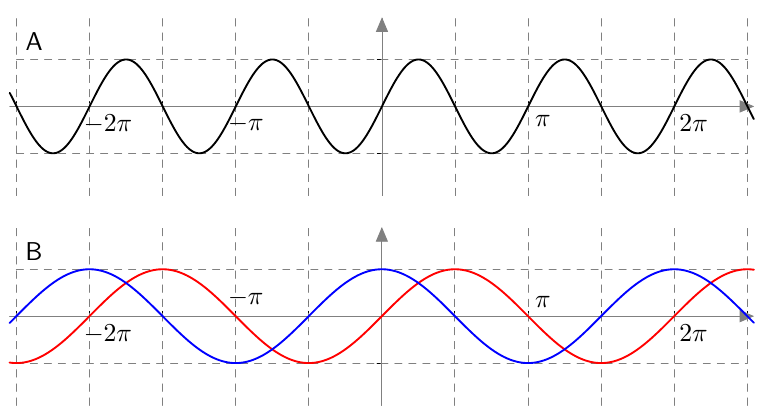
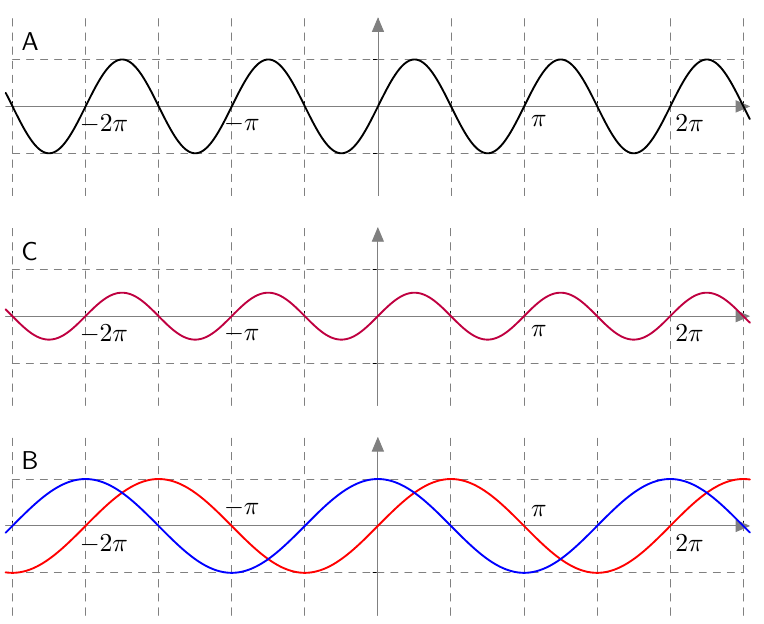
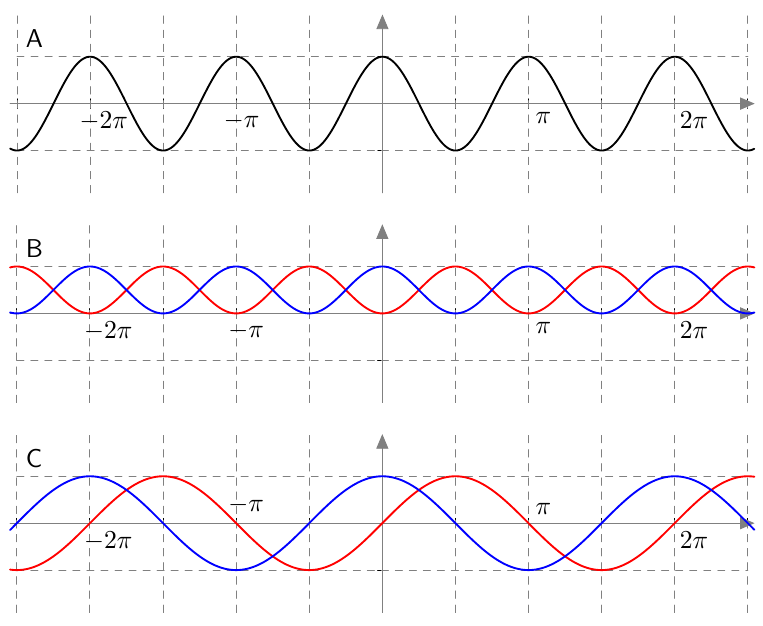
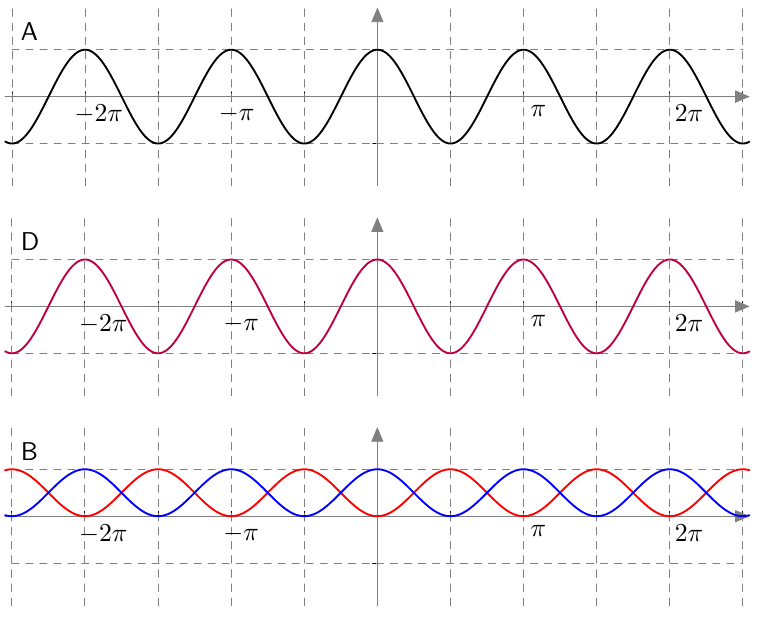
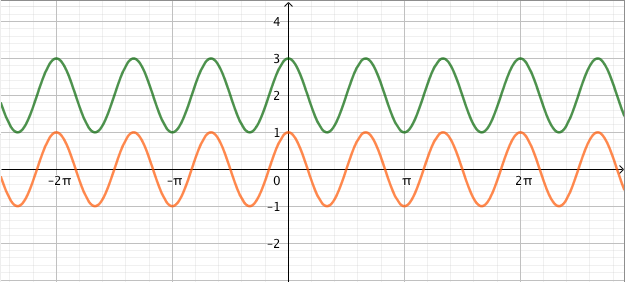
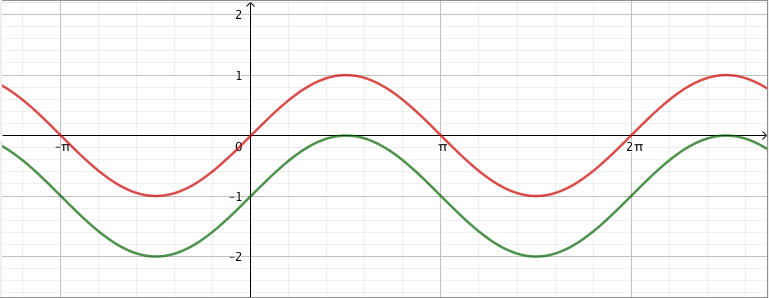
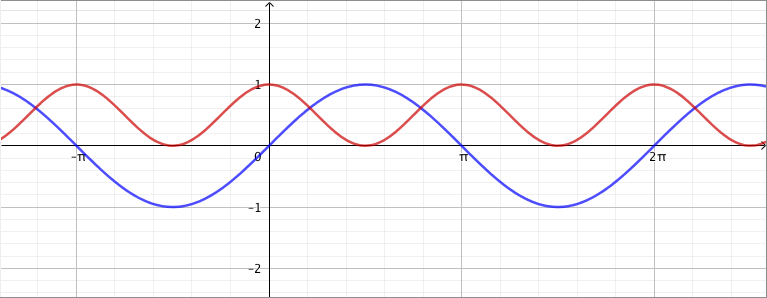
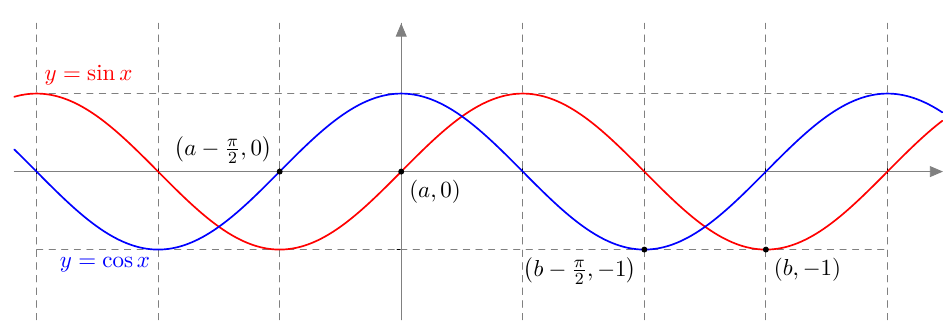 Vastaavasti sinifunktio saa kaikki arvot $\frac{\pi}{2}$ verran kosinifunktion jälkeen:
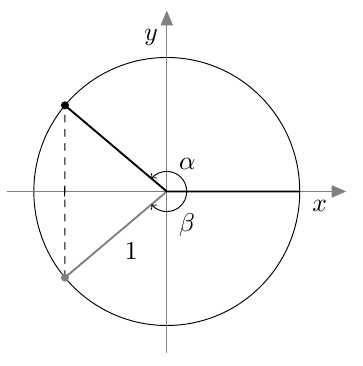
Vastaavasti sinifunktio saa kaikki arvot $\frac{\pi}{2}$ verran kosinifunktion jälkeen: 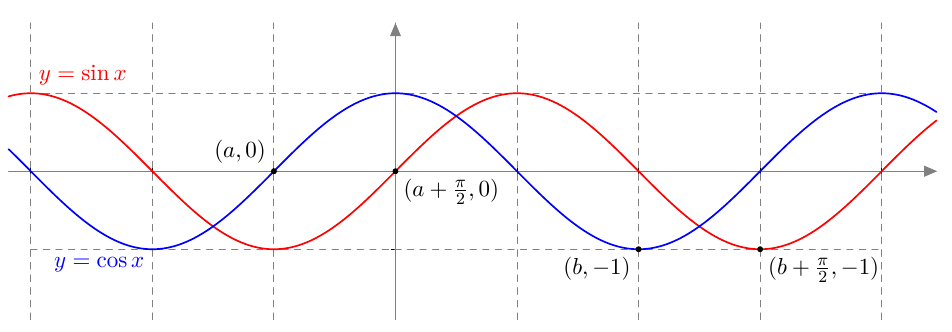 Sinifunktion ja kosinifunktion niin sanottu vaihe-ero on siis $\frac{\pi}{2}$ eli neljäsosa niiden jakson pituudesta.
Sinifunktion ja kosinifunktion niin sanottu vaihe-ero on siis $\frac{\pi}{2}$ eli neljäsosa niiden jakson pituudesta.