Trigonometriaa yksikköympyrässä
Luvun tavoitteet
Tämän luvun tavoitteena on, että saat vahvan visuaalisen mielikuvan sinistä, kosinista ja tangentista yksikköympyrässä. Osaat
- merkitä suunnatun kulman yksikköympyrään ja määrittää graafisesti likiarvot kulman sinille, kosinille ja tangentille
- merkitä yksikköympyrään kulmat, joilla on sama sini, kosini tai tangentti kuin annetulla kulmalla $\alpha$
- käyttää yksikköympyrää sinin, kosinin ja tangentin tarkkojen arvojen ja merkin määrittämiseen
- määrittää trigonometristen yhtälöiden kaikki ratkaisut yksikköympyrän avulla.
Sini
Tässä kappaleessa yleistetään kulman sinin käsite kaikille suunnatuille kulmille, tutkitaan sinin ominaisuuksia ja opitaan ratkaisemaan erilaisia siniyhtälöitä yksikköympyrän avulla. Aloitetaan palauttamalla mieleen kulman sinin aikaisempia määritelmiä.
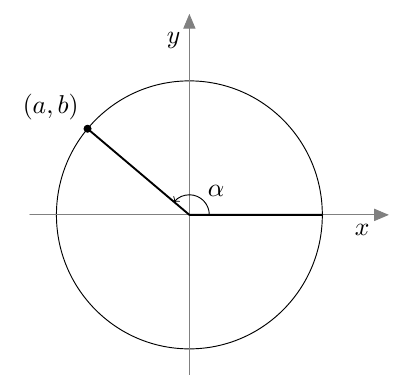
Kurssilla MAA3 kulman sini määriteltiin aluksi suorakulmaisen kolmion avulla: Suorakulmaisessa kolmiossa terävän kulman $\alpha$ sini tarkoittaa kulman vastaisen kateetin suhdetta hypoteenuusaan. Alla olevan kuvion merkinnöillä \begin{align*} \sin \alpha &= \textcolor{red}{\dfrac{\boldsymbol{a}}{\boldsymbol{c}}} \end{align*} 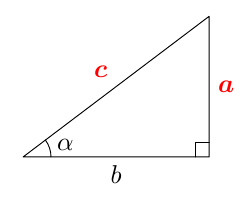 Myöhemmin samalla kurssilla otettiin käyttöön uusi määritelmä, joka kattaa myös tylppäkulmaiset kolmiot. Jos $0^\circ \leq \alpha \leq 180^\circ$, määritellään kulman $\alpha$ sini seuraavasti: Piirretään origosta lähtevä jana, jonka pituus on 1 ja joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$. Kulman $\alpha$ sini on tämän janan toisen päätepisteen $y$-koordinaatti:
Myöhemmin samalla kurssilla otettiin käyttöön uusi määritelmä, joka kattaa myös tylppäkulmaiset kolmiot. Jos $0^\circ \leq \alpha \leq 180^\circ$, määritellään kulman $\alpha$ sini seuraavasti: Piirretään origosta lähtevä jana, jonka pituus on 1 ja joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$. Kulman $\alpha$ sini on tämän janan toisen päätepisteen $y$-koordinaatti:
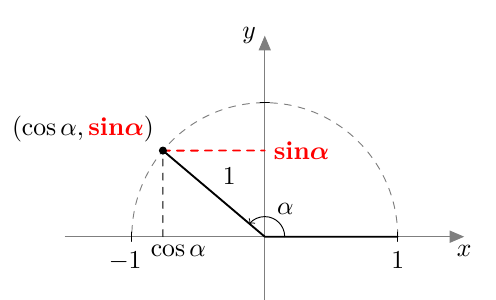
Kulman sini
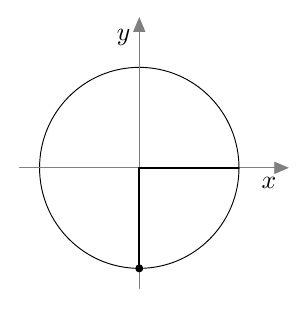
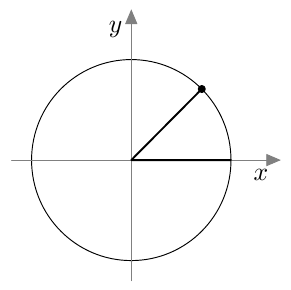
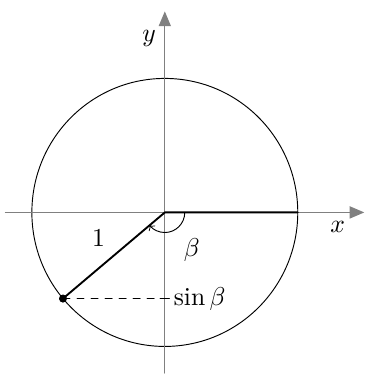
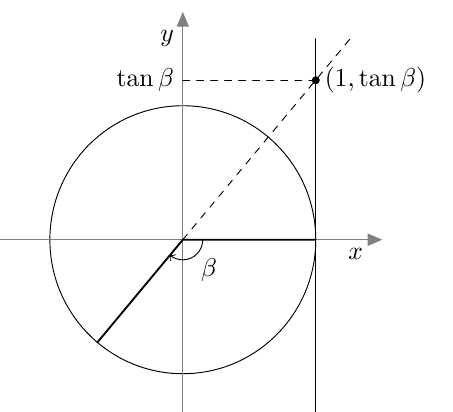
Tarkastele alla olevaa kuvaa.
- Määritä $\sin \beta$.
- Selvitä laskimella kulman $\beta$ suuruus. Anna vastaus kolmen merkitsevän numeron tarkkuudella. Kertaa tarvittaessa MAA3-kurssin tehtävä 1.20 ja sitä edeltävä teoriaosuus.
- Merkitse kulma $\beta$ koordinaatistoon ja päättele jokin toinen kulma, jolla on sama sinin arvo. Kertaa tarvittaessa MAA3-kurssin tehtävä 1.27.
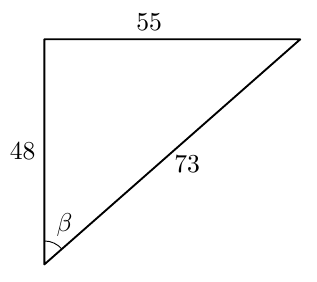
VASTAUS
- $\sin \beta = \dfrac{55}{73}$.
- $\beta \approx 48{,}9^\circ$
- Sopiva kulma on $180^\circ - 48{,}9^\circ = 131{,}1^\circ$.
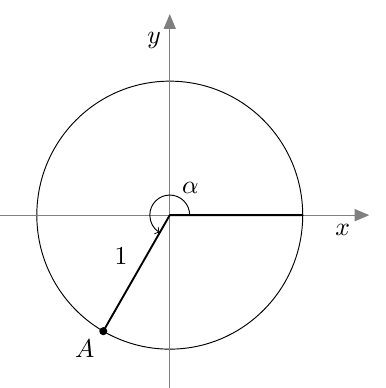
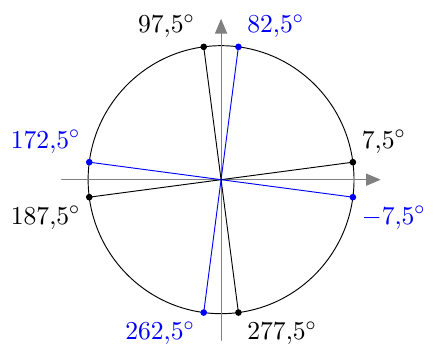
Mikä tahansa kulma voidaan sijoittaa koordinaatistoon niin, että kulman kärki on origossa ja kulman toinen kylki on positiivisella $x$-akselilla. Kulman toisen kyljen ja yksikköympyrän leikkauspistettä sanotaan kulman kehäpisteeksi:
MÄÄRITELMÄ: YKSIKKÖYMPYRÄ JA KULMAN KEHÄPISTE
Ympyrää, jonka keskipiste on origo ja säde 1, sanotaan yksikköympyräksi. Jos kulma $\alpha$ sijoitetaan koordinaatistoon niin, että sen kärki on origossa ja toinen kylki positiivisella $x$-akselilla, kulman $\alpha$ kehäpiste on kulman toisen kyljen ja yksikköympyrän leikkauspiste $A$:
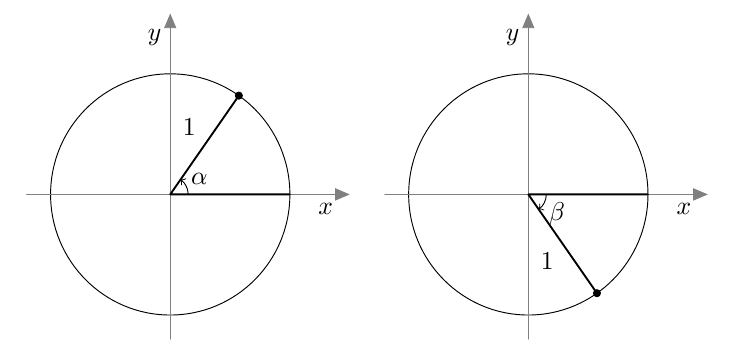
Yllä oleva määritelmä ei vielä riittävän tarkasti määrää, miten esimerkiksi $55^\circ$ kulma on sijoitettava koordinaatistoon. Alla on näkyvissä kaksi mahdollista tapaa, joissa molemmissa kulman kärki on origossa ja toinen kylki positiivisella $x$-akselilla:
Ongelma ratkaistaan ottamalla käyttöön suunnatun kulman käsite:
MÄÄRITELMÄ: SUUNNATTU KULMA
Suunnattu kulma ilmaisee kierron suunnan ja suuruuden. Kierto vastapäivään on positiivinen:
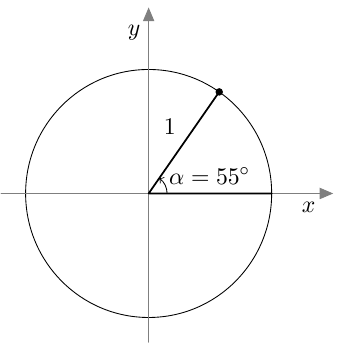
Kierto myötäpäivään on negatiivinen:
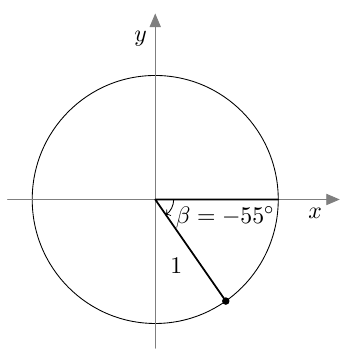 Suunnattu kulma merkitään koordinaatistoon niin, että sen alkukylki on positiivisella $x$-akselilla. Kierron suuruus määrää, mihin suunnatun kulman loppukylki asettuu.
Suunnattu kulma merkitään koordinaatistoon niin, että sen alkukylki on positiivisella $x$-akselilla. Kierron suuruus määrää, mihin suunnatun kulman loppukylki asettuu.
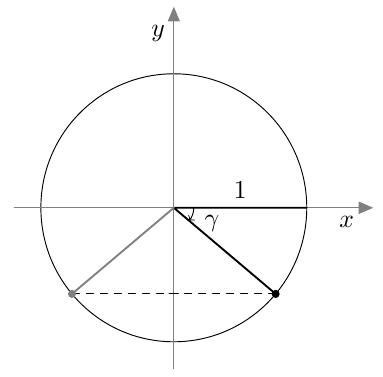
Monella eri kulmalla voi olla sama kehäpiste. Esimerkiksi alla olevassa kuvassa koordinaatistoon on merkitty kulmat $\beta$ ja $\gamma$, joilla on sama kehäpiste. Sama kehäpiste on esimerkiksi myös kulmalla $\alpha = 665^\circ$, joka saadaan kulmasta $\gamma$ lisäämällä yksi kierros eli täyskulma: $\alpha = \gamma + 360^\circ$.
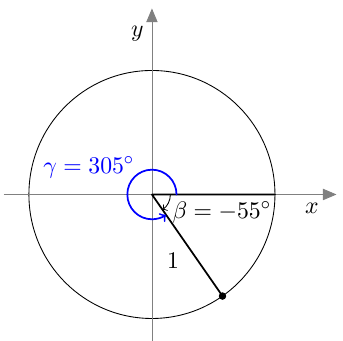
Kulman kehäpiste
Keksi neljä kulmaa, joilla on sama kehäpiste kuin alla olevissa kuvissa:
VASTAUS
- Esimerkiksi $-90^\circ$, $270^\circ$, $630^\circ$ ja $990^\circ$.
- Esimerkiksi $-315^\circ$, $45^\circ$, $405^\circ$ ja $765^\circ$.
- Esimerkiksi $-225^\circ$, $135^\circ$, $495^\circ$ ja $855^\circ$.
Kehäpisteen käsitteen avulla voimme nyt laajentaa sinin määritelmän kaikille suunnattuille kulmille:
MÄÄRITELMÄ: SUUNNATUN KULMAN SINI
Kulman $\alpha$ sini on kulman $\alpha$ kehäpisteen $y$-koordinaatti:
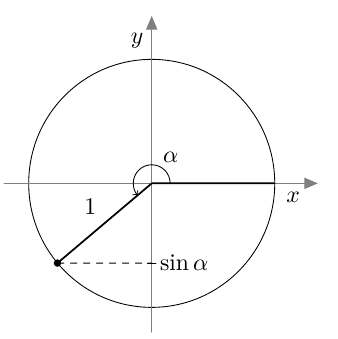
Suunnatun kulman sini
Määritä tämän Geogebra-havainnollistuksen avulla seuraavat sinin arvot kahden desimaalin tarkkuudella:
- $\sin 15^\circ$
- $\sin 120^\circ$
- $\sin 185^\circ$
- $\sin (-160^\circ )$
- $\sin (-55^\circ )$
VASTAUS
- $\sin 15^\circ \approx 0{,}26$
- $\sin 120^\circ \approx 0{,}87$
- $\sin 185^\circ \approx -0{,}09$
- $\sin (-160^\circ ) \approx -0{,}34$
- $\sin (-55^\circ ) \approx -0{,}82$
Seuraavissa tehtävissä tutkitaan sinin ominaisuuksia yksikköympyrän avulla.
Sinin arvot
Päättele vastaukset seuraaviin kysymyksiin. Voit käyttää apuna alla näkyvää yksikköympyrää tai tätä Geogebra-havainnollistusta.
- Mikä on suurin arvo, jonka kulman sini voi saada?
- Mikä on pienin arvo, jonka kulman sini voi saada?
- Onko sinin suurimman ja pienimmän arvon välillä jonkin arvo, jota sini ei koskaan saa? Selitä omin sanoin.

VASTAUS
- Sinin suurin mahdollinen arvo on $1$.
- Sinin pienin mahdollinen arvo on $-1$.
- Sini saa kaikki arvot väliltä $[-1,1]$.
Perustelu: Valitaan jokin arvo väliltä $[-1,1]$. Otetaan tätä arvoa vastaavalta korkeudelta yksikköympyrän kehäpiste. Tätä kehäpistettä vastaavan kulman sini on yhtä suuri kuin valittu arvo.
Sinin merkki
Päättele vastaukset seuraaviin kysymyksiin. Voit käyttää apuna alla näkyvää yksikköympyrää tai tätä Geogebra-havainnollistusta.
- Keksi jokin kulma, joka on välillä $\pa 90^\circ, 270^\circ \pe$ ja jonka sini on positiivinen.
- Keksi jokin kulma, joka on välillä $\pa 0^\circ, 360^\circ \pe$ ja jonka sini on negatiivinen.
- Missä koordinaatiston neljänneksessä kulman kehäpisteen pitää olla, jotta kulman sini on positiivinen?
Kertaa tarvittaessa koordinaatiston neljännesten numerointi kurssin MAA4 luvusta 1. - Missä koordinaatiston neljänneksessä kulman kehäpisteen pitää olla, jotta kulman sini on negatiivinen?

VASTAUS
Edellisten tehtävien tuloksista saadaan seuraava teoreema:
TEOREEMA
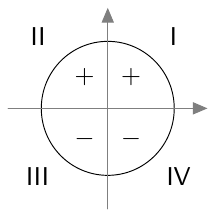
Kulman sinin arvo on aina lukujen $-1$ ja $1$ välissä: kaikilla kulmilla $\alpha$ pätee $$ -1 \leq \sin \alpha \leq 1. $$ Kulman sini on positiivinen, jos kulman kehäpiste on koordinaatiston I tai II neljänneksessä. Muussa tapauksessa kulman sini on negatiivinen.
Perustelu tehtävissä 1.4-1.5.
Sinin arvot ja merkki
Opiskelija löytää repustaan taulukkokirjasta irtirepeytyneen sivun, josta näkyy, että $$\sin 75^\circ = \frac{1}{4}\left(\sqrt{6} + \sqrt{2}\right).$$ Merkitse kulma $75^\circ$ yksikköympyrään ja päättele symmetrioiden avulla seuraavat sinin arvot:
- $\sin 105^\circ$
- $\sin (-75^\circ)$
- $\sin 255^\circ$
Vinkki: Aloita merkitsemällä jokainen kulma yksikköympyrään.
VASTAUS
- $\sin 105^\circ = \frac{1}{4}\left(\sqrt{6} + \sqrt{2}\right)$
- $\sin (-75^\circ) = -\frac{1}{4}\left(\sqrt{6} + \sqrt{2}\right)$
- $\sin 255^\circ = -\frac{1}{4}\left(\sqrt{6} + \sqrt{2}\right)$
Sinin ominaisuuksia
Tässä tehtävässä tutkitaan, miten sinin arvo muuttuu, jos suunnatun kulman kehäpiste ja loppukylki peilataan $y$- tai $x$-akselin suhteen. Peilaus $y$-akselin suhteen tehdään kuvittelemalla $y$-akseli peiliksi ja miettimällä, mihin kehäpisteen ja loppukyljen peilikuva muodostuu. Peilaus $x$-akselin suhteen tehdään vastaavasti, mutta peiliksi kuvitellaan $x$-akseli.
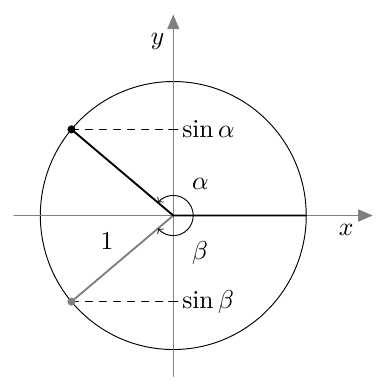
- Jos alla näkyvän suunnatun kulman $\beta$ kehäpiste ja loppukylki peilataan $y$-akselin suhteen, saadaan kulma $\gamma$. Mitä pystyt päättelemään luvuista $\sin \beta$ ja $\sin \gamma$? Selitä omin sanoin ja piirroksin.
- Jos alla näkyvän suunnatun kulman $\beta$ kehäpiste ja loppukylki peilataan $x$-akselin suhteen, saadaan kulma $\alpha$. Mitä pystyt päättelemään luvuista $\sin \beta$ ja $\sin \alpha$? Selitä omin sanoin ja piirroksin.
VASTAUS
- Sinin arvot ovat samat: $\sin \beta = \sin \gamma$.
- Sinin arvot ovat toistensa vastalukuja: $\sin \beta = -\sin \alpha$.
Tehtävän 1.7 johtopäätöksistä saadaan seuraava teoreema:
TEOREEMA
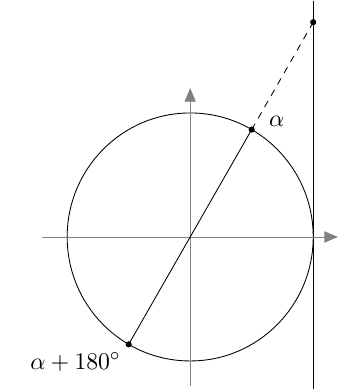
Kulmalla $\alpha$ ja sen suplementtikulmalla $180^\circ - \alpha$ on sama sini: $$ \sin(180^\circ - \alpha) = \sin \alpha $$ 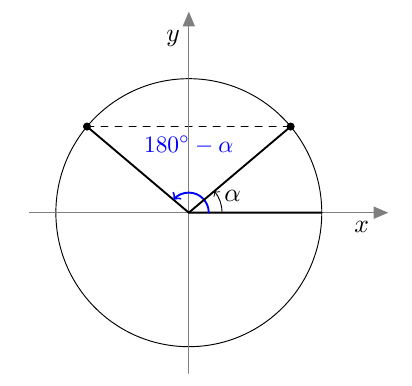
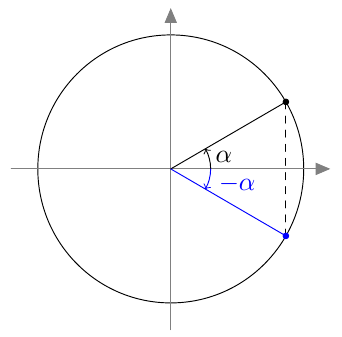
Kulman $\alpha$ ja sen vastakulman $-\alpha$ sinit ovat toistensa vastalukuja: $$ \sin(-\alpha) = -\sin \alpha $$ 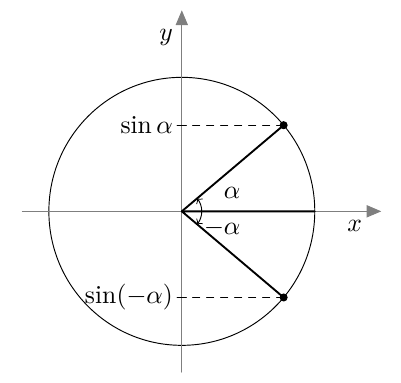
Perustelu tehtävässä 1.7.
Seuraavissa tehtävissä ryhdytään tutkimaan siniyhtälöiden ratkaisuja.
Siniyhtälö
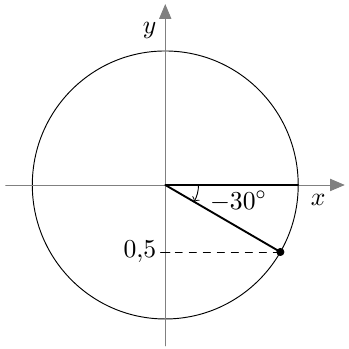
Tarkastellaan siniyhtälöä $$ \sin \alpha = -0{,}5. $$ Laskimen nappulan $\, \bbox[3px,border:2px solid black]{\texttt{sin}^{-1}}\ $ tai komennon $\, \texttt{arcsin}\, $ avulla löydetään yksi kulma, joka toteuttaa yhtälön. Tässä tapauksessa laskin antaa kulman $-30^\circ$. (Voit kokeilla, saatko omasta laskimestasi saman kulman.)
- Piirrä yksikköympyrä ja siihen laskimen antama kulma $-30^\circ$.
- Mitkä seuraavista kulmista toteuttavat tutkittavan yhtälön? Piirrä ne kaikki yksikköympyrään. Mitä yhteistä kulmilla on? Entä mitä eroa?
- $-30^\circ + 360^\circ$
- $-30^\circ + 2 \cdot 360^\circ$
- $-30^\circ + 5 \cdot 360^\circ$
- $-30^\circ + 100 \cdot 360^\circ$
- $-30^\circ + (-1) \cdot 360^\circ$
- $-30^\circ + (-7) \cdot 360^\circ$
- Miten voisit ilmaista kaikki edellä luetellut kulmat mahdollisimman lyhyesti kirjaimen $n$ avulla? Mitä kirjain $n$ tässä merkinnässä kuvaa?
- Päättele yksikköympyrän avulla jokin toinen kulma, joka toteuttaa yhtälön ja jolla on eri kehäpiste kuin edellä luetelluilla kulmilla.
- Ilmaise kirjaimen $n$ avulla kaikki kulmat, joilla on sama kehäpiste kuin d-kohdan kulmalla. Toteuttavatko ne yhtälön $\sin \alpha = -0{,}5$?
VASTAUS
-
- Kaikki luettelon kulmat toteuttavat yhtälön. Niillä on sama kehäpiste, mutta ne eroavat toisistaan jollain määrällä täysiä kierroksia (eli täyskulmia) positiiviseen tai negatiiviseen kiertosuuntaan.
- Kulmat ovat $-30^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku (kulmaan $-30^\circ$ lisättävien tai siitä vähennettävien täysien kierrosten määrä).
- Esimerkiksi $210^\circ$.
- Kulmat ovat $210^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku. Näillä kulmilla on sama kehäpiste kuin kulmalla $210^\circ$, joten ne kaikki toteuttavat yhtälön $\sin \alpha = -0{,}5$.
Siniyhtälö
Tarkastellaan siniyhtälöä $$ \sin \alpha = \frac{1}{\sqrt{2}}. $$
- Ratkaise laskimella yksi kulma, joka toteuttaa yhtälön. Löydät sen nappulan $\bbox[3px,border:2px solid black]{\texttt{sin}^{-1}}\ $ avulla.
- Piirrä yksikköympyrä ja siihen a-kohdassa löytämäsi kulma. Millä toisella kulmalla on sama sini mutta eri kehäpiste?
Vinkki: edellinen teoreema. - Mitä ovat ne kulmat, joilla on sama kehäpiste kuin a-kohdan kulmalla?
- Mitä ovat ne kulmat, joilla on sama kehäpiste kuin b-kohdan kulmalla?
- Milloin yhtälö $\,\sin \alpha = \dfrac{1}{\sqrt{2}}\,$ toteutuu?
VASTAUS
- Laskin antaa kulman $45^\circ$.
- Sama sini on suplementtikulmalla $180^\circ - 45^\circ = 135^\circ$.
- Kulmat saadaan a-kohdan kulmasta lisäämällä tai vähentämällä mikä tahansa määrä täysiä kierroksia eli täyskulmia: $45^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- Kulmat saadaan b-kohdan kulmasta lisäämällä tai vähentämällä mikä tahansa määrä täysiä kierroksia eli täyskulmia: $135^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- Yhtälö $$\sin \alpha = \dfrac{1}{\sqrt{2}}$$ toteutuu, jos ja vain jos \begin{align*} \alpha &= 45^\circ + n\cdot 360^\circ \text{ tai} \\ \alpha &= 135^\circ + n\cdot 360^\circ, \end{align*} missä $n$ on kokonaisluku.
Edellisen tehtävän päättelyä voidaan soveltaa minkä tahansa kulman tapauksessa, joten saadaan seuraava teoreema. Huomaa, että tiettyä kehäpistettä vastaa aina äärettömän monta kulmaa, jotka saadaan toisistaan lisäämällä tai vähentämällä täysiä kierroksia.
TEOREEMA
Oletetaan, että $\alpha_0$ on yksi kulma, joka toteuttaa yhtälön $\sin \alpha = a$. Yhtälön ratkaisu on tällöin \begin{align*} \alpha &= \alpha_0 + n \cdot 360^\circ \text{ tai} \\ \alpha &= 180^\circ - \alpha_0 + n \cdot 360^\circ, \end{align*} missä $n$ on kokonaisluku. 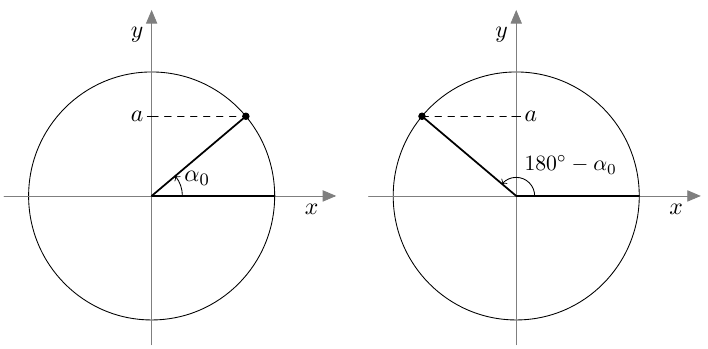
Perustelu samaan tapaan kuin tehtävässä 1.9.
Siniyhtälö
Ratkaise seuraavat yhtälöt ja havainnollista ratkaisuja yksikköympyrässä:
- $\sin \alpha = 0{,}5$
- $\sin \alpha = 1$
- $5\sin \alpha = -5$
- $3\sin \alpha = 0$
- $2\sin \alpha = -\sqrt{3}$
Vinkki kohtiin (c)-(e): selvitä ensin, mitä on $\sin \alpha$, ja ratkaise yhtälö tämän jälkeen normaalisti.
VASTAUS
- $\alpha = 30^\circ + n\cdot 360^\circ$ tai $\alpha = 150^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- $\alpha = 90^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- $\alpha = -90^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- $\alpha = n\cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha = -60^\circ + n\cdot 360^\circ$ tai $\alpha = 240^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
Seuraavissa tehtävissä tutkitaan erilaisia siniyhtälön muunnelmia.
Siniyhtälö
Tässä tehtävässä tutkitaan yhtälöitä $$2\sin \alpha = 1$$ ja $$\sin 2\alpha = 1.$$
- Mitä eroa yhtälöissä näyttää olevan? Selitä omin sanoin, mitä huomaat.
- Opiskelija ratkaisi yhtälön $2\sin \alpha = 1$. Tuloksen mukaan yhtälö toteutuu, jos ja vain jos $$ \alpha = 30^\circ + n \cdot 360^\circ $$ tai $$ \alpha = 150^\circ + n \cdot 360^\circ, $$ missä $n$ on kokonaisluku.
Havainnollista yksikköympyrässä kulmia $\alpha$. Miksi nämä kulmat $\alpha$ toteuttavat yhtälö $2\sin \alpha = 1$? - Opiskelija ratkaisi yhtälön $\sin 2\alpha = 1$. Tuloksen mukaan yhtälö toteutuu, jos ja vain jos $$ \alpha = 45^\circ + n \cdot 180^\circ, $$ missä $n$ on kokonaisluku. Havainnollista yksikköympyrässä kulmia $\alpha$ ja päättele vastaukset seuraaviin kysymyksiin:
- Mitä ovat ne kulmat, joiden sini on $1$?
- Miksi kulmat $\alpha$ toteuttavat yhtälön $\sin 2\alpha = 1$?
- Miksi ratkaisun kulmat $\alpha$ poikkeavat toisistaan vain oikokulman $180^\circ$ verran eivätkä kokonaista kierrosta?
VASTAUS
- Kulmat toteuttavat yhtälön $2\sin \alpha = 1$, sillä niille pätee $$ \sin \alpha = \frac{1}{2}. $$
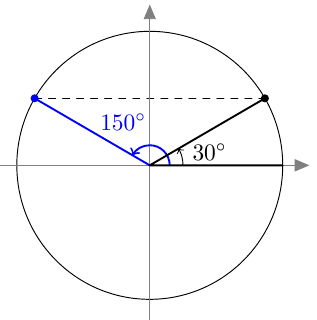
- Kulmat $\alpha$ yksikköympyrässä:
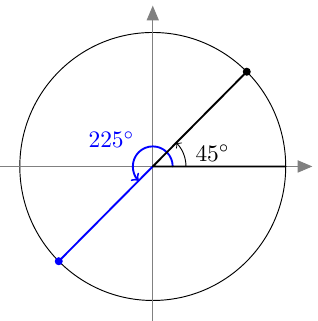
- Kulmat, joiden sini on $1$, ovat $90^\circ + n \cdot 360$, missä $n$ on kokonaisluku.
- Kulmat $\alpha = 45^\circ + n \cdot 180^\circ$ toteuttavat yhtälön $\sin 2\alpha = 1$, sillä $2\alpha = 90^\circ + n \cdot 360$.
- Kun yhtälöstä $$2\alpha = 90^\circ + n \cdot 360$$ ratkaistaan $\alpha$, pitää koko yhtälön oikea puoli jakaa luvulla 2.
Siniyhtälö
Tehtävänä on ratkaista yhtälö $$ \sin 3\alpha = \frac{1}{\sqrt{2}}. $$
- Selvitä laskimen avulla yksi kulma, jonka sinin arvo on $\frac{1}{\sqrt{2}}$.
- Päättele yksikköympyrän avulla kaikki kulmat, joiden sinin arvo on $\frac{1}{\sqrt{2}}$.
Vinkki: teoreema 3. - Muodosta b-kohdan avulla yhtälöt, jotka ilmaisevat kulman $3\alpha$ mahdolliset arvot.
- Ratkaise c-kohdan yhtälöistä kulma $\alpha$.
- Merkitse yksikköympyrään ne ratkaisut, jotka ovat välillä $[0^\circ, 360^\circ \pe$.
VASTAUS
- Laskin antaa kulman $45^\circ$.
- Sopivat kulmat ovat $45^\circ + n \cdot 360^\circ$ ja $135^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
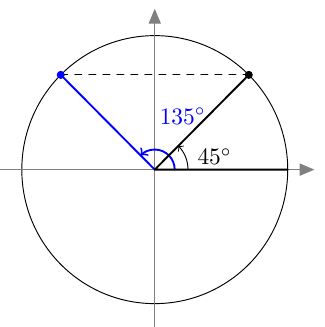
- Yhtälöt ovat $$ 3\alpha = 45^\circ + n \cdot 360^\circ $$ ja $$ 3\alpha = 135^\circ + n \cdot 360^\circ, $$ missä $n$ on kokonaisluku.
- Yhtälö $\sin 3\alpha = \frac{1}{\sqrt{2}}$ toteutuu, jos ja vain jos $$ \alpha = 15^\circ + n \cdot 120^\circ $$ tai $$ \alpha = 45^\circ + n \cdot 120^\circ, $$ missä $n$ on kokonaisluku.
- Ratkaisut yksikköympyrässä:
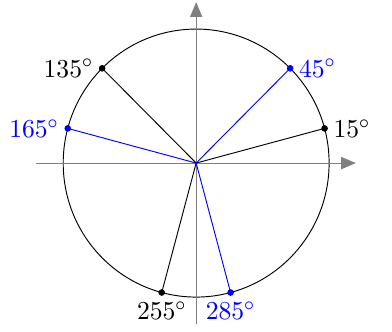
Kosini
Tässä kappaleessa yleistetään kulman kosinin käsite kaikille suunnatuille kulmille, tutkitaan kosinin ominaisuuksia ja opitaan ratkaisemaan erilaisia kosiniyhtälöitä yksikköympyrän avulla. Aloitetaan palauttamalla mieleen kulman kosinin aikaisempia määritelmiä.
Kurssilla MAA3 kulman kosini määriteltiin aluksi suorakulmaisen kolmion avulla: Suorakulmaisessa kolmiossa terävän kulman $\alpha$ kosini tarkoittaa kulman viereisen kateetin suhdetta hypoteenuusaan. Alla olevan kuvion merkinnöillä \begin{align*} \cos \alpha &= \textcolor{red}{\dfrac{\boldsymbol{b}}{\boldsymbol{c}}} \end{align*} 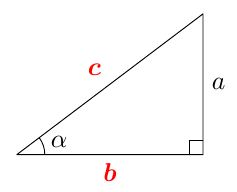 Tästä juontaa juurensa myös kosinin nimi. Kulman $\alpha$ kosini on nimittäin kolmion toisen terävän kulman, ns. komplementtikulman sini: \begin{align*} \cos \alpha &= \textcolor{red}{\dfrac{\boldsymbol{b}}{\boldsymbol{c}}} = \sin (90^\circ - \alpha). \end{align*} Kosini muistuttaa monilta ominaisuuksiltaan siniä. Kun opiskelet tätä kappaletta, pidä mielessä edellisen kappaleen asiat ja kokeile, pystytkö jo ennalta arvaamaan kosinin uuden määritelmän ja siitä seuraavat kosinin ominaisuudet.
Tästä juontaa juurensa myös kosinin nimi. Kulman $\alpha$ kosini on nimittäin kolmion toisen terävän kulman, ns. komplementtikulman sini: \begin{align*} \cos \alpha &= \textcolor{red}{\dfrac{\boldsymbol{b}}{\boldsymbol{c}}} = \sin (90^\circ - \alpha). \end{align*} Kosini muistuttaa monilta ominaisuuksiltaan siniä. Kun opiskelet tätä kappaletta, pidä mielessä edellisen kappaleen asiat ja kokeile, pystytkö jo ennalta arvaamaan kosinin uuden määritelmän ja siitä seuraavat kosinin ominaisuudet.
Jos $0^\circ \leq \alpha \leq 180^\circ$, määriteltiin kulman $\alpha$ kosini MAA3-kurssilla seuraavasti: Piirretään origosta lähtevä jana, jonka pituus on 1 ja joka muodostaa positiivisen $x$-akselin kanssa kulman $\alpha$. Kulman $\alpha$ kosini on tämän janan toisen päätepisteen $x$-koordinaatti:
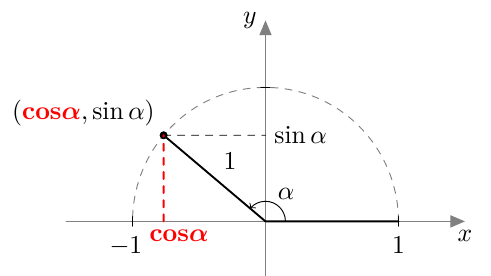
Kulman kosini
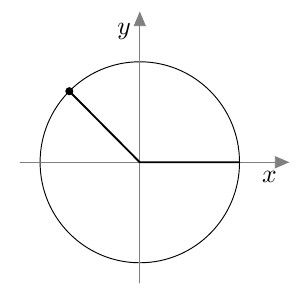
Tarkastele alla olevaa kuvaa.
- Määritä $\cos \beta$.
- Selvitä laskimella kulman $\beta$ suuruus. Anna vastaus kolmen merkitsevän numeron tarkkuudella. Kertaa tarvittaessa MAA3-kurssin tehtävä 1.20 ja sitä edeltävä teoriaosuus.
- Merkitse kulma $\beta$ koordinaatistoon. Onko välillä $[0^\circ, 180^\circ]$ jokin toinen kulma, jolla on sama kosini?
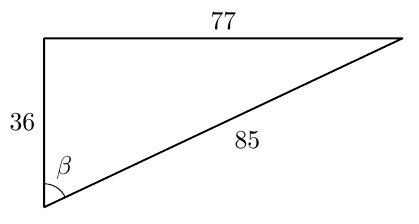
VASTAUS
- $\cos \beta = \dfrac{36}{85}$.
- $\beta \approx 64{,}9^\circ$
- Millään välin $[0^\circ, 180^\circ]$ kulmalla ei ole samaa kosinin arvoa.
Kosinin määritelmä voidaan laajentaa kaikille suunnattuille kulmille vastaavalla tavalla kuin sinin tapauksessa tehtiin:
MÄÄRITELMÄ: SUUNNATUN KULMAN KOSINI
Kulman $\alpha$ kosini on kulman $\alpha$ kehäpisteen $x$-koordinaatti:
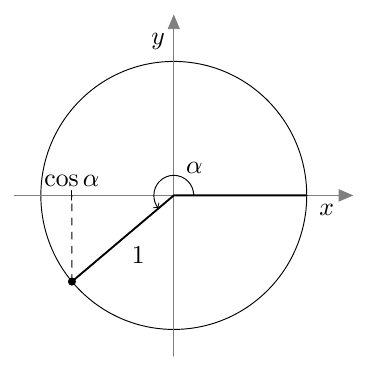
Suunnatun kulman kosini
Määritä tämän Geogebra-havainnollistuksen avulla seuraavat kosinin arvot kahden desimaalin tarkkuudella:
- $\cos 40^\circ$
- $\cos 105^\circ$
- $\cos 205^\circ$
- $\cos (-60^\circ )$
VASTAUS
- $\cos 40^\circ \approx 0{,}77$
- $\cos 105^\circ \approx -0{,}26$
- $\cos 205^\circ \approx -0{,}91$
- $\cos (-60^\circ ) = 0{,}5$
Seuraavissa tehtävissä tutkitaan kosinin ominaisuuksia yksikköympyrän avulla.
Kosinin arvot
Päättele vastaukset seuraaviin kysymyksiin. Voit käyttää apuna alla näkyvää yksikköympyrää tai tätä Geogebra-havainnollistusta.
- Mikä on suurin arvo, jonka kulman kosini voi saada?
- Mikä on pienin arvo, jonka kulman kosini voi saada?
- Onko kosinin suurimman ja pienimmän arvon välillä jonkin arvo, jota kosini ei koskaan saa? Selitä omin sanoin.

VASTAUS
- Kosinin suurin mahdollinen arvo on $1$.
- Kosinin pienin mahdollinen arvo on $-1$.
- Kosini saa kaikki arvot väliltä $[-1,1]$.
Perustelu: Valitaan jokin arvo väliltä $[-1,1]$. Otetaan tätä arvoa vastaavalta $x$-akselin kohdalta yksikköympyrän kehäpiste. Tätä kehäpistettä vastaavan kulman kosini on yhtä suuri kuin valittu arvo.
Kosinin merkki
Päättele vastaukset seuraaviin kysymyksiin. Voit käyttää apuna alla näkyvää yksikköympyrää tai tätä Geogebra-havainnollistusta.
- Keksi jokin kulma, joka on välillä $\pa 180^\circ, 360^\circ \pe$ ja jonka kosini on positiivinen.
- Keksi jokin kulma, joka on välillä $\pa 0^\circ, 180^\circ \pe$ ja jonka kosini on negatiivinen.
- Missä koordinaatiston neljänneksessä kulman kehäpisteen pitää olla, jotta kulman kosini on positiivinen?
Kertaa tarvittaessa koordinaatiston neljännesten numerointi kurssin MAA4 luvusta 1. - Missä koordinaatiston neljänneksessä kulman kehäpisteen pitää olla, jotta kulman kosini on negatiivinen?

VASTAUS
- Mikä tahansa kulma väliltä $\pa 270^\circ, 360^\circ]$.
- Mikä tahansa kulma väliltä $\pa 90^\circ, 180^\circ]$.
- I tai IV neljänneksessä, koska silloin kehäpisteen $x$-koordinaatti on positiivinen.
- II tai III neljänneksessä, koska silloin kehäpisteen $x$-koordinaatti on negatiivinen.
Edellisten tehtävien tuloksista saadaan seuraava teoreema:
TEOREEMA
Kulman kosinin arvo on aina lukujen $-1$ ja $1$ välissä: kaikilla kulmilla $\alpha$ pätee $$ -1 \leq \cos \alpha \leq 1. $$ Kulman kosini on positiivinen, jos kulman kehäpiste on koordinaatiston I tai IV neljänneksessä. Muussa tapauksessa kulman kosini on negatiivinen.
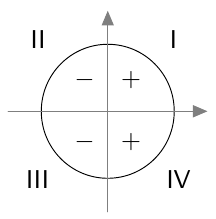
Perustelu tehtävissä 1.15-1.16.
Kosinin arvot ja merkki
Matematiikan professori löytää salkustaan taulukkokirjasta irtirepeytyneen sivun, josta näkyy, että $$\cos 108^\circ = -\frac{1}{4}\left(\sqrt{5} - 1\right).$$ Merkitse kulma $108^\circ$ yksikköympyrään ja päättele symmetrioiden avulla seuraavat kosinin arvot:
- $\cos 72^\circ$
- $\cos (-72^\circ)$
- $\cos 252^\circ$
Vinkki: Aloita merkitsemällä jokainen kulma yksikköympyrään.
VASTAUS
- $\cos 72^\circ = \frac{1}{4}\left(\sqrt{5} - 1\right)$
- $\cos (-72^\circ) = \frac{1}{4}\left(\sqrt{5} - 1\right)$
- $\cos 252^\circ = -\frac{1}{4}\left(\sqrt{5} - 1\right)$
Kosinin ominaisuuksia
Tässä tehtävässä tutkitaan, miten kosinin arvo muuttuu, jos suunnatun kulman kehäpiste ja loppukylki peilataan $x$- tai $y$-akselin suhteen. Peilaus $x$-akselin suhteen tehdään kuvittelemalla $x$-akseli peiliksi ja miettimällä, mihin kehäpisteen ja loppukyljen peilikuva muodostuu. Peilaus $y$-akselin suhteen tehdään vastaavasti, mutta peiliksi kuvitellaan $y$-akseli.
- Jos alla näkyvän suunnatun kulman $\beta$ kehäpiste ja loppukylki peilataan $x$-akselin suhteen, saadaan kulma $\alpha$. Mitä pystyt päättelemään luvuista $\cos \beta$ ja $\cos \alpha$? Selitä omin sanoin ja piirroksin.
- Jos alla näkyvän suunnatun kulman $\beta$ kehäpiste ja loppukylki peilataan $y$-akselin suhteen, saadaan kulma $\gamma$. Mitä pystyt päättelemään luvuista $\cos \beta$ ja $\cos \gamma$? Selitä omin sanoin ja piirroksin.
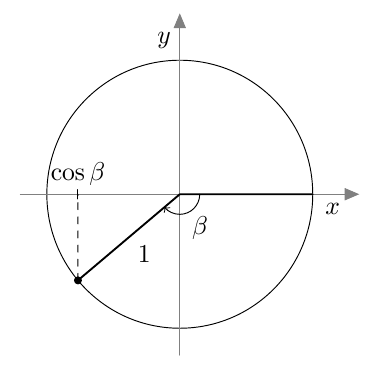
VASTAUS
- Kosinin arvot ovat samat: $\cos \beta = \cos \alpha$.
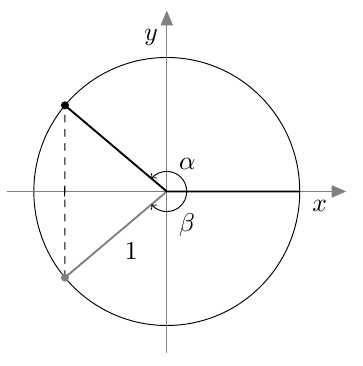
- Kosinin arvot ovat toistensa vastalukuja: $\cos \beta = -\cos \gamma$.
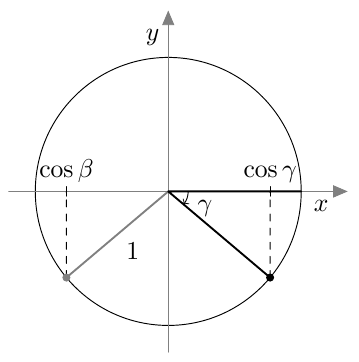
Tehtävän 1.18 johtopäätöksistä saadaan seuraava teoreema:
TEOREEMA
Kulmalla $\alpha$ ja sen vastakulmalla $-\alpha$ on sama kosini: $$ \cos(-\alpha) = \cos \alpha $$ 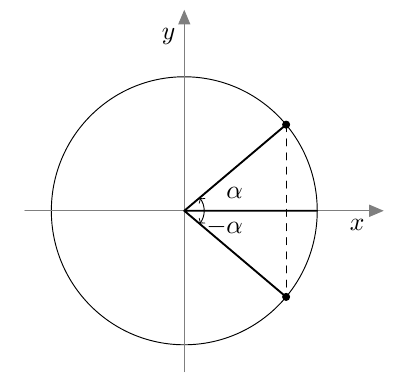
Kulman $\alpha$ ja sen suplementtikulman $180^\circ - \alpha$ kosinit ovat toistensa vastalukuja: $$ \cos(180^\circ - \alpha) = -\cos \alpha $$ 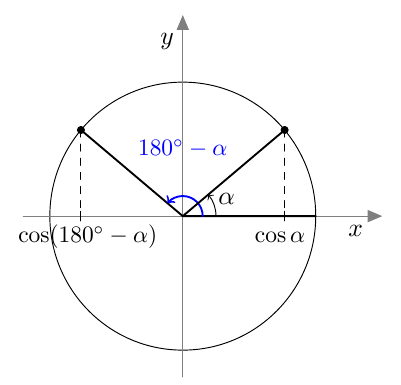
Perustelu tehtävässä 1.18.
Seuraavassa tehtävässä ryhdytään tutkimaan kosiniyhtälöiden ratkaisuja.
Kosiniyhtälö
Tarkastellaan kosiniyhtälöä $$ \cos \alpha = \frac{1}{2}. $$
- Ratkaise laskimella yksi kulma, joka toteuttaa yhtälön. Löydät sen nappulan $\bbox[3px,border:2px solid black]{\texttt{cos}^{-1}}\ $ avulla.
- Piirrä yksikköympyrä ja siihen a-kohdassa löytämäsi kulma. Millä toisella kulmalla on sama kosini?
Vinkki: edellinen teoreema. - Mitä ovat ne kulmat, joilla on sama kehäpiste kuin a-kohdan kulmalla?
- Mitä ovat ne kulmat, joilla on sama kehäpiste kuin b-kohdan kulmalla?
- Milloin yhtälö $\,\cos \alpha = \dfrac{1}{2}\,$ toteutuu?
VASTAUS
- Laskin antaa kulman $60^\circ$.
- Sama kosini on vastakulmalla $-60^\circ$.
- Kulmat saadaan a-kohdan kulmasta lisäämällä tai vähentämällä mikä tahansa määrä täysiä kierroksia eli täyskulmia: $60^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- Kulmat saadaan b-kohdan kulmasta lisäämällä tai vähentämällä mikä tahansa määrä täysiä kierroksia eli täyskulmia: $-60^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- Yhtälö $$\cos \alpha = \dfrac{1}{2}$$ toteutuu, jos ja vain jos \begin{align*} \alpha &= \phantom{-}60^\circ + n\cdot 360^\circ \text{ tai} \\ \alpha &= -60^\circ + n\cdot 360^\circ, \end{align*} missä $n$ on kokonaisluku.
Edellisen tehtävän päättelyä voidaan soveltaa minkä tahansa kulman tapauksessa, joten saadaan seuraava teoreema:
TEOREEMA
Oletetaan, että $\alpha_0$ on yksi kulma, joka toteuttaa yhtälön $\cos \alpha = a$. Yhtälön ratkaisu on tällöin \begin{align*} \alpha &= \phantom{-}\alpha_0 + n \cdot 360^\circ \text{ tai} \\ \alpha &= -\alpha_0 + n \cdot 360^\circ, \end{align*} missä $n$ on kokonaisluku. 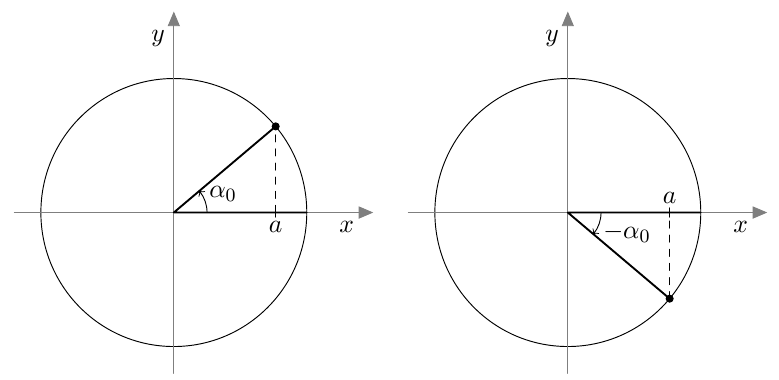
Perustelu samaan tapaan kuin tehtävässä 1.19.
Seuraavissa tehtävissä harjoitellaan kosiniyhtälöiden ratkaisemista. Vastaavia siniyhtälöitä ratkotiin jo aikaisemmin tehtävissä 1.10-1.12.
Kosiniyhtälö
Ratkaise seuraavat yhtälöt ja havainnollista ratkaisuja yksikköympyrässä:
- $\cos \alpha = 0$
- $\cos \alpha = -1$
- $2\cos \alpha = \sqrt{3}$
- $-\frac{1}{4}\cos \alpha = -\frac{1}{4}$
- $\sqrt{2}\cos \alpha = -1$
VASTAUS
- $\alpha = 90^\circ + n\cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha = 180^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- $\alpha = 30^\circ + n\cdot 360^\circ$ tai $\alpha = -30^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- $\alpha = n\cdot 360^\circ$, missä $n$ on kokonaisluku.
- $\alpha = 135^\circ + n\cdot 360^\circ$ tai $\alpha = -135^\circ + n\cdot 360^\circ$, missä $n$ on kokonaisluku.
Kosiniyhtälö
Tehtävänä on ratkaista yhtälö $$ \cos 4\alpha = \frac{\sqrt{3}}{2}. $$
- Selvitä laskimen avulla yksi kulma, jonka kosinin arvo on $\frac{\sqrt{3}}{2}$.
- Päättele yksikköympyrän avulla kaikki kulmat, joiden kosinin arvo on $\frac{\sqrt{3}}{2}$.
Vinkki: teoreema 6. - Muodosta b-kohdan avulla yhtälöt, jotka ilmaisevat kulman $4\alpha$ mahdolliset arvot.
- Ratkaise c-kohdan yhtälöistä kulma $\alpha$.
- Merkitse yksikköympyrään ne ratkaisut, jotka ovat välillä $[0^\circ, 360^\circ \pe$.
VASTAUS
- Laskin antaa kulman $30^\circ$.
- Sopivat kulmat ovat $30^\circ + n \cdot 360^\circ$ ja $-30^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
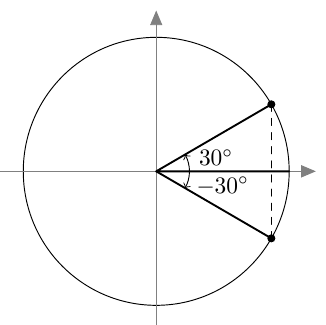
- Yhtälöt ovat $$ 4\alpha = 30^\circ + n \cdot 360^\circ $$ ja $$ 4\alpha = -30^\circ + n \cdot 360^\circ, $$ missä $n$ on kokonaisluku.
- Yhtälö $\cos 4\alpha = \frac{\sqrt{3}}{2}$ toteutuu, jos ja vain jos $$ \alpha = 7{,}5^\circ + n \cdot 90^\circ $$ tai $$ \alpha = -7{,}5^\circ + n \cdot 90^\circ, $$ missä $n$ on kokonaisluku.
- Ratkaisut yksikköympyrässä:
Tutkitaan seuraavaksi, miten kulman sini ja kosini liittyvät toisiinsa. Tässä auttaa Pythagoraan lause (MAA3-kurssin teoreema 4).
Sinin ja kosinin yhteys
Tässä tehtävässä johdetaan yhtälö, joka yhdistää toisiinsa kulman sinin ja kosinin arvot.
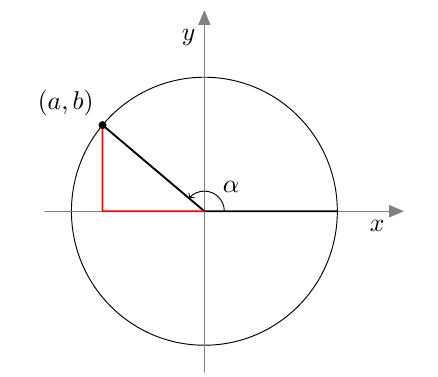
- Piirrä yksikköympyrä ja siihen jonkin kulma $\alpha$, jonka kehäpiste ei ole koordinaattiakseleilla. Voit katsoa mallia alla olevasta kuvasta.
- Täydennä kuvaan suorakulmainen kolmio, jonka
- kateetit ovat koordinaattiakselien suuntaiset
- hypotenuusa yhdistää origon ja kulman $\alpha$ kehäpisteen $(a,b)$.
- Miten b-kohdan kolmion sivujen pituudet liittyvät toisiinsa Pythagoraan lauseen mukaan?
- Lausu kulman $\alpha$ kehäpisteen koordinaatit kosinin ja sinin avulla. Sijoita ne c-kohdan yhtälöön.
- Toteutuuko d-kohdan yhtälö, jos kulman $\alpha$ kehäpiste on koordinaattiakselilla? Tarkista kaikki neljä mahdollista tapausta.
VASTAUS
- Esimerkiksi alla olevassa kuvassa kateettien pituudet ovat $\left|a\right|$ ja $b$. Hypotenuusan pituus on 1, koska kysymyksessä on yksikköympyrä.
- Pythagoraan lauseen mukaan $a^2 + b^2 = 1$. Huomaa, ettei itseisarvomerkkejä tarvita toiseen potenssiin korotuksen vuoksi.
- Kehäpiste on $(a,b) = (\cos \alpha, \sin \alpha)$. Yhtälö on $$ (\cos \alpha)^2 + (\sin \alpha)^2 = 1. $$
- Jos kehäpiste on koordinaattiakselilla, se on $(1,0)$, $(-1,0)$, $(0,1)$ tai $(0,-1)$. Havaitaan, että d-kohdan yhtälö toteutuu myös näissä tapauksissa.
Sinin ja kosinin potenssit merkitään yleensä kirjoittamalla eksponentti jo ennen kulmaa: $\sin^2\!\alpha$ ja $\cos^2\!\alpha$. Nämä ovat siis lyhennysmerkintöjä, joiden avulla voidaan yhdet sulut jättää pois: \begin{align*} \sin^2\! \alpha &= (\sin \alpha)^2 \\ \cos^2\! \alpha &= (\cos \alpha)^2 \end{align*} Muotoillaan tehtävän 1.22 tuloksena syntyvä teoreema näitä merkintöjä käyttäen:
TEOREEMA
Jokaisen kulman sinin ja kosinin neliöiden summa on 1: $$ \sin^2\! \alpha + \cos^2 \! \alpha = 1. $$ 
Perustelu tehtävässä 1.22.
Teoreeman 7 tulosta voidaan hyödyntää muun muassa sinin ja kosinin tarkkojen arvojen määrittämisessä sekä joidenkin yhtälöiden ratkaisussa. Tätä harjoitellaan seuraavissa tehtävissä.
Sinin ja kosinin yhteys
Tehtävänä on määritää kulman $\alpha$ sinin tarkka arvo, kun tiedetään, että $$ \cos \alpha = \frac{35}{37} $$ ja että $180^\circ \leq \alpha \leq 360^\circ$.
- Selvitä edellisen teoreeman avulla, mikä on lausekkeen $\sin^2\! \alpha$ tarkka arvo.
- Mitä voit päätellä kulman $\alpha$ sinin merkistä tiedon $180^\circ \leq \alpha \leq 360^\circ$ perusteella?
- Päättele a- ja b-kohtien perusteella, mikä on kulman $\alpha$ sinin tarkka arvo.
VASTAUS
- $\sin^2\! \alpha = \dfrac{144}{1369}$
- Sinin arvo on negatiivinen (tai nolla).
- $\sin \alpha = -\sqrt{\dfrac{144}{1369}} = -\dfrac{12}{37}$
Sinin ja kosinin yhteys
Tehtävänä on ratkaista yhtälö $$ 2\sin^2\! \alpha + \cos \alpha = \frac{3}{2}. $$
- Muokkaa yhtälöä teoreeman 7 avulla niin, että siinä esiintyy vain kosinin potensseja. Toisin sanottuna korvaa $\sin^2\! \alpha$ sopivalla lausekkeella.
- Muokkaa yhtälö muotoon $$ a\cos^2\! \alpha + b\cos \alpha + c = 0. $$
- Ratkaise $\cos \alpha$ toisen asteen yhtälön ratkaisukaavalla (MAA2-kurssin teoreema 5).
- Kohdan (c) tuloksena saat kaksi yhtälöä kulman $\alpha$ kosinille. Ratkaise nämä yhtälöt normaaliin tapaan.
Vinkki: katso tarvittaessa mallia tehtävästä 1.19.
VASTAUS
- Teoreeman 7 mukaan $\sin^2\! \alpha = 1 - \cos^2\! \alpha$. Tällä sijoituksella yhtälö saadaan muotoon $$ 2 - 2\cos^2\! \alpha + \cos \alpha = \frac{3}{2} $$
- $$ - 2\cos^2\! \alpha + \cos \alpha + \frac{1}{2} = 0 $$
- $$ \cos \alpha = \frac{-1 \pm \sqrt{5}}{-4} $$
- Yhtälö $\cos \alpha = \frac{-1 + \sqrt{5}}{-4}$ toteutuu, jos ja vain jos $\alpha = 108^\circ + n \cdot 360^\circ$ tai $\alpha = -108^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
Yhtälö $\cos \alpha = \frac{-1 - \sqrt{5}}{-4}$ toteutuu, jos ja vain jos $\alpha = 36^\circ + n \cdot 360^\circ$ tai $\alpha = -36^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
Tangentti
Tässä kappaleessa laajennetaan kulman tangentin määritelmä suunnatuille kulmille yksikköympyrän avulla, tutkitaan tangentin ominaisuuksia ja opitaan ratkaisemaan erilaisia tangenttiyhtälöitä.
Kurssilla MAA3 kulman tangentti määriteltiin suorakulmaisen kolmion avulla: Suorakulmaisessa kolmiossa terävän kulman $\alpha$ tangentti tarkoittaa kulman vastaisen kateetin suhdetta viereiseen kateettiin. Alla olevan kuvion merkinnöillä \begin{align*} \tan \alpha &= \textcolor{red}{\dfrac{\boldsymbol{a}}{\boldsymbol{b}}} \end{align*} 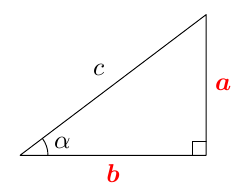
Kulman tangentti
Tarkastele alla olevaa kuvaa.
- Määritä $\tan \gamma$.
- Selvitä laskimella kulman $\gamma$ suuruus. Anna vastaus kolmen merkitsevän numeron tarkkuudella. Kertaa tarvittaessa MAA3-kurssin tehtävä 1.20 ja sitä edeltävä teoriaosuus.
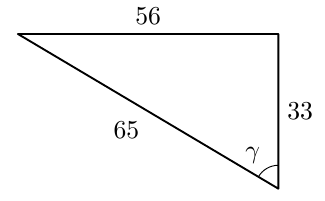
VASTAUS
- $\tan \gamma = \dfrac{56}{33}$.
- $\gamma \approx 59{,}5^\circ$
Sini ja kosini määriteltiin aikaisemmin kaikille suunnatuille kulmille kulman kehäpisteen avulla. Tangentin määrittelemiseksi tarvitaan samantyyppinen uusi käsite, kulman tangenttipiste:
MÄÄRITELMÄ: KULMAN TANGENTTIPISTE
Piirretään yksikköympyrälle $y$-askelin suuntainen tangentti pisteeseen $(1,0)$. Tämän tangenttisuoran ja suunnatun kulman $\alpha$ loppukyljen tai sen jatkeen leikkauspiste $B$ on kulman $\alpha$ tangenttipiste:
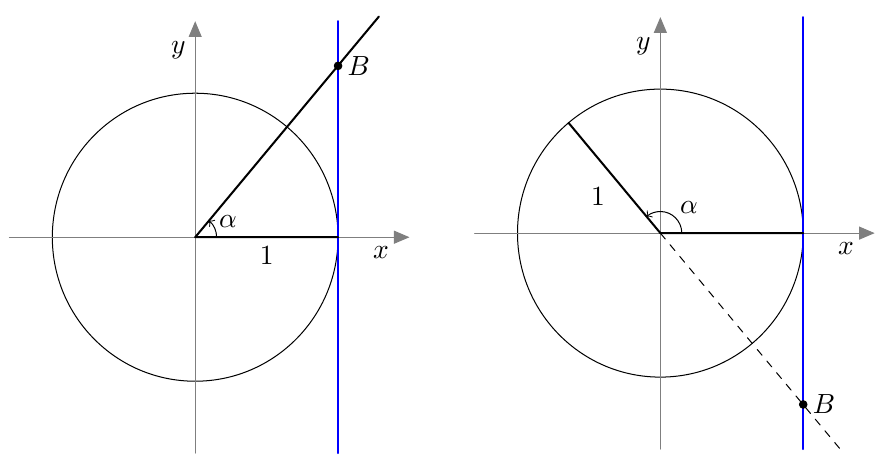
Kulman tangenttipiste
Lähes kaikkien suunnattujen kulmien loppukylki tai sen jatke leikkaa jossain vaiheessa yksikköympyrälle pisteeseen $(1,0)$ asetetun tangentin. On kuitenkin olemassa kulmia, joiden loppukylki ei koskaan leikkaa tätä tangenttisuoraa. Mitä nämä kulmat ovat?
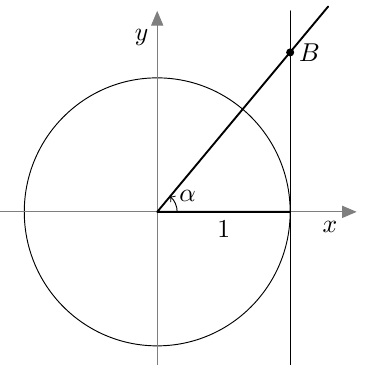
Voit käyttää päättelyssä yllä olevaa kuvaa. Keksitkö ainakin neljä kulmaa, joista kahdella on eri kehäpiste?
VASTAUS
Jos kulman loppukylki on $y$-akselilla, ei se eikä sen jatke leikkaa yksikköympyrälle pisteeseen $(1,0)$ asetettua tangentia. Nämä kulmat ovat $90^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
Tangenttipisteen käsitteen avulla voimme nyt laajentaa tangentin määritelmän lähes kaikille suunnattuille kulmille:
MÄÄRITELMÄ: SUUNNATUN KULMAN TANGENTTI
Oletetaan, että kulman $\alpha$ kehäpiste ei ole $y$-akselilla eli $\alpha \neq 90^\circ + n \cdot 180^\circ$ kaikilla kokonaisluvuilla $n$.
Kulman $\alpha$ tangentti on kulman $\alpha$ tangenttipisteen $y$-koordinaatti:
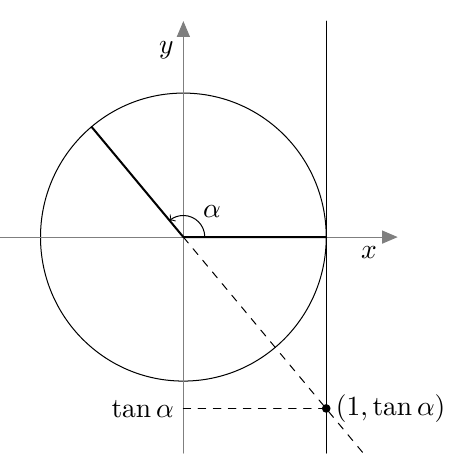
Suunnatun kulman tangentti
Määritä tämän Geogebra-havainnollistuksen avulla seuraavat tangentin arvot kahden desimaalin tarkkuudella:
- $\tan 40^\circ$
- $\tan 145^\circ$
- $\tan 205^\circ$
- $\tan (-75^\circ )$
VASTAUS
- $\tan 40^\circ \approx 0{,}84$
- $\tan 145^\circ \approx -0{,}70$
- $\tan 205^\circ \approx 0{,}47$
- $\tan (-75^\circ ) \approx -3{,}73$
Seuraavassa tehtävässä tutkitaan tangentin ominaisuuksia yksikköympyrän avulla.
Tangentin arvot ja merkki
Päättele vastaukset seuraaviin kysymyksiin. Voit käyttää apuna alla näkyvää yksikköympyrää tai tätä Geogebra-havainnollistusta.
- Keksi jotkin kulmat $\alpha$ ja $\beta$, jotka ovat välillä $\pa 180^\circ, 360^\circ \pe$ ja joille pätee $\tan \alpha > 0$ ja $\tan \beta < 0$.
- Missä koordinaatiston neljänneksessä kulman kehäpisteen pitää olla, jotta kulman tangentti on positiivinen? Entä negatiivinen?
- Mitä arvoja kulman tangentti voi saada?

VASTAUS
- Mitkä tahansa $\alpha \in \pa 180^\circ, 270^\circ\pe$ ja $\beta \in \pa 270^\circ, 360^\circ\pe$.
- Tangentti on positiivinen, jos ja vain jos kulman kehäpiste on I tai III neljänneksessä. Tangentti on negatiivinen, jos ja vain jos kulman kehäpiste on II tai IV neljänneksessä.
- Kulman tangentti saa kaikki reaalilukuarvot, kun kulma käy läpi esimerkiksi välin $\pa -90^\circ, 90^\circ \pe$.
Perustelu: Valitaan jokin reaaliluku $t$. Piirretään jana, joka yhdistää pisteen $(1,t)$ origoon. Tämä jana on jonkin kulman $-90^\circ < \alpha < 90^\circ$ loppukylki ja piste $(1,t)$ on kulman $\alpha$ tangenttipiste. Siten $\tan \alpha = t$.
Edellisen tehtävän tuloksista saadaan seuraava teoreema:
TEOREEMA
Kulman tangentti voi olla mikä tahansa reaaliluku. Kulman tangentti on positiivinen, jos kulman kehäpiste on koordinaatiston I tai III neljänneksessä. Muussa tapauksessa kulman tangentti on negatiivinen.
Perustelu tehtävässä 1.28.
Tangentin arvot ja merkki
Siivooja löytää käytävältä taulukkokirjasta irtirepeytyneen sivun, josta näkyy, että $$\tan 195^\circ = 2 - \sqrt{3}.$$ Merkitse kulma $195^\circ$ yksikköympyrään ja päättele symmetrioiden avulla seuraavat tangentin arvot:
- $\tan 15^\circ$
- $\tan 165^\circ$
- $\tan 345^\circ$
Vinkki: Aloita merkitsemällä jokainen kulma yksikköympyrään.
VASTAUS
- $\tan 15^\circ = 2 - \sqrt{3}$
- $\tan 165^\circ = \sqrt{3} - 2$
- $\tan 345^\circ = \sqrt{3} - 2$
Tangentin ominaisuuksia
Tässä tehtävässä tutkitaan, miten tangentin arvo muuttuu, jos suunnatun kulman kehäpiste ja loppukylki peilataan $x$- tai $y$-akselin suhteen.
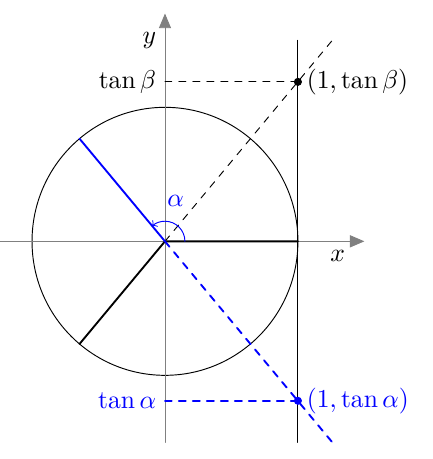
- Jos alla näkyvän suunnatun kulman $\beta$ kehäpiste ja loppukylki peilataan $x$-akselin suhteen, saadaan kulma $\alpha$. Mitä pystyt päättelemään luvuista $\tan \beta$ ja $\tan \alpha$? Selitä omin sanoin ja piirroksin.
- Jos alla näkyvän suunnatun kulman $\beta$ kehäpiste ja loppukylki peilataan $y$-akselin suhteen, saadaan kulma $\gamma$. Mitä pystyt päättelemään luvuista $\tan \beta$ ja $\tan \gamma$? Selitä omin sanoin ja piirroksin.
VASTAUS
- Tangentin arvot ovat toistensa vastalukuja: $\tan \alpha = -\tan \beta$.
- Tangentin arvot ovat toistensa vastalukuja: $\tan \gamma = -\tan \beta$.
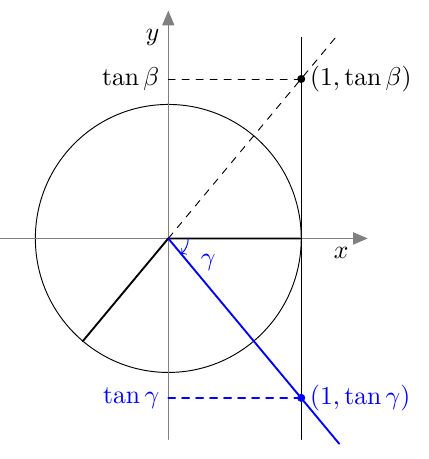
Tehtävän 1.30 johtopäätöksistä saadaan seuraava teoreema:
TEOREEMA
Kulman $\alpha$ ja sen vastakulman $-\alpha$ tangentit ovat toistensa vastalukuja: $$ \tan(-\alpha) = -\tan \alpha $$ 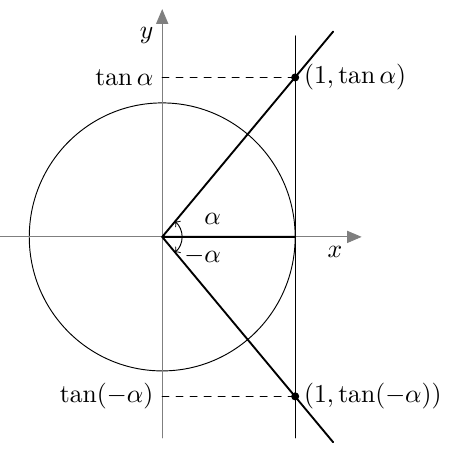
Kulman $\alpha$ ja sen suplementtikulman $180^\circ - \alpha$ tangentit ovat toistensa vastalukuja: $$ \tan(180^\circ - \alpha) = -\tan \alpha $$ 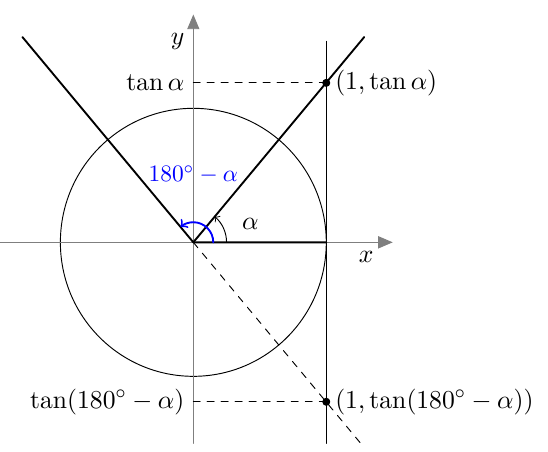
Perustelu tehtävässä 1.30.
Seuraavassa tehtävässä tutkitaan tangenttiyhtälöiden ratkaisuja.
Tangenttiyhtälö
Tarkastellaan tangenttiyhtälöä $$ \tan \alpha = -\sqrt{3}. $$
- Ratkaise laskimella yksi kulma, joka toteuttaa yhtälön. Löydät sen nappulan $\bbox[3px,border:2px solid black]{\texttt{tan}^{-1}}\ $ avulla.
- Piirrä yksikköympyrä ja siihen a-kohdassa löytämäsi kulma. Päättele yksikköympyrän avulla, millä kulmalla on sama tangentti mutta eri kehäpiste.
- Milloin yhtälö $\,\tan \alpha = -\sqrt{3}\,$ toteutuu?
VASTAUS
- Laskin antaa kulman $-60^\circ$.
- Sama tangentti mutta eri kehäpiste on kulmalla $-60^\circ + 180^\circ = 120^\circ$.
- Yhtälö $$\tan \alpha = -\sqrt{3}$$ toteutuu, jos ja vain jos $\alpha = 120^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
Edellisen tehtävän päättelyä voidaan soveltaa minkä tahansa kulman tapauksessa, joten saadaan seuraava teoreema:
TEOREEMA
Oletetaan, että $\alpha_0$ on yksi kulma, joka toteuttaa yhtälön $\tan \alpha = a$. Yhtälön ratkaisu on tällöin \begin{align*} \alpha &= \alpha_0 + n \cdot 180^\circ, \end{align*} missä $n$ on kokonaisluku. 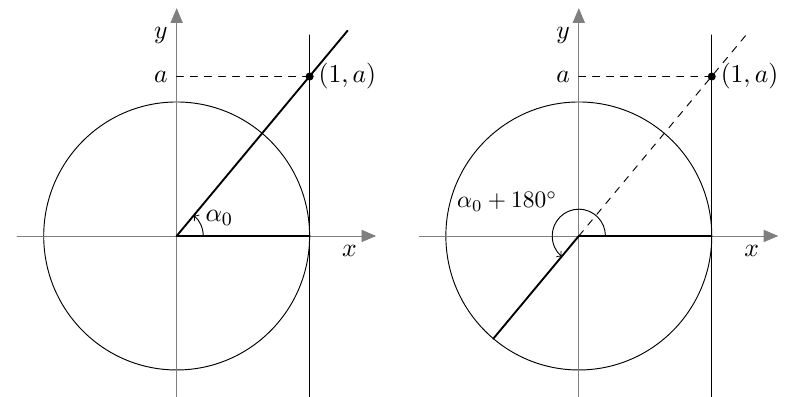
Perustelu samaan tapaan kuin tehtävässä 1.31.
Tangenttiyhtälö
Ratkaise seuraavat yhtälöt ja havainnollista ratkaisuja yksikköympyrässä:
- $\tan \alpha = 1$
- $-2\tan \alpha = 0$
- $\sqrt{3}\tan \alpha = -1$
- $\sqrt{2} + \tan \alpha = 1$
VASTAUS
- $\alpha = 45^\circ + n\cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha = n\cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha = -30^\circ + n\cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha = -22{,}5^\circ + n\cdot 180^\circ$, missä $n$ on kokonaisluku.
Tangenttiyhtälö
Tehtävänä on ratkaista yhtälö $$ \tan 6\alpha = 2 + \sqrt{3}. $$
- Selvitä laskimen avulla yksi kulma, jonka tangentin arvo on $2 + \sqrt{3}$.
- Päättele yksikköympyrän avulla kaikki kulmat, joiden tangentin arvo on $2 + \sqrt{3}$.
Vinkki: teoreema 10. - Muodosta b-kohdan avulla yhtälö, joka ilmaisee kulman $6\alpha$ mahdolliset arvot.
- Ratkaise c-kohdan yhtälöstä kulma $\alpha$.
- Merkitse yksikköympyrään ne ratkaisut, jotka ovat välillä $[0^\circ, 360^\circ \pe$.
VASTAUS
- Laskin antaa kulman $75^\circ$.
- Sopivat kulmat ovat $75^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
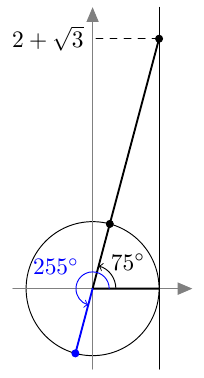
- Yhtälö on $$ 6\alpha = 75^\circ + n \cdot 180^\circ, $$ missä $n$ on kokonaisluku.
- Yhtälö $\tan 6\alpha = 2 + \sqrt{3}$ toteutuu, jos ja vain jos $$ \alpha = 12{,}5^\circ + n \cdot 30^\circ, $$ missä $n$ on kokonaisluku.
- Ratkaisut yksikköympyrässä:
Tutkitaan seuraavaksi, miten tangentti liittyy siniin ja kosiniin.
Tangentin yhteys siniin ja kosiniin
Tässä tehtävässä johdetaan yhtälö, joka yhdistää toisiinsa kulman tangentin, sinin ja kosinin arvot.
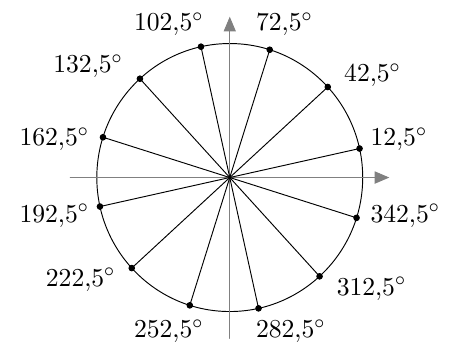
- Alla on näkyvissä yksikköympyrä ja siinä kaksi suorakulmaista kolmiota: $OCA$ ja $ODB$. Mikä on janan $OD$ pituus? Ilmaise janojen $OC$, $AC$ ja $BD$ pituudet kulman $\alpha$ avulla.
- Mitä voit päätellä suhteista $\dfrac{BD}{OD}$ ja $\dfrac{AC}{OC}$?
- Millaisen yhtälön saat a- ja b-kohtien avulla kulman $\alpha$ tangentin, sinin ja kosinin välille?
VASTAUS
- $OD = 1$, $OC = \cos \alpha$, $AC = \sin \alpha$ ja $BD = \tan \alpha$.
- Kolmioissa $OCA$ ja $ODB$ on kaksi yhtä suurta kulmaa (kulma $\alpha$ ja suora kulma), joten ne ovat yhdenmuotoiset (MAA3-kurssin teoreema 3). Tästä seuraa, että $$ \dfrac{BD}{OD} = \dfrac{AC}{OC} $$
- Yhtälö on $$ \dfrac{\tan \alpha}{1} = \dfrac{\sin \alpha}{\cos \alpha} $$ eli $$ \tan \alpha = \dfrac{\sin \alpha}{\cos \alpha} $$
Tehtävän 1.34 tulos saadaan laajennettua seuraavaksi yleispäteväksi teoreemaksi:
TEOREEMA
Kulman $\alpha$ tangentti on sinin ja kosinin osamäärä: $$ \tan \alpha = \frac{\sin\alpha}{\cos \alpha}. $$
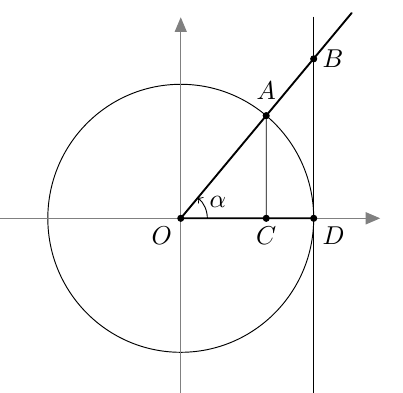
Perustelu: Tapaus, jossa kulman $\alpha$ kehäpiste on koordinaatiston I neljänneksessä, on käsitelty tehtävässä 1.34. Tapausta, jossa kehäpiste on II neljänneksessä, on havainnollistettu kuvassa alla.
Kolmioissa $OCA$ ja $ODB$ on kaksi yhtä suurta kulmaa (suorat kulmat sekä kuvaan merkityt ristikulmat), joten ne ovat yhdenmuotoiset. Tästä seuraa, että $$ \dfrac{BD}{OD} = \dfrac{AC}{OC}. $$ Kun tähän yhtälöön sijoitetaan janojen pituudet $BD = -\tan \alpha$, $OD = 1$, $AC = \sin \alpha$ ja $OC = -\cos \alpha$, päädytään sievennyksen jälkeen yhtälöön $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha}. $$ Huomaa, että tässä tapauksessa kulman $\alpha$ tangentti ja kosini ovat negatiivisia, joten vastaavat janojen pituudet ovat niiden vastalukuja: $BD = -\tan \alpha$ ja $OC = -\cos \alpha$. Miinusmerkit kuitenkin katoavat sievennyksessä.
Tapaukset, joissa kulman kehäpiste on koordinaatiston III tai IV neljänneksessä, voidaan käsitellä vastaavalla tavalla.
Teoreeman 11 avulla voidaan määrittää tangentin tarkkoja arvoja ja ratkaista joitakin trigonometrisia yhtälöitä kuten seuraavissa tehtävissä tehdään.
Tangentin yhteys siniin ja kosiniin
Määritä $\tan \alpha$, kun tiedetään, että $$ \sin \alpha = \dfrac{12}{37} $$ ja että $$ \cos \alpha = -\frac{35}{37}. $$ Missä neljänneksessä kulman $\alpha$ kehäpiste sijaitsee?
VASTAUS
Sinin ja kosinin merkeistä voidaan päätellä, että kulman $\alpha$ kehäpiste sijaitsee II neljänneksessä. Tangentin arvo on $$ \tan \alpha = -\dfrac{12}{35} $$
Tangentin yhteys siniin ja kosiniin
Tehtävänä on ratkaista asteen kymmenesosan tarkkuudella yhtälö $$ 4\sin \alpha - 9 \cos \alpha = 0. $$
- Toteutuuko yhtälö, jos $\cos \alpha = 0$?
Vinkki: Mieti yksikköympyrän avulla, mitä on $\sin \alpha$, jos $\cos \alpha = 0$. - Muokkaa yhtälöä niin, että saat selville suhteen $$ \frac{\sin\alpha}{\cos \alpha}. $$ Miksi voit olettaa, että jakaja $\cos \alpha \neq 0$?
Vinkki: a-kohta. - Muodosta vastaava tangenttiyhtälö teoreeman 11 avulla ja ratkaise se.
Vinkki: teoreema 10.
VASTAUS
- Yhtälö ei toteudu, jos $\cos \alpha = 0$. Nimittäin tässä tapauksessa $\sin \alpha = \pm 1$ ja $$ 4\sin \alpha - 9 \cos \alpha = \pm 4 \neq 0. $$
- Koska yhtälö ei toteudu, kun $\cos \alpha = 0$, voidaan olettaa, että $\cos \alpha \neq 0$. Tällöin yhtälöstä saadaan ratkaistua $$ \frac{\sin\alpha}{\cos \alpha} = \frac{9}{4}. $$
- Yhtälön $$ \tan \alpha = \frac{9}{4} $$ ratkaisuiksi saadaan laskimen ja yksikköympyrän avulla $$ \alpha \approx 66{,}0^\circ + n \cdot 180^\circ, $$ missä $n$ on kokonaisluku.
TEHTÄVÄSARJA II
Sini ja kosini
Laske lausekkeen $4\sin 3\alpha - \cos 2\alpha$ arvo, kun
- $\alpha = 90^\circ$
- $\alpha = 180^\circ$
Päättele sinin ja kosinin arvot yksikköympyrän avulla. Voit tarkistaa tulokset laskimella.
Vastaus
- $4\sin 270^\circ - \cos 180^\circ = -3$
- $4\sin 540^\circ - \cos 360^\circ = -1$
Sini
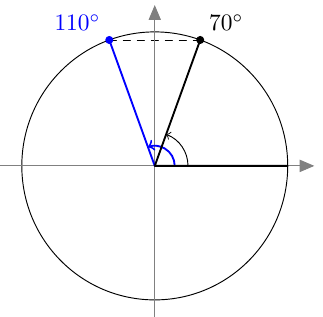
Merkitse kulma $\beta$ yksikköympyrään ja päättele, millä välin $[0^\circ, 360^\circ \pe$ kulmilla on sama sinin arvo kuin kulmalla $\beta$.
- $\beta = 790^\circ$
- $\beta = 560^\circ$
Vinkki: tutki ensin, kuinka monta täyttä kierrosta kulmaan $\beta$ sisältyy.
Vastaus
- Sama sinin arvo on kulmilla $70^\circ$ ja $110^\circ$.
Huom. kulma $70^\circ$ löydetään vähentämällä annetusta kulmasta kaksi täyttä kierrosta.
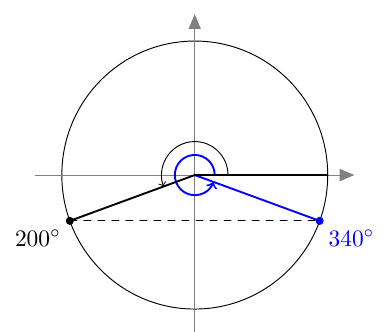
- Sama sinin arvo on kulmilla $200^\circ$ ja $340^\circ$.
Huom. kulma $200^\circ$ löydetään vähentämällä annetusta kulmasta yksi täysi kierros.
Kosini
Merkitse kulma $\beta$ yksikköympyrään ja päättele, millä välin $[0^\circ, 360^\circ \pe$ kulmilla on sama kosinin arvo kuin kulmalla $\beta$.
- $\beta = 1210^\circ$
- $\beta = -400^\circ$
Vinkki: tutki ensin, kuinka monta täyttä kierrosta kulmaan $\beta$ sisältyy.
Vastaus
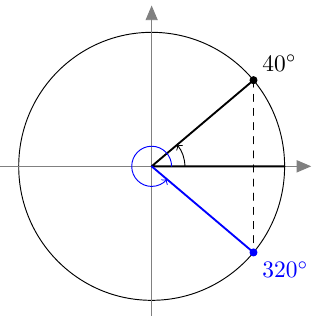
- Sama kosinin arvo on kulmilla $130^\circ$ ja $230^\circ$.
Huom. kulma $130^\circ$ löydetään vähentämällä annetusta kulmasta kolme täyttä kierrosta.

- Sama kosinin arvo on kulmilla $40^\circ$ ja $320^\circ$.
Huom. kulma $320^\circ$ löydetään lisäämällä annettuun kulmaan kaksi täyttä kierrosta.
Sini
Tässä tehtävässä määritetään kulmien $30^\circ$, $150^\circ$, $210^\circ$ ja $330^\circ$ sinin tarkka arvo.
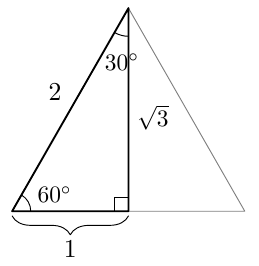
- Päättele alla olevan muistikolmion avulla, mitä on $\sin 30^\circ$.
- Merkitse kulmat $30^\circ$, $150^\circ$, $210^\circ$ ja $330^\circ$ yksikköympyrään.
- Päättele yksikköympyrän avulla, mitä ovat $\sin 150^\circ$, $\sin 210^\circ$ ja $\sin 330^\circ$.
Vastaus
- $\sin 30^\circ = \frac{1}{2}$
- Kulmat yksikköympyrässä:
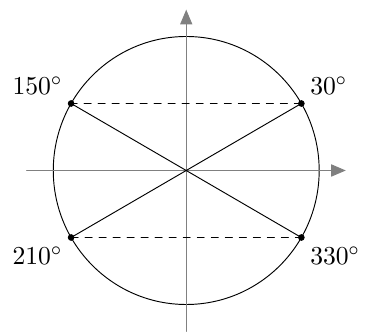
- $$\sin 30^\circ = \frac{1}{2} = \sin 150^\circ$$ ja $$\sin 210^\circ = -\frac{1}{2} = \sin 330^\circ$$
Kosini
Tässä tehtävässä määritetään kulmien $45^\circ$, $135^\circ$, $225^\circ$ ja $315^\circ$ kosinin tarkka arvo.
- Päättele alla olevan muistikolmion avulla, mitä on $\cos 45^\circ$.
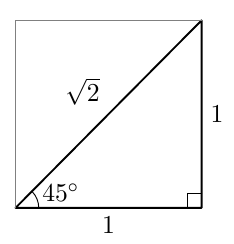
- Merkitse kulmat $45^\circ$, $135^\circ$, $225^\circ$ ja $315^\circ$ yksikköympyrään.
- Päättele yksikköympyrän avulla, mitä ovat $\cos 135^\circ$, $\cos 225^\circ$ ja $\cos 315^\circ$.
Vastaus
- $\cos 45^\circ = \frac{1}{\sqrt{2}}$
- Kulmat yksikköympyrässä:
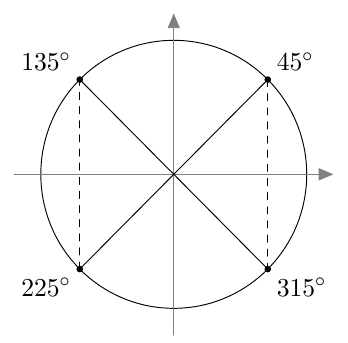
- $$\cos 45^\circ = \frac{1}{\sqrt{2}} = \cos 315^\circ$$ ja $$\cos 135^\circ = -\frac{1}{\sqrt{2}} = \cos 225^\circ$$
Sini ja kosini
Tehtävänä on määrittää lausekkeen $$ \sin \left(\frac{\alpha}{2}\right) + \cos \left(\frac{\alpha}{5}\right) $$ arvo, jos $\alpha = 600^\circ$.
- Päättele tarkka arvo alla olevan muistikolmion ja yksikköympyrän avulla.

- Laske likiarvo laskimen avulla ja anna vastaus neljän merkitsevän numeron tarkkuudella.
Vastaus
- \begin{align*} \sin 300^\circ + \cos 120^\circ &= -\frac{\sqrt{3}}{2} - \frac{1}{2} \\ &= \frac{-1-\sqrt{3}}{2} \end{align*}
- Likiarvo on $-1{,}366$.
Sini ja kosini
Ratkaise yhtälö $$ \sin \alpha \cos \alpha = 0. $$ Vinkki: palauta tarvittaessa mieleesi MAA2-kurssin teoreema 4.
Vastaus
$\alpha = n\cdot 90^\circ$, missä $n$ on kokonaisluku (tulon nollasäännön nojalla yhtälö toteutuu, jos ja vain jos $\sin \alpha = 0$ tai $\cos \alpha = 0$).
Sini ja kosini
Ratkaise yhtälöt
- $\sin^2 \alpha = 1$
- $\cos^2 \alpha = \frac{1}{2}.$
Varmista yksikköympyrän avulla, että huomaat kaikki mahdolliset ratkaisut.
Vastaus
- $\alpha = 90^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
Huom. alkuperäinen yhtälö toteutuu, jos ja vain jos $\sin \alpha = 1$ tai $\sin \alpha = -1$. - $\alpha = 45^\circ + n \cdot 90^\circ$, missä $n$ on kokonaisluku.
Huom. alkuperäinen yhtälö toteutuu, jos ja vain jos $\cos \alpha = \frac{1}{\sqrt{2}}$ tai $\cos \alpha = -\frac{1}{\sqrt{2}}$.
Sini ja kosini
Määritä kulman $\alpha$ kosinin tarkka arvo, jos
- $\sin \alpha = \dfrac{2}{3}$ ja kulma $\alpha$ on tylppä
- $\sin \alpha = -\dfrac{4}{5}$ ja $-90^\circ < \alpha < 90^\circ$.
Vastaus
- $\cos \alpha = -\dfrac{\sqrt{5}}{3}$
- $\cos \alpha = \dfrac{3}{5}$
Sini ja kosini
Sievennä lauseke:
- $\cos^3\! \alpha + \cos \alpha \sin^2\! \alpha$
- $(\sin \alpha + \cos \alpha)^2$.
Vinkki: teoreema 7.
Vastaus
- $\cos \alpha$
- $1 + 2\sin \alpha \cos \alpha$
Sini ja kosini
Ratkaise yhtälö $$ 5 - 7\sin \alpha - 2\cos^2\! \alpha = 0. $$ Vinkki: teoreema 7.
Vastaus
$\alpha = 30^\circ + n \cdot 360^\circ$ tai $\alpha = 150^\circ + n \cdot 360^\circ$.
Sini
Tehtävänä on ratkaista yhtälö $$ \sin 2\alpha = \sin \alpha. $$
- Merkitse yksikköympyrään jokin kulma $\alpha$, jonka kehäpiste ei ole koordinaattiakselilla.
- Merkitse yksikköympyrään muut kulmat, joilla on sama sinin arvo kuin a-kohdan kulmalla. Ilmaise ne kulman $\alpha$ avulla.
- Muodosta b-kohdan avulla kaksi yhtälöä kulmalle $2\alpha$.
- Mikä on yhtälön $\sin 2\alpha = \sin \alpha$ ratkaisu?
Vastaus
-
- Kulmat ovat $\alpha + n \cdot 360^\circ$ ja $180^\circ - \alpha + n \cdot 360^\circ$:
- Yhtälö $\sin 2\alpha = \sin \alpha$ toteutuu, jos ja vain jos $$ 2\alpha = \alpha + n \cdot 360^\circ $$ tai $$ 2\alpha = 180^\circ - \alpha + n \cdot 360^\circ, $$ missä $n$ on kokonaisluku.
- Yhtälö $\sin 2\alpha = \sin \alpha$ toteutuu, jos ja vain jos $$ \alpha = n \cdot 360^\circ $$ tai $$ \alpha = 60^\circ + n \cdot 120^\circ, $$ missä $n$ on kokonaisluku.
Sini ja kosini
Ratkaise yhtälöt
- $\sin 3\alpha = \sin \alpha$
- $\cos 3\alpha = \cos 2\alpha$
Vastaus
- $$ \alpha = n \cdot 180^\circ $$ tai $$ \alpha = 45^\circ + n \cdot 90^\circ, $$ missä $n$ on kokonaisluku.
- $$ \alpha = n \cdot 72^\circ, $$ missä $n$ on kokonaisluku.
Huom. tämä sisältää myös ratkaisut, joissa $\alpha = n \cdot 360^\circ$.
Kosini
Tehtävänä on ratkaista yhtälö $$ \cos (20^\circ - \alpha) = \cos \alpha. $$
- Merkitse yksikköympyrään jokin kulma $\alpha$, jonka kehäpiste ei ole koordinaattiakselilla.
- Merkitse yksikköympyrään muut kulmat, joilla on sama kosinin arvo kuin a-kohdan kulmalla. Ilmaise ne kulman $\alpha$ avulla.
- Muodosta b-kohdan avulla kaksi yhtälöä kulmalle $20^\circ - \alpha$.
- Mikä on yhtälön $\cos (20^\circ - \alpha) = \cos \alpha$ ratkaisu?
Vastaus
-

- Kulmat ovat $\alpha + n \cdot 360^\circ$ ja $- \alpha + n \cdot 360^\circ$:
- Yhtälö $\cos (20^\circ - \alpha) = \cos \alpha$ toteutuu, jos ja vain jos $$ 20^\circ - \alpha = \alpha + n \cdot 360^\circ $$ tai $$ 20^\circ - \alpha = - \alpha + n \cdot 360^\circ, $$ missä $n$ on kokonaisluku.
- Yhtälö $\cos (20^\circ - \alpha) = \cos \alpha$ toteutuu, jos ja vain jos $$ \alpha = 10^\circ + n \cdot 180^\circ, $$ missä $n$ on kokonaisluku.
Sini
Ratkaise yhtälö $$ \sin (4\alpha + 75^\circ) = \sin \alpha. $$
Vastaus
- $$ \alpha = -25^\circ + n \cdot 120^\circ $$ tai $$ \alpha = 21^\circ + n \cdot 72^\circ, $$ missä $n$ on kokonaisluku.
- $$ \alpha = n \cdot 72^\circ, $$ missä $n$ on kokonaisluku.
Huom. tämä sisältää myös ratkaisut, joissa $\alpha = n \cdot 360^\circ$.
Tangentti
Tässä tehtävässä määritetään kulmien $60^\circ$, $120^\circ$, $240^\circ$ ja $300^\circ$ tangentin tarkka arvo.
- Päättele alla olevan muistikolmion avulla, mitä on $\tan 60^\circ$.

- Merkitse kulmat $60^\circ$, $120^\circ$, $240^\circ$ ja $300^\circ$ yksikköympyrään. Piirrä näkyviin myös suora $x = 1$ ja kulmien tangenttipisteet.
- Päättele b-kohdan kuvan avulla, mitä ovat $\tan 120^\circ$, $\tan 240^\circ$ ja $\tan 300^\circ$.
Vastaus
- $\tan 60^\circ = \sqrt{3}$
- Kulmat yksikköympyrässä:
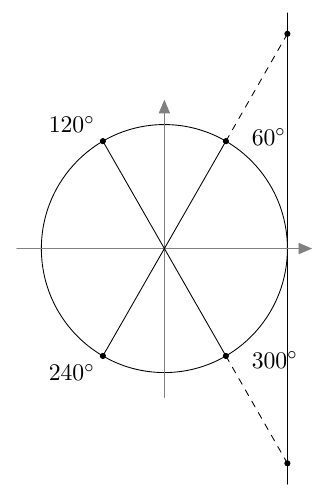
- $$\tan 60^\circ = \sqrt{3} = \tan 240^\circ$$ ja $$\tan 120^\circ = -\sqrt{3} = \tan 300^\circ$$
Tangentti
Määritä kulman $\alpha$ tangentti, kun tiedetään, että $$ \sin \alpha = -\frac{45}{53} $$ ja $$ \cos \alpha = -\frac{28}{53}. $$ Missä neljänneksessä kulman $\alpha$ kehäpiste sijaitsee?
Vastaus
Kulman kehäpiste on III neljänneksessä ja $\tan \alpha = \dfrac{45}{28}$.
Tangentti
Ratkaise yhtälöt asteen kymmenesosan tarkkuudella:
- $\tan \alpha = 2{,}5$
- $\tan 3\alpha = -6$
Vastaus
- $\alpha \approx 68{,}2^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha \approx -26{,}8^\circ + n \cdot 60^\circ$, missä $n$ on kokonaisluku.
Tangentti
Tiedetään, että $\tan \alpha = -2$ ja $\cos \alpha = \dfrac{1}{\sqrt{5}}$. Mikä on kulman $\alpha$ sinin tarkka arvo?
Vastaus
$\sin \alpha = -\dfrac{2}{\sqrt{5}}$
Tangentti
Ratkaise yhtälö
- $\sin \alpha = \cos \alpha$
- $\sin \alpha + \sqrt{3}\cos \alpha = 0$
Vastaus
- $\alpha = 45^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
- $\alpha = 120^\circ + n \cdot 180^\circ$, missä $n$ on kokonaisluku.
Tangentti
Tiedetään, että $\tan \alpha = 4$ ja $180^\circ < \alpha < 360^\circ$. Tehtävänä on määrittää kulman $\alpha$ sinin ja kosinin tarkat arvot.
- Hahmottele kulma $\alpha$ yksikköympyrään. Missä neljänneksessä sen kehäpiste sijaitsee?
- Piirrä suorakulmainen kolmio. Valitse sen kateettien pituudet niin, että kolmion toisen terävän kulman $\beta$ tangentti on 4. Mikä on tällöin hypotenuusan pituus?
- Määritä b-kohdan suorakulmaisen kolmion avulla $\sin \beta$ ja $\cos \beta$.
- Päättele yksikköympyrän avulla, mitä ovat $\sin \alpha$ ja $\cos \alpha$.
Vastaus
- Kulman $\alpha$ kehäpiste on III neljänneksessä, koska $180^\circ < \alpha < 360^\circ$ ja tangentin arvo on positiivinen.
- Kateettien pituudet 1 ja 4, hypotenuusan pituus $\sqrt{17}$
- $\sin \beta = \dfrac{4}{\sqrt{17}}\ $ ja $\ \cos \beta = \dfrac{1}{\sqrt{17}}$.
- $\sin \alpha = -\dfrac{4}{\sqrt{17}}\ $ ja $\ \cos \alpha = -\dfrac{1}{\sqrt{17}}$.
Tangentti
Kulma $\alpha$ toteuttaa yhtälön $$ 5\sin \alpha + 7\cos\alpha = 0. $$ Määritä kulman $\alpha$ sinin ja kosinin tarkat arvot.
Vastaus
Kulman $\alpha$ tangentin arvoksi saadaan $\tan \alpha = -\dfrac{7}{5}$. Tästä voidaan päätellä, että kulma on II tai IV neljänneksessä. Sinin ja kosinin arvoiksi saadaan $$ \sin \alpha = \frac{7}{\sqrt{74}} \ \text{ ja } \ \cos \alpha = -\frac{5}{\sqrt{74}} $$ tai $$ \sin \alpha = -\frac{7}{\sqrt{74}} \ \text{ ja } \ \cos \alpha = \frac{5}{\sqrt{74}} $$
Tangentti
Tehtävänä on ratkaista yhtälö $$ \tan 3\alpha = \tan \alpha. $$
- Mitä ovat ne kulmat $\alpha$, joilla lauseke $\tan \alpha$ ei ole määritelty?
- Mitä ovat ne kulmat $\alpha$, joilla lauseke $\tan 3\alpha$ ei ole määritelty?
- Merkitse yksikköympyrään jokin kulma $\alpha$, jonka kehäpiste ei ole koordinaattiakselilla.
- Merkitse yksikköympyrään muut kulmat, joilla on sama tangentin arvo kuin c-kohdan kulmalla. Ilmaise ne kulman $\alpha$ avulla.
- Muodosta d-kohdan avulla yhtälö kulmalle $3\alpha$.
- Mikä on yhtälön $\tan 3\alpha = \tan \alpha$ ratkaisu? Ota huomioon a- ja b-kohtien määrittelyehdot.
Vastaus
- Lauseke $\tan \alpha$ ei ole määritelty, jos $\alpha = 90^\circ + n \cdot 180^\circ$.
- Lauseke $\tan 3\alpha$ ei ole määritelty, jos $\alpha = 30^\circ + n \cdot 60^\circ$.
-

- Kulmat ovat $\alpha + n \cdot 180^\circ$:
- Yhtälö $\tan 3\alpha = \tan \alpha$ toteutuu, jos ja vain jos $$ 3\alpha = \alpha + n \cdot 180^\circ, $$ missä $n$ on kokonaisluku.
- Yhtälö $\tan 3\alpha = \tan \alpha$ toteutuu, jos ja vain jos $$ \alpha = n \cdot 180^\circ, $$ missä $n$ on kokonaisluku.
Huom. Ratkaisuehdokkaiksi saadaan $\alpha = n \cdot 90^\circ$, missä $n$ kokonaisluku. Näistä määrittelyehto kuitenkin sulkee pois ne kulmat, joiden kehäpiste on $y$-akselilla.
TEHTÄVÄSARJA III
Ratkaise yhtälöt
- $\sin\left(\dfrac{x}{2}\right) = \dfrac{1}{\sqrt{2}}$
- $\cos 2x + \cos 3x = 0.$
[Pitkä S2009/2c & Pitkä K2013/9]
Vastaus
- $x = 90^\circ + 2n \cdot 360^\circ$ tai $x = 270^\circ + 2n \cdot 360^\circ$, missä $n$ on kokonaisluku.
- $x = (2n+1)\cdot 180^\circ$ tai $x = \dfrac{2n-1}{5}\cdot 180^\circ$, missä $n$ on kokonaisluku.
Millä vakion $a$ arvoilla yhtälöllä $$ \sin x = 5 - a^2\sin x $$ on ratkaisuja?
[Pitkä K2006/5]
Vastaus
Arvoilla $a \leq -2$ ja arvoilla $a \geq 2$.
Ratkaise yhtälöt
- $3\tan \left(\dfrac{x}{2}\right) + 3 = 0$
- $2\sin^2 \! x + 3\cos x - 3 = 0$
Vastaus
- $x = -90^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
- $x = n \cdot 360^\circ$ tai $x = \pm 60^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
Huvipuiston maailmanpyörän halkaisija on 34 metriä ja sen keskipiste on 18 metrin korkeudessa. Pyörä pyörähtää yhden kierroksen minuutissa.
- Muodosta lauseke, joska ilmaisee, millä korkeudella maailmanpyörän vaunu on $t$ sekuntia sen jälkeen, kun se on ylöspäin mennessään ollut pyörän keskipisteen tasalla.
- Minä ajanhetkinä vaunu on 25 metrin korkeudessa? Anna vastaukset sekunnin tarkkuudella.
Vastaus
- $18 \text{ m } + 17 \text{ m } \cdot \sin (t \cdot 6^\circ)$
- Noin 4 sekunnin ja 26 sekunnin kuluttua siitä, kun vaunu on ylöspäin mennessään ollut pyörän keskipisteen tasalla.
Osoita, että lausekkeen $$ (\sin \alpha + \cos \alpha)^2 + (\sin\alpha - \cos\alpha)^2 $$ arvo ei riipu kulmasta $\alpha$.
Vastaus
Lauseke sievenee muotoon $$ 1 + 2\sin\alpha\cos\alpha + 1 - 2\sin\alpha\cos\alpha = 2. $$
Tiedetään, että kulma $\alpha$ toteuttaa yhtälön $$ 4\sin x + 3\cos x = 0. $$ Määritä lausekkeen $3\sin \alpha + 2\cos\alpha$ arvo.
Vastaus
Lausekkeen arvo on joko $\frac{1}{5}$, jos kulma $\alpha$ on II neljänneksessä, tai $-\frac{1}{5}$, jos kulma $\alpha$ on IV neljänneksessä.
Osoita, että $$ \frac{1}{\cos^2\, \alpha} - \tan^2\, \alpha = 1 $$ kaikilla kulmilla $\alpha$.
Vastaus
Sievennetään: \begin{align*} \frac{1}{\cos^2\, \alpha} - \tan^2\, \alpha &= \frac{1}{\cos^2\, \alpha} - \left(\frac{\sin\alpha}{\cos \alpha}\right)^2 \\[2mm] &= \frac{1 - \sin^2\! \alpha}{\cos^2\, \alpha} \\[2mm] &= \frac{\cos^2\! \alpha}{\cos^2\, \alpha} = 1 \end{align*}
Määritä kaikki kulmat $\beta$, joiden
- sini on yhtä suuri kuin kulman $\alpha$ sinin vastaluku
- kosini on yhtä suuri kuin kulman $\alpha$ kosinin vastaluku.
Ilmoita vastauksessa kulmat $\beta$ kulman $\alpha$ avulla.
Vinkki: hahmottele kulma $\alpha$ yksikköympyrään ja päättele sen avulla, missä kulman $\beta$ kehäpiste voi sijaita.
Vastaus
- Sopivat kulmat ovat $\beta = -\alpha + n \cdot 360^\circ$ ja $\beta = 180^\circ + \alpha + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
- Sopivat kulmat ovat $\beta = 180^\circ -\alpha + n \cdot 360^\circ$ ja $\beta = \alpha - 180^\circ + n \cdot 360^\circ$, missä $n$ on kokonaisluku.
Ratkaise yhtälö $$ \left(\sin \alpha + \sqrt{3}\right)^2 = \frac{27}{4} $$ [Pitkä K1987/4]
Vastaus
$\alpha = 60^\circ + n \cdot 360^\circ$ tai $\alpha = 120^\circ + n \cdot 360^\circ$
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.