Derivointisääntöjä I
Luvun tavoitteet
Tämän luvun tavoitteena on, että pystyt määrittämään derivaatan erotusosamäärän raja-arvona ja derivoit polynomifunktiot sujuvasti derivointisääntöjen avulla. Osaat
- muodostaa funktion erotusosamäärän ja laskea sen raja-arvon
- määrittää vakiofunktion ja potenssifunktioiden derivaattafunktiot
- käyttää funktioiden summan ja vakiolla kerrotun funktion derivointisääntöjä
- muodostaa polynomifunktion kuvaajalle asetetun tangentin yhtälön.
Derivaatan määritelmä
Kurssin ensimmäisessä luvussa tutustuimme funktion derivaatan käsitteeseen. Opimme, että funktion derivaatta on funktion kuvaajalle piirretyn tangentin kulmakerroin, joka kuvaa funktion kasvunopeutta kyseisessä kohdassa. Tässä kappaleessa määrittelemme derivaatan käsitteen täsmällisemmin tietynlaisena raja-arvona.
Tarkastellaan aluksi funktiota $f$ ja suoraa, joka leikkaa funktion kuvaajan (ainakin) kahdessa kohdassa kuten alla olevassa kuvassa.
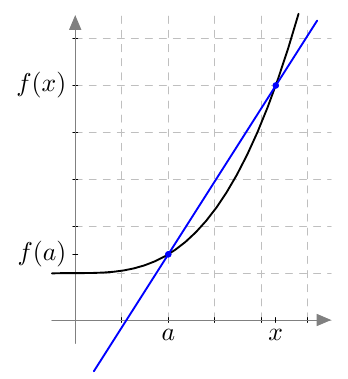 Tämän suoran kulmakerroin on $$ \frac{f(x) - f(a)}{x-a} $$ Sitä sanotaan funktion $f$ erotusosamääräksi kohdassa $a$.
Tämän suoran kulmakerroin on $$ \frac{f(x) - f(a)}{x-a} $$ Sitä sanotaan funktion $f$ erotusosamääräksi kohdassa $a$.
Kun $x \rightarrow a$, lähestyy pisteiden $(a,f(a))$ ja $(x, f(x))$ kautta kulkeva suora funktion kuvaajalle pisteeseen $(a,f(a))$ piirrettyä tangettia:
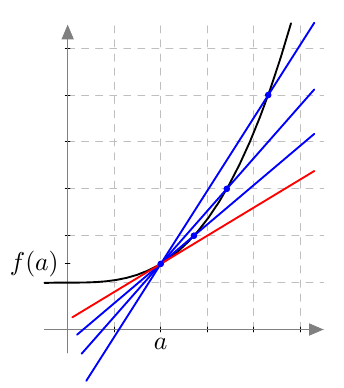
Suoran kulmakerroin puolestaan lähestyy tangentin kulmakerrointa, joten seuraava määritelmä sopii derivaatan täsmälliseksi määritelmäksi:
MÄÄRITELMÄ: DERIVAATTA
Jos funktion $f$ erotusosamäärällä kohdassa $a$ on raja-arvo kohdassa $a$, niin funktio $f$ on derivoituva kohdassa $a$.
Raja-arvoa kutsutaan funktion $f$ derivaataksi kohdassa $a$ ja merkitään $f'(a)$. Siis $$ f'(a) = \lim_{x \rightarrow a} \frac{f(x)-f(a)}{x-a} $$
Esimerkiksi funktion $f(x) = x^2$ erotusosamäärä kohdassa $0{,}5$ on $$ \frac{x^2 - 0{,}5^2}{x-0{,}5} $$ Murtolauseketta voidaan muokata niin, että raja-arvo on mahdollista selvittää: \begin{align*} \frac{x^2 - 0{,}5^2}{x-0{,}5} &= \frac{(x - 0{,}5)(x + 0{,}5)}{x-0{,}5} \\[2mm] &= x + 0{,}5 \xrightarrow[x \rightarrow 0{,}5]{} 0{,}5 + 0{,}5 \\ &= 1 \end{align*} Siis funktion $f(x) = x^2$ derivaatta kohdassa $x = 0{,}5$ on $$f'(0{,}5) = 1.$$ 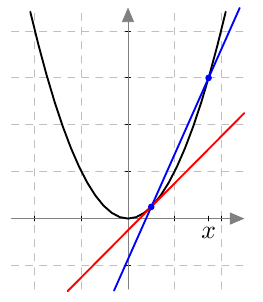
Derivaatan määritelmä
Tehtävänä on määrittää funktion $f(x) = x^2$ derivaatan arvo kohdassa $3$.
- Muodosta funktion $f$ erotusosamäärä kohdassa $3$.
- Muokkaa erotusosamäärää niin, että supistaminen on mahdollista. Mikä on erotusosamäärän raja-arvo, kun $x \rightarrow 3$?
- Mitä on $f'(3)$?
VASTAUS
- $\dfrac{x^2 - 9}{x-3}$
- ${\displaystyle x + 3 \xrightarrow[x\rightarrow 3]{} 6}$
- $f'(3) = 6$
Derivaatan määritelmä
Tehtävänä on määrittää funktion $$g(x) = \dfrac{1}{x-2}$$ derivaatan arvo kohdassa $-1$.
- Muodosta funktion $g$ erotusosamäärä kohdassa $-1$.
- Sievennä erotusosamäärä mahdollisimman pitkälle. Aloita laventamalla osoittajassa esiintyvät termit samannimisiksi.
- Mitä on $g'(-1)$?
VASTAUS
- $\dfrac{\frac{1}{x-2} + \frac{1}{3}}{x+1}$
- ${\displaystyle \frac{1}{3(x-2)}}$
- $f'(-1) = -\frac{1}{9}$
Derivaatan arvon selvittäminen suoraan derivaatan määritelmän perusteella on monesti melko työlästä. Sen vuoksi seuraavaksi johdetaan sääntöjä, joilla voidaan helpommin muodostaa erilaisten funktioiden derivaattoja.
Vakiofunktio ja potenssifunktiot
Kurssissa MAA2 tutustuttiin potenssifunktioihin. Potenssifunktiot ovat muotoa $f(x) = x^n$, missä $n$ on positiivinen kokonaisluku. Tässä kappaleessa määritetään potenssifunktioiden sekä vakiofunktion derivaattafunktiot.
Tarkastellaan aluksi ensimmäisen asteen potenssifunktiota $f(x) = x$. Sen erotusosamäärä kohdassa $a$ on $$\frac{f(x)-f(a)}{x-a} = \frac{x-a}{x-a} = 1.$$ Funktion derivaatta kohdassa $a$ on erotusosamäärän raja-arvo: $$ f'(a) = \lim_{x \rightarrow a} 1 = 1. $$ Tulos ei riipu tarkastelukohdasta $a$, joten derivaattafunktio vakiofunktio $f'(x) = 1$. Tämä nähdään myös ensimmäisen asteen potenssifunktion kuvaajasta:
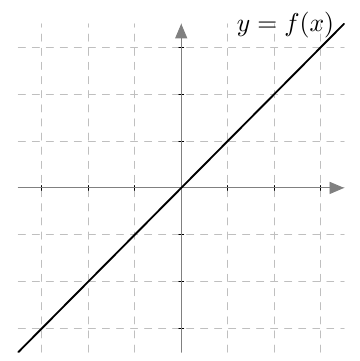
Kuvaaja on suora, jonka kulmakerroin on $1$. Funktion arvojen kasvunopeus on siis koko ajan $1$.
Vakiofunktion derivaattafunktio
Tarkastellaan vakiofunktiota $g(x) = \pi$.
- Muodosta funktion $g$ erotusosamäärä kohdassa $a$.
- Määritä funktion $g$ derivaatta kohdassa $a$ erotusosamäärän raja-arvona.
- Riippuuko derivaatan arvo tarkastelukohdasta? Mikä on vakiofunktion derivaattafunktio?
- Tarkista johtopäätöksesi funktion $g$ kuvaajan avulla. Mikä on sen perusteella funktion arvojen kasvunopeus?
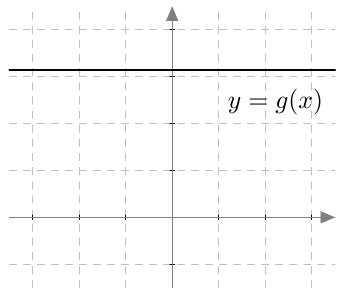
VASTAUS
- $\dfrac{\pi - \pi}{x-a} = \dfrac{0}{x-a} = 0$
- ${\displaystyle g'(a) = \lim_{x \rightarrow a} 0 = 0}$
- Vakiofunktion derivaattafunktio on nollafunktio $g'(x) = 0$
- Funktion arvojen kasvunopeus on $0$.
Edellisen tehtävän päättely voidaan toistaa minkä tahansa vakiofunktion tapauksessa, joten saadaan seuraava teoreema:
TEOREEMA
Vakiofunktion $f(x) = c$ derivaattafunktio nollafunktio: $$f'(x) = 0.$$
Perustelu kuten tehtävässä 4.3.
Toisen asteen potenssifunktion derivaattafunktio
Tehtävänä on määrittää toisen asteen potenssifunktion $f(x) = x^2$ derivaattafunktio.
- Muodosta funktion $f$ erotusosamäärä kohdassa $a$.
- Muokkaa erotusosamäärää niin, että supistaminen on mahdollista. Mikä on erotusosamäärän raja-arvo, kun $x \rightarrow a$?
- Mikä on toisen asteen potenssifunktion $f(x) = x^2$ derivaattafunktio?
VASTAUS
- $\dfrac{x^2 - a^2}{x-a}$
- ${\displaystyle x+a \xrightarrow[x \rightarrow a]{} a + a = 2a}$
- Derivaattafunktio on $f'(x) = 2x$.
Kolmannen asteen potenssifunktion derivaattafunktio
Tehtävänä on määrittää kolmannen asteen potenssifunktion $f(x) = x^3$ derivaattafunktio.
- Muodosta funktion $f$ erotusosamäärä kohdassa $a$.
- Kerro sulut auki lausekkeesta $(x-a)(x^2 + xa + a^2)$.
- Sievennä erotusosamäärää b-kohdan avulla. Mikä on erotusosamäärän raja-arvo, kun $x \rightarrow a$?
- Mikä on kolmannen asteen potenssifunktion $f(x) = x^3$ derivaattafunktio?
VASTAUS
- $\dfrac{x^3 - a^3}{x-a}$
- $(x-a)(x^2 + xa + a^2) = x^3 - a^3$
- ${\displaystyle x^2 + xa + a^2 \xrightarrow[x \rightarrow a]{} 3a^2}$
- $f'(x) = 3x^2$.
Edellisen tehtävän idea voidaan yleistää myös korkeamman asteen potenssifunktioille. Jos $n \geq 2$ on positiivinen kokonaisluku, niin \begin{align*} (x-a)(x^{n-1} + x^{n-2}a + \cdots + xa^{n-2} &+ a^{n-1}) \\[1mm] &= x^n - a^n \end{align*} Tämän yhtälön avulla erotusosamäärä saadaan supistettua niin, että raja-arvo voidaan määrittää.
TEOREEMA
Olkoon $n$ positiivinen kokonaisluku. Potenssifunktion $f(x) = x^n$ derivaattafunktio on $$f'(x) = nx^{n-1}.$$
Perustelu: Aikaisemmin on osoitettu, että teoreeman tulos pätee tapauksessa $n = 1$. Nimittäin funktion $f(x) = x$ derivaattafunktio on $$f'(x) = 1 = 1 \cdot x^0.$$ Oletetaan seuraavaksi, että $n \geq 2$. Funktion $f(x) = x^n$ erotusosamäärä kohdassa $a$ on $$ \frac{x^n-a^n}{x-a}. $$ Se supistuu muotoon $$x^{n-1} + x^{n-2}a + \cdots + xa^{n-2} + a^{n-1}.$$ Tässä summassa muuttujan $x$ eksponentti saa kaikki kokonaislukuarvot luvusta $n-1$ lukuun $0$, joten yhteenlaskettavia on $n$ kappaletta. Vakion $a$ eksponentti saa vastaavat arvot niin, että jokaisessa yhteenlaskettavassa eksponenttien summa on aina $n-1$. Kun $x \rightarrow a$, raja-arvoksi saadaan \begin{align*} &\phantom{={}} a^{n-1} + a^{n-2}a + \cdots + aa^{n-2} + a^{n-1} \\[1mm] &= a^{n-1} + a^{n-1} + \cdots + a^{n-1} + a^{n-1} \\[1mm] &= na^{n-1} \end{align*} Siis $$f'(a) = na^{n-1}.$$ Tästä voidaan päätellä, että potenssifunktio $f(x) = x^n$ on derivoituva ja sen derivaattafunktio on $f'(x) = nx^{n-1}$.
Derivaattafunktio voidaan ilmaista myös derivointimerkin $\mathop{\mathrm{D}}$ avulla. Esimerkiksi tehtävissä 4.3-4.5 osoitettiin, että \begin{align*} \mathop{\mathrm{D}} \pi &= 0 \\ \mathop{\mathrm{D}} x^2 &= 2x \\ \mathop{\mathrm{D}} x^3 &= 3x^2 \end{align*} Seuraavassa tehtävässä harjoitellaan teoreeman 2 soveltamista.
Derivaattafunktio
Määritä seuraavat derivaattafunktiot:
- $\mathop{\mathrm{D}} x^5$
- $\mathop{\mathrm{D}} x^9$
- $\mathop{\mathrm{D}} x^{14}$
- $\mathop{\mathrm{D}} 9$
Kertaa tarvittaessa tehtävä 4.3.
VASTAUS
- $\mathop{\mathrm{D}} x^5 = 5x^4$
- $\mathop{\mathrm{D}} x^9 = 9x^8$
- $\mathop{\mathrm{D}} x^{14} = 14x^{13}$
- $\mathop{\mathrm{D}} 9 = 0$
Funktioiden summa ja vakiokerroin
Edellisessä kappaleessa tutkitiin potenssifunktioita ja vakiofunktioita. Polynomifunktiot saadaan muodostettua niistä yhteenlaskun ja vakiolla kertomisen avulla. Esimerkiksi polynomifunktio $$ p(x) = -3x^2 + 5x - 4 $$ voidaan muodostaa potenssifunktioista $f(x) = x^2$ ja $g(x) = x$ sekä vakiofunktiosta $h(x) = -4$: $$ p(x) = -3f(x) + 5g(x) + h(x). $$ Tässä kappaleessa osoitetaan, että derivaattafunktio on vastaava yhdistelmä potenssi- ja vakiofunktioiden derivaatoista: $$ p'(x) = -3f'(x) + 5g'(x) + h'(x). $$
Derivaattafunktio
Sievennä funktion $p(x) = -3x^2 + 5x - 4$ derivaattafunktio $$p'(x) = -3f'(x) + 5g'(x) + h'(x),$$ missä $f(x) = x^2$, $g(x) = x$ ja $h(x) = -4$.
VASTAUS
$p'(x)= -6x + 5$
Tarkastellaan aluksi funktioiden summan derivaattaa. Seuraavassa teoreemassa osoitetaan, että se saadaan laskemalla funktioiden derivaatat yhteen. Lue teoreema ja sen perustelu huolellisesti ja mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Oletetaan, että funktiot $f$ ja $g$ ovat derivoituvia. Summan $f+g$ derivaatta on funktioiden $f$ ja $g$ derivaattojen summa: $$(f + g)'(x) = f'(x) + g'(x)$$ eli $$\mathop{\mathrm{D}}(f(x) + g(x)) = f'(x) + g'(x)$$
Perustelu: Summan $f+g$ erotusosamäärä kohdassa $a$ on $$ \frac{(f(x) + g(x)) - (f(a) + g(a))}{x-a}. $$ Muokataan tätä erotusmäärää niin, että siitä erottuvat funktioiden $f$ ja $g$ erotusosamäärät: \begin{align*} &\phantom{={}}\frac{(f(x) + g(x)) - (f(a) + g(a))}{x-a} \\[2mm] &= \frac{f(x) + g(x) - f(a) - g(a)}{x-a} \\[2mm] &= \frac{f(x) - f(a) + g(x) - g(a)}{x-a} \\[2mm] &= \frac{f(x) - f(a)}{x-a} + \frac{g(x) - g(a)}{x-a} \end{align*} Summan erotusosamäärä on siis funktioiden $f$ ja $g$ erotusosamäärien summa. Koska funktiot $f$ ja $g$ ovat derivoituvia, näillä erotusosamäärillä on raja-arvot: \begin{align*} \frac{f(x) - f(a)}{x-a} &+ \frac{g(x) - g(a)}{x-a} \\[1mm] &\xrightarrow[x \rightarrow a]{} f'(a) + g'(a) \end{align*} Näin on osoitettu, että $$(f+g)'(a) = f'(a) + g'(a).$$
Funktioiden summan derivaatta
Määritä seuraavat derivaattafunktiot teoreeman 3 avulla:
- $\mathop{\mathrm{D}} (x^4 + x)$
- $\mathop{\mathrm{D}} (x^7 + x^2 - 25)$
VASTAUS
- $\mathop{\mathrm{D}} (x^4 + x) = 4x^3 + 1$
- $\mathop{\mathrm{D}} (x^7 + x^2 - 25) = 7x^6 + 2x$
Funktioiden summan derivaatta
Tutkitaan funktiota $f(x) = x^2 + x$.
- Määritä derivaattafunktio $f'(x)$.
- Mikä on funktion $f$ arvojen kasvunopeus kohdassa $x = 1$?
- Missä kohdassa funktion arvojen kasvunopeus on nolla?
- Mikä on funktion kuvaajalle kohtaan $x = -2$ piirretyn tangentin kulmakerroin?
- Mikä on funktion kuvaajalle kohtaan $x = -2$ piirretyn tangentin yhtälö?
Piirrä funktion $f$ kuvaaja ja vertaa vastauksiasi siihen. Ovatko vastaukset järkeviä?
VASTAUS
- $f'(x) = 2x + 1$.
- $f'(1) = 3$.
- $x = -\frac{1}{2}$
- $f'(-2) = -3$.
- $y = -3x-4$
Tarkastellaan seuraavaksi vakiolla kerrotun funktion derivaattaa. Kun funktio kerrotaan vakiolla, tulee sen arvo jokaisessa kohdassa kerrotuksi tällä vakiolla:
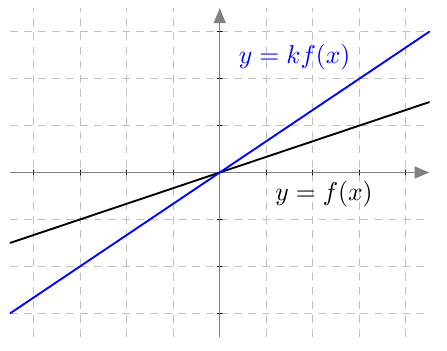
Vakiolla kerrottu funktio
Funktioiden $f$ ja $kf$ kuvaajat näkyvät yllä olevassa kuvassa. Mikä on vakion $k$ arvo tässä tapauksessa?
VASTAUS
$k = 2$
Vakiolla kerrotun funktion derivaatta
Oletetaan, että funktio $f$ on derivoituva. Tehtävänä on määrittää vakiolla kerrotun funktion $kf$ derivaatta.
- Muodosta funktion $kf$ erotusosamäärä kohdassa $a$.
- Muokkaa erotusosamäärää niin, että siitä erottuu funktion $f$ erotusosamäärä.
- Mikä on funktion $kf$ erotusosamäärän raja-arvo, kun $x \rightarrow a$?
VASTAUS
- $\dfrac{kf(x) - kf(a)}{x-a}$
- $k\cdot \dfrac{f(x) - f(a)}{x-a}$
- $kf'(a)$
Tehtävän 4.11 tuloksena saadaan seuraava teoreema:
TEOREEMA
Oletetaan, että funktio $f$ on derivoituva. Vakiolla kerrotun funktion $kf$ derivaatta on funktion $f$ derivaatta kerrottuna samalla vakiolla: $$(kf)'(x) = kf'(x)$$ eli $$\mathop{\mathrm{D}} kf(x) = kf'(x).$$
Perustelu tehtävässä 4.11.
Vakiolla kerrotun funktion derivaatta
Määritä seuraavat derivaattafunktiot teoreemojen 3 ja 4 avulla:
- $\mathop{\mathrm{D}} 7x^9$
- $\mathop{\mathrm{D}} (2x^5 - 4x^3 + 6x)$
- $\mathop{\mathrm{D}} (17x^2 - 8x^6 - 56)$
VASTAUS
- $63x^8$
- $10x^4 - 12x^2 + 6$
- $34x - 48x^5$
Vakiolla kerrotun funktion derivaatta
Tutkitaan funktiota $$f(x) = \frac{3}{2}x^2 - 10x + 20.$$
- Määritä derivaattafunktio $f'(x)$.
- Muuttuvatko funktion $f$ arvot voimakkaammin kohdassa $x = 2$ vai kohdassa $x = 4$?
- Missä kohdassa funktion arvojen kasvunopeus on nolla?
- Harjoittele teknisen apuvälineen käyttöä derivointitehtävissä. Katso esimerkiksi tästä Texas Nspiren käyttöön ohjevideo ja ratkaise kohdat (a)-(c) teknisen apuvälineen avulla.
- Funktion $f$ kuvaaja on paraabeli. Määritä paraabelin huipun koordinaatit.
Piirrä funktion $f$ kuvaaja ja vertaa vastauksiasi siihen. Ovatko vastaukset järkeviä?
VASTAUS
- $f'(x) = 3x - 10$
- Arvot muuttuvat voimakkaammin kohdassa $x = 2$, jossa funktion kuvaajalle piirretyn tangentin kulmakerroin on $-4$.
- Kohdassa $x = \frac{10}{3}$.
- Huippu on $\left(\frac{10}{3}, \frac{10}{3}\right)$.
Tässä luvussa johdettujen derivointisääntöjen avulla voidaan nyt määrittää minkä tahansa polynomifunktion derivaatta. Tämä mahdollistaa myös monenlaisten geometristen ongelmien ratkaisemisen. Tarkastellaan esimerkiksi tilannetta, jossa halutaan määrittää käyrälle $y = x^2 - 4x + 5$ sellainen tangentti, joka kulkee pisteen $(1,-2)$ kautta.
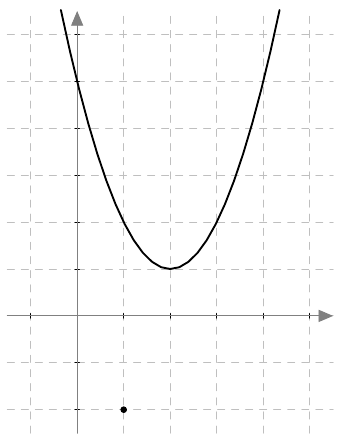
Havaitaan, että piste $(1,-2)$ ei ole käyrällä, sillä jos $x = 1$, niin $$ y = 1^2 - 4\cdot 1 + 5 = 2 \neq -2. $$ Hahmotellaan etsitty tangentti kuvaan ja merkitään sivuamispisteen $x$-koordinaattia kirjaimella $a$. Koska sivuamispiste on käyrällä, sen $y$-koordinaatti on käyrän yhtälön mukaisesti $a^2-4a+5$.
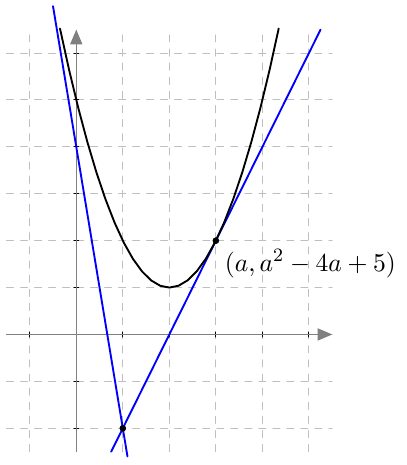
Kuvasta havaitaan, että sopivia tangentteja näyttäisi olevan kaksi erilaista. Tangentin kulmakerroin kohdassa $x = a$ saadaan derivoimalla käyrää vastaava polynomifunktio $f(x) = x^2 - 4x + 5$: $$ f'(x) = 2x - 4, $$ joten $$ f'(a) = 2a - 4. $$ Muodostetaan pisteen $(a,a^2-4a+5)$ kautta kulkevan tangentin yhtälö: $$ y - (a^2-4a+5) = (2a-4)(x-a) $$ Tangentti kulkee myös pisteen $(1,-2)$ kautta, joten saadaan yhtälö $$ -2 - (a^2-4a+5) = (2a-4)(1-a). $$ Tästä voidaan ratkaista $a$: \begin{align*} -2 - (a^2-4a+5) &= (2a-4)(1-a) \\ -a^2 + 4a - 7 &= 2a -2a^2 - 4 + 4a \\ a^2 - 2a - 3 &=0 \end{align*} Toisen asteen ratkaisukaavalla ratkaisuiksi saadaan \begin{align*} a &= \frac{2 \pm \sqrt{4+12}}{2} \\[2mm] &= \frac{2 \pm 4}{2} \\[2mm] &= 1\pm 2 \end{align*} Sopivia tangentteja siis todella on kaksi ja niiden yhtälöiksi saadaan arvoilla $a = -1$ ja $a = 3$ $$ y = -6x + 4 $$ ja $$ y = 2x - 4. $$
Käyrän tangentti
Määritä käyrälle $$ y = x^2 - x + 1 $$ kohtaan $x = -1$ piirretyn normaalin yhtälö.
VASTAUS
$y = \frac{1}{3}x + \frac{10}{3}$.
TEHTÄVÄSARJA II
Käyrän tangentti
Mihin paraabelin $$ y = x^2 - 2x $$ pisteeseen asetettu tangetti on suoran $$ 4x - y + 3 = 0 $$ suuntainen?
Vastaus
Pisteeseen $(3,3)$.
Käyrän tangentti
Määritä käyrälle $$ y = 4 + 3x - x^2 $$ kohtaan $x = 2$ piirretyn tangetin ja koordinaattiakselien rajoittaman kolmion pinta-ala.
Vastaus
Pinta-ala on 32.
Polynomifunktion derivaatta
Avain pudotetaan kerrostalon kolmannen kerroksen ikkunasta, joka on 15 metrin korkeudella maan pinnasta. Avaimen sijaintikorkeus ajan funktiona on likimain $$ f(t) = 15 - 4{,}9t^2. $$ Tässä aika ilmaistaan sekunteina ja sijaintikorkeus metreinä.
- Kuinka korkealla avain on 1,5 sekunnin kuluttua?
- Mikä on avaimen nopeus 1,5 sekunnin kuluttua?
Vinkki: nopeus on sijaintikorkeuden muutosnopeus eli derivaatta. - Millä nopeudella avain osuu maahan?
Pyöristä vastaukset kahden merkitsevän numeron tarkkuuteen.
Vastaus
- Noin 4,0 metrin korkeudella.
- Noin 15 m/s.
- Noin 17 m/s.
Polynomifunktion derivaatta
Pallo heitetään suoraan ylöspäin alkunopeudella 12 m/s, jolloin sen sijaintikorkeus ajan funktiona on likimain $$ f(t) = 12t - 4{,}9t^2. $$ Tässä aika ilmaistaan sekunteina ja sijaintikorkeus metreinä.
- Mikä on kappaleen nopeus 1 sekunnin kuluttua?
- Mikä on kappaleen nopeus 2 sekunnin kuluttua?
- Millä hetkellä kappale saavuttaa lentoratansa lakipisteen?
- Kuinka korkealla kappale käy?
Pyöristä vastaukset kahden merkitsevän numeron tarkkuuteen.
Vastaus
- Noin 2,2 m/s ylöspäin.
- Noin 7,6 m/s alaspäin.
- Noin 1,2 sekunnin kuluttua.
- Noin 7,3 metrin korkeudessa.
Polynomifunktion derivaatta
Lentokoneen lähtökiihdytyksessä kulkema matka ajan funktiona on likimain $$ s(t) = 1{,}05t^2. $$ Tässä aika ilmaistaan sekunteina ja matka metreinä.
- Mikä on lentokoneen nopeus $10$ sekunnin kuluttua? Anna vastaus sekä metreinä sekunnissa että kilometreinä tunnissa (käytä yksikkömuunnoksessa tarvittaessa apuna esimerkiksi Wikipediaa).
- Mikä on lentokoneen nopeus, kun se on liikkunut 500 metrin matkan?
- Kuinka pitkä kiitotien on vähintään oltava, jos koneen lentoonlähtönopeus on 250 km/h?
Pyöristä vastaukset kahden merkitsevän numeron tarkkuuteen.
Vastaus
- Noin 21 m/s eli noin 76 km/h.
- Noin $46$ m/s eli noin 165 km/h.
- Vähintään 1200 m (tässä vastauksen pyöristäminen normaalisääntöjen mukaan alaspäin ei tunnu turvallisuuden kannalta järkevältä).
Polynomifunktion derivaatta
Jos auton renkaat kaarteessa menettävät otteen tiehen, auto jatkaa matkaansa kaarteen tangetin suuntaisesti. Auto saapuu kaarteeseen $$ y = \frac{1}{2}\left(x - \frac{5}{2}\right)^2 + 2 $$ kovalla vauhdilla ylhäältä vasemmalta ja suistuu tieltä kohdassa $x = 2$.
- Missä pisteessä auto päätyy $x$-akselia pitkin virtaavaan jokeen?
- Kuinka pitkän matkan auto on kulkenut pitkin peltoa ennen jokeen suistumista? Koordinaatiston yksikkö vastaa kymmentä metriä maastossa.
Vastaus
- Pisteessä $\left(\frac{25}{4}, 0\right)$.
- Etäisyys on $\dfrac{17}{8}\sqrt{5} \approx 4{,}7$ eli noin 47 metriä.
Käyrän tangentti
Käyrän $$ y = \left(2 + \frac{x}{2}\right)\left(3- \frac{x}{2}\right) $$ ja $x$-akselin leikkauspisteisiin piirretyt tangentit rajoittavat yhdessä $x$-akselin kanssa kolmion. Laske tämän kolmion pinta-ala.
Vastaus
Pinta-ala on 62,5.
Käyrän tangetti
Määritä sen kulman suuruus, jonka käyrät $y = x^3$ ja $y = 2-x^2$ muodostavat leikkauspisteessään.
Huom. kahden käyrän välinen kulma on leikkauspisteeseen piirrettyjen tangenttien välinen kulma.
Vastaus
Käyrien välinen kulma on $45^\circ$.
(Leikkauspiste on $(1,1)$.)
Polynomifunktion derivaatta
Jos funktion lausekkeessa esiintyy useita kirjaimia, on oltava tarkkana sen suhteen, mikä niistä on muuttuja. Derivoi funktio
- $f(x) = tx^3-t^2x$
- $g(t) = tx^3-t^2x$
Vastaus
- $f'(x) = 3tx^2 - t^2$
- $g'(t) = x^3 - 2tx$
Polynomifunktion derivaatta
Tehtävänä on selvittää, minkä käyrän piirtää paraabelin $$ y = \frac{1}{2}x^2 + ax + a $$ huippu, kun $a$ saa kaikki reaalilukuarvot.
- Määritä paraabelin huipun koordinaatit.
- Ilmaise paraabelin huipun $y$-koordinaatti $x$-koordinaatin avulla. Millaisen käyrän yhtälö tällöin muodostuu?
Vastaus
- $\left(-a, -\frac{1}{2}a^2 + a\right)$.
- Paraabeli $y = -\frac{1}{2}x^2 - x$.
Huomaa, että a-kohdassa huipun $x$-koordinaatti on $-a$.
Käyrän tangentti
Määritä pisteestä $(1,-1)$ paraabelille $$ y = \frac{1}{2}x^2 - 1 $$ piirrettyjen tangettien yhtälöt.
Vastaus
$y = -1$ ja $y = 2x-3$.
Käyrän tangentti
Tehtävänä on osoittaa, että käyrät $y = x^2$ ja $$ y = -x^2 + 2x - \frac{1}{2} $$ sivuavat toisiaan.
- Määritä käyrien leikkauspisteet.
- Näytä, että käyrillä on yhdessä leikkauspisteessä yhteinen tangentti.
Vastaus
- Leikkauspisteitä on yksi: $\left(\frac{1}{2}, \frac{1}{4}\right)$.
- Kohdassa $x = \frac{1}{2}$ käyriä vastaavien polynomifunktioden derivaatan arvo on sama: \begin{align*} f'(0{,}5) &= 2\cdot 0{,}5 = 1 \\ g'(0{,}5) &= -2\cdot 0{,}5 + 2 = 1 \end{align*} Leikkauspisteeseen asetettujen tangenttien kulmakertoimet ovat siis samat, joten kysymyksessä on yksi yhteinen tangetti.
Käyrän tangentti
Osoita, että paraabelit $$y = ax^2 + 2x$$ ja $$ y = ax^2 - \frac{1}{2}x $$ leikkaavat toisensa kohtisuorasti origossa riippumatta kertoimen $a$ arvosta.
Vastaus
Kumpikin paraabeli kulkee pisteen $(0,0)$, joten ne leikkaavat toisensa origossa. Vastaavien polynomifunktioiden derivaattafunktioiden arvot origossa ovat \begin{align*} f'(0) &= 2a \cdot 0 + 2 = 2 \\[2mm] g'(0) &= 2a \cdot 0 - \frac{1}{2} = -\frac{1}{2} \end{align*} Koska paraabeleille origoon asetettujen tangenttien kulmakertoimien tulo on $-1$, ne ovat kohtisuorassa toisiaan vastaan (ks. MAA5-kurssin teoreema 11).
Käyrän tangentti
Onko mahdollista valita vakiolle $a$ sellainen arvo, että käyrän $y = x^3$ pisteeseen $(1,1)$ asetettu tangentti sivuaa myös käyrää $y = a - x^2$?
Vastaus
Kyllä, $a = -\frac{17}{4}$.
Ohjeita:
- Muodosta käyrän $y = x^3$ pisteeseen $(1,1)$ asetetun tangentin yhtälö.
- Määritä käyrän $y = a-x^2$ tangentin kulmakerroin.
- Selvitä, missä kohdassa tangenteilla on sama kulmakerroin.
- Selvitä sivuamispisteen $y$-koordinaatti ja ratkaise sen avulla $a$.
Derivaatan määritelmä
Tarkastellaan funktiota $f(x) = 4x - x^2$. Tehtävänä on määrittää $f'(1)$ derivaatan määritelmään nojautuen.
- Muodosta funktion $f$ erotusosamäärä kohdassa $1$.
- Jaa erotusosamäärän osoittaja tekijöihin MAA2-kurssin teoreeman 8 avulla.
- Mitä on $f'(1)$?
Vastaus
- $\dfrac{-x^2+4x-3}{x-1}$
- $-x^2+4x-3 = -(x-1)(x-3)$
- $f'(1) = 2$
Derivaatan määritelmä
Tehtävänä on johtaa funktion $$ f(x) = \frac{x-1}{x+1} $$ derivaattafunktion lauseke derivaatan määritelmän avulla.
- Muodosta funktion $f$ erotusosamäärä kohdassa $a$.
- Lavenna erotusosamäärän osoittajassa esiintyvät murtolausekkeet samannimisiksi ja sievennä niiden erotus mahdollisimman pitkälle.
- Tee kaikki mahdolliset supistukset.
- Mitä on $f'(a)$?
Vastaus
- $\dfrac{\frac{x-1}{x+1} - \frac{a-1}{a+1}}{x-a}$
- $\dfrac{\frac{2(x-a)}{(x+1)(a+1)}}{x-a}$
- $\dfrac{2}{(x+1)(a+1)}$
- $f'(a) = \dfrac{2}{(a+1)^2}$
TEHTÄVÄSARJA III
Määritä paraabelin $y = 2x^2 + bx + 3$ huippu ja totea, että se kertoimen $b$ arvosta riippumatta sijaitsee paraabelilla $y = −2x^2 + 3$.
[Pitkä K2005/5]
Vastaus
Huipun $x$-koordinaatti on derivaatan nollakohta $-\frac{1}{4}b$. Sen avulla saadaan laskettua $y$-koordinaatti $-\frac{1}{8}b^2 + 3$. Nämä toteuttavat paraabelin $y = −2x^2 + 3$ yhtälön riippumatta kertoimen $b$ arvosta.
Määritä käyrän $y = x^3$ pisteeseen $(2,8)$ piirretyn tangentin yhtälö. Missä pisteessä tangentti leikkaa $y$-akselin? Määritä tangentin, $y$-akselin ja suoran $y = 8$ määräämän kolmion pinta-ala.
[Pitkä K2001/2]
Vastaus
Tangentin yhtälö on $y = 12x - 16$. Tangentti leikkaa $y$-akselin pisteessä $(0,-16)$. Kolmion pinta-ala on $24$.
Osoita erotusosamäärää tutkimalla, että funktio $$ f(x) = \frac{x}{1 + \left|x\right|} $$ on derivoituva kohdassa $x = 0$.
[Pitkä K2015/13a]
Vastaus
\begin{align*} \frac{f(x) - f(0)}{x-0} = \frac{1}{1 + \left|x\right|} \xrightarrow[x\rightarrow 0]{} 1 \end{align*}
- Millä muuttujan $x$ arvoilla polynomin $P(x) = x^4 - x^3 + x$ derivaatta saa arvon $1$?
- Määritellään funktiot $f(x) = x^3 - 3x$ ja $g(x) = \frac{1}{2}f(2x)$, kun $x \in \R$. Laske derivaatta $g'(1)$.
Vinkki: aloita sieventemällä funktion $g$ lauseke.
Vastaus
- Muuttujan arvoilla $x = 0$ ja $x = \frac{3}{4}$
- $g'(1) = 9$
Millä parametrin $k$ arvoilla käyrien $y = kx^2$ ja $y = k(x-2)^2$ leikkauspisteeseen piirretyt tangentit ovat kohtisuorassa toisiaan vastaan?
[Pitkä S2013/4]Vastaus
Parametrin arvoilla $k = \pm\frac{1}{2}$.
- Määritä sellainen kerroin $a$, että funktio $$ f(x) = \begin{cases} ax^2, &\text{ jos $x \leq -1$,} \\[2mm] \dfrac{x^2}{1+x^2}, &\text{ jos $x > -1$.} \end{cases} $$ on jatkuva kaikkialla.
- Onko funktio $f(x)$ tällöin derivoituva kaikkialla?
[Pitkä K2011/11a&b]
Vinkki: b-kohdassa tutki erotusosamäärän raja-arvoa kahdessa tapauksessa: jos $x \rightarrow (-1)-$ ja jos $x \rightarrow (-1)+$.
Vastaus
- $a = \frac{1}{2}$
- Funktio ei ole derivoituva kohdassa $x = -1$, sillä erotusosamäärän vasemman- ja oikeanpuoleinen raja-arvo ovat tässä kohdassa erisuuruiset. Vasemmanpuoleinen raja-arvo on $-1$ ja oikeanpuoleinen on $-\frac{1}{2}$.
Neljännen asteen polynomilla $3x^4 - 8x^3 - 18x^2 + 7$ ja sen derivaatalla on yhteinen nollakohta. Määritä tämä yhteinen nollakohta.
[Pitkä K2009/4]
Vastaus
$x = -1$
Tiedetään, että funktio $f$ kasvaa varsin tarkoin lineaarisesti (suoraviivaisesti) välillä $[1{,}9995; 2{,}0005]$. Lisäksi tiedetään funktion arvot $f(2) = 3{,}7458053$ ja $f(2{,}0005) = 3{,}7458664$. Määritä tämän perusteella likiarvo derivaatalle $f'(2)$.
[Pitkä K2006/12]
Vastaus
$f'(x) \approx 0{,}1222$.
Olkoon funktio $f$ jatkuva origossa. Määritä erotusosamäärän avulla funktion $g(x) = xf(x)$ derivaatta origossa. Voidaanko tulosta soveltaa funktioon $f(x) = \left|x\right| + 1$?
[Pitkä K2005/12]
Vastaus
\begin{align*} \frac{g(x) - g(0)}{x-0} &= \frac{xf(x) - 0\cdotf(0)}{x} \\[2mm] &= \frac{xf(x)}{x} \\[2mm] &= f(x) \xrightarrow[x \rightarrow 0]{} f(0) \end{align*} Tulosta voidaan soveltaa funktioon $f(x) = \left|x\right| + 1$, sillä se on jatkuva origossa. Funktiolla $g(x) = x\left|x\right| + x$ on siis origossa derivaatta $g'(0) = f(0) = 1$.
Määritä funktion $$ f(x) = \frac{1}{x} $$ derivaatta kohdassa $x = 2$ laskemalla erotusosamäärän raja-arvo.
[Pitkä S2004/10]
Vastaus
\begin{align*} \frac{f(x) - f(2)}{x-2} &= \frac{\frac{1}{x} - \frac{1}{2}}{x-2} \\[2mm] &= \frac{\frac{2-x}{2x}}{x-2} \\[2mm] &= \frac{-(x-2)}{2x} \cdot \frac{1}{x-2} \\[2mm] &= \frac{-1}{2x} \xrightarrow[x \rightarrow 2]{} -\frac{1}{4} \end{align*} Siis $f'(2) = -\frac{1}{4}$.
Määritä se paraabelin $y = x^2-2x-3$ piste, jossa paraabelin tangentin suuntakulma on $+45^\circ$.
[Pitkä K2004/5]
Vastaus
Piste on $\left(\frac{3}{2}, -\frac{15}{4}\right)$.
Olkoon $f(x) = x^2 - 3x - 5$.
- Ratkaise yhtälö $f(x) = 0$.
- Millä muuttujan $x$ arvoilla on $f'(x) = 1$?
- Piirrä derivaattafunktion $f'$ kuvaaja.
[Pitkä S2003/1]
Vastaus
- $x = \frac{1}{2}(3 \pm \sqrt{29})$
- $x = 2$
- Kuvaaja on suora, jonka yhtälö on $y = 2x -3$. Se kulkee siis pisteiden $(0,-3)$ ja $(1,-1)$ kautta.
Osoita, että käyrillä $x^2 -6x - 3 + 4y = 0$ ja $2x^2 + 1 - y = 0$ on yksi yhteinen piste, jossa ne sivuavat toisiaan, so. niillä on yhteinen tangetti. Määritä tämän tangentin yhtälö.
[Pitkä S2001/4]
Vastaus
Käyrillä on yksi yhteinen piste: $\left(\frac{1}{3}, \frac{11}{9}\right)$. Käyriä vastaavien polynomifunktioiden derivaatat saavat saman arvo kohdassa $x = \frac{1}{3}$, joten niillä on tässä yhteisessä pisteessä yhteinen tangentti. Tangetin yhtälö on $12x - 9y + 7 = 0$.
Paraabelin $y = ax^2 + bx − 3$ huippu on pisteessä $\left(\frac{3}{2}, 1\right)$. Määritä kertoimet $a$ ja $b$.
[Lyhyt K2007/12]
Vastaus
$a = -\frac{16}{9}$ ja $b = \frac{16}{3}$
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

