Trigonometriset funktiot
Luvun tavoitteet
Tämän luvun tavoitteena on, että tunnet trigonometristen funktioiden kuvaajat ja perusominaisuudet ja ymmärrät niiden yhteyden yksikköympyrään. Osaat
- käyttää radiaania kulman yksikkönä
- hahmotella sini-, kosini- ja tangenttifunktioiden kuvaajat kynän ja paperin avulla
- päätellä, miten erilaiset kertoimet ja vakiot vaikuttavat sini- ja kosinifunktioiden kuvaajien muotoon
- ratkaista trigonometrisia yhtälöitä sekä yksikköympyrän avulla että graafisesti koordinaatistossa
- muodostaa trigonometristen funktioiden derivaattafunktiot
- tutkia trigonometristen funktioiden kulkua soveltamalla MAA6-kurssissa oppimiasi asioita.
Radiaani kulman yksikkönä
Edellisessä luvussa määriteltiin kulman $\alpha$ sini ja kosini yksikköympyrän avulla. Jokaista suunnattua kulmaa vastaa täsmälleen yksi sinin ja kosinin arvo, joten siniä ja kosinia voidaan ajatella myös funktioina. Jotta näiden funktioiden kuvaajat voidaan piirtää tavalliseen koordinaatistoon, pitää niiden määrittely- eli lähtöjoukkona olla reaalilukujen joukko. Tämä tarkoittaa, että kulman suuruus pitää ilmaista asteiden sijaan pelkkänä reaalilukuna. Tätä varten määritellään uusi kulman yksikkö, radiaani.
MÄÄRITELMÄ: RADIAANI
Kulman suuruus radiaaneina on kulmaa vastaavan ympyrän kaaren pituuden suhde ympyrän säteeseen: $$ \alpha = \frac{b}{r} $$ 
Jos kulma mitataan radiaanin määritelmän mukaisesti, tuloksena todella on pelkkä reaaliluku.
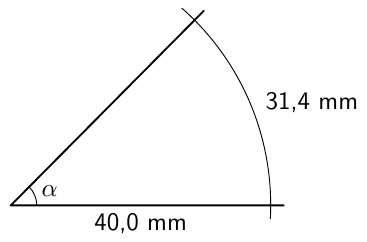
Esimerkiksi yllä olevassa kuvassa mittauksessa käytetyn ympyrän säde on 40,0 mm ja kulmaa vastaavan kaaren pituus on 31,4 mm, jolloin kulmaksi $\alpha$ saadaan $$ \alpha = \frac{31{,}4 \text{ mm}}{40{,}0 \text{ mm}} = 0{,}785. $$ Pituuden yksiköt supistuvat pois ja tulos on paljas luku. Jos halutaan korostaa, että yksikkönä on asteen sijaan radiaani, voidaan merkitä myös $\alpha = 0{,}785 \text{ rad}$. Yleensä kuitenkin merkitään lyhyesti $\alpha = 0{,}785$.
Kulman suuruus radiaaneina
Tässä tehtävässä määritetään oikokulman $180^\circ$ suuruus radiaaneina.
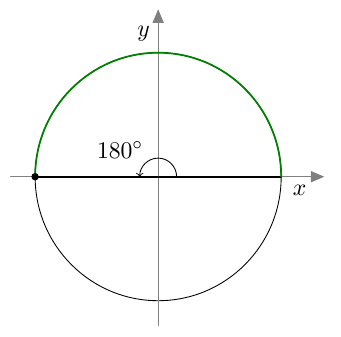
- Mikä on yksikköympyrän säteen pituus? Entä yksikköympyrän kehän pituus?
Vinkki: kertaa tarvittaessa MAA3-kurssin teoreema 13. - Päättele a-kohdan avulla, mikä on oikokulmaa vastaavan yksikköympyrän kaaren pituus.
- Mikä on oikokulman suuruus radiaaneina?
VASTAUS
- Yksikköympyrän säteen pituus on $r = 1$ ja kehän pituus on $p = 2\pi r = 2\pi$.
- Oikokulmaa vastaavan kaaren pituus on puolet koko yksikköympyrän kehästä eli $\pi$.
- Oikokulman suuruus on $\dfrac{\pi}{1}$ eli $\pi$ (radiaania).
Edellisen tehtävän tuloksesta saadaan seuraava teoreema:
TEOREEMA
Oikokulma $180^\circ$ on $\pi$ radiaania.
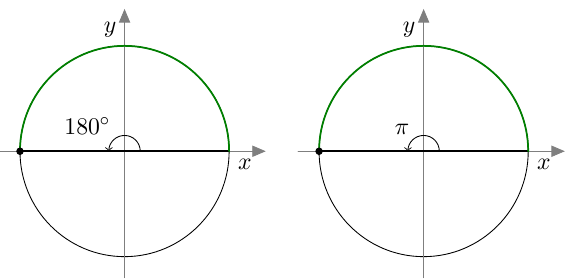
Perustelu tehtävässä 2.1.
Monien muiden kulmien suuruus radiaaneina saadaan pääteltyä miettimällä, miten suuri osa oikokulmasta on kysymyksessä. Esimerkiksi kulma $135^\circ$ on kolme neljäsosaa oikokulmasta, joten sen suuruus radiaaneina on $\frac{3}{4}\pi$. 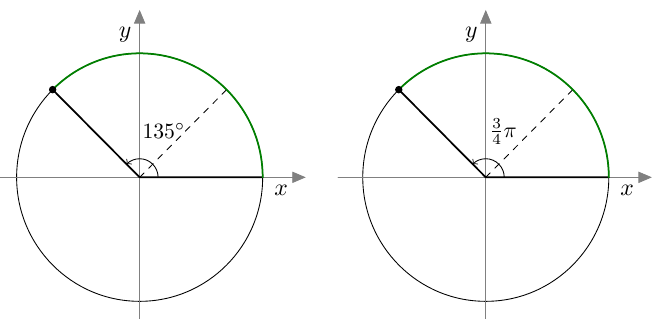
Kulman suuruus radiaaneina
Piirrä yksikköympyrä, merkitse siihen seuraavat kulmat ja päättele niiden suuruus radiaaneina. Käytä apuna teoreemaa 12.
- $30^\circ$
- $60^\circ$
- $90^\circ$
- $120^\circ$
- $150^\circ$
- $180^\circ$
- $210^\circ$
- $240^\circ$
- $270^\circ$
- $300^\circ$
- $330^\circ$
- $360^\circ$
Vinkki: minkä kulman monikertoja kaikki yllä mainitut kulmat ovat?
VASTAUS
Kaikki kulmat ovat kulman $30^\circ$ monikertoja.
- $\frac{1}{6}\pi$
- $\frac{1}{3}\pi$
- $\frac{1}{2}\pi$
- $\frac{2}{3}\pi$
- $\frac{5}{6}\pi$
- $\pi$
- $\frac{7}{6}\pi$
- $\frac{4}{3}\pi$
- $\frac{3}{2}\pi$
- $\frac{5}{3}\pi$
- $\frac{11}{6}\pi$
- $2\pi$
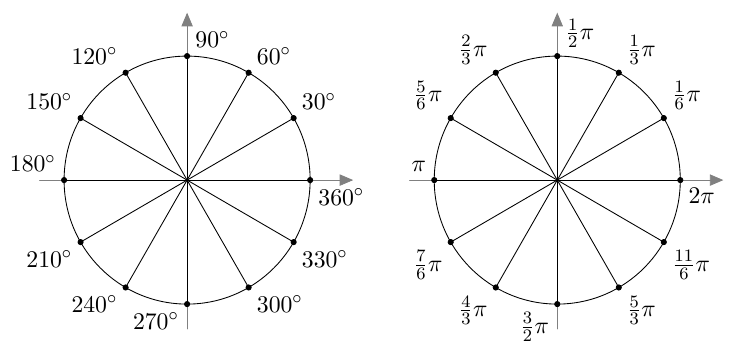
Kulman suuruus radiaaneina
Piirrä yksikköympyrä, merkitse siihen seuraavat kulmat ja päättele niiden suuruus asteina. Käytä apuna teoreemaa 12.
- $\frac{1}{4}\pi$
- $\frac{1}{2}\pi$
- $\frac{3}{4}\pi$
- $\pi$
- $\frac{5}{4}\pi$
- $\frac{3}{2}\pi$
- $\frac{7}{4}\pi$
- $2\pi$
Vinkki: minkä kulman monikertoja kaikki yllä mainitut kulmat ovat?
VASTAUS
Kaikki kulman ovat kulman $\frac{1}{4}\pi$ monikertoja.
- $45^\circ$
- $90^\circ$
- $135^\circ$
- $180^\circ$
- $225^\circ$
- $270^\circ$
- $315^\circ$
- $360^\circ$
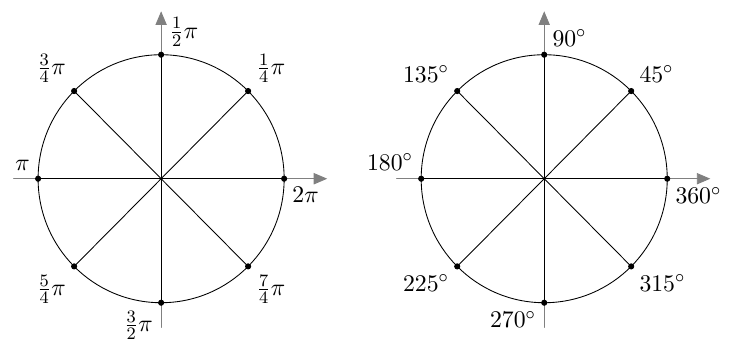
Kulman yksikkö voidaan vaihtaa asteista radiaaneiksi tai päinvastoin myös verrannon avulla. Seuraavassa selvitetään esimerkin vuoksi, kuinka monta astetta on 1 radiaani.
Tiedetään, että $180^\circ$ vastaa $\pi$ radiaania. Voidaan muodostaa verranto $$ \frac{x}{1} = \frac{180^\circ}{\pi}, \qquad \left(\frac{\text{asteet}}{\text{radiaanit}}\right) $$ jossa $x$ on 1 radiaanin kulma asteina. Saadaan $$ x = \frac{180^\circ}{\pi} \approx 57{,}3^\circ. $$ Yhden radiaanin kulma on siis noin 57,3 astetta. Sitä vastaava ympyrän kaari on yhtä pitkä kuin ympyrän säde, joten yksikköympyrässä yhden radiaanin kulma näyttää tältä: 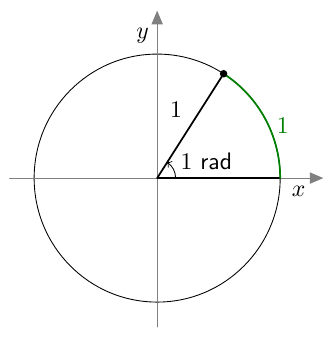
Kulman suuruus radiaaneina
Muuta seuraavat kulma asteista radiaaneksi tai päinvastoin verrannon avulla.
- $15^\circ$
- $1^\circ$
- $\dfrac{1}{5}\pi$
- $\dfrac{7}{10}\pi$
VASTAUS
- $\dfrac{1}{12}\pi \approx 0{,}262$
- $\dfrac{1}{180}\pi \approx 0{,}017$
- $36^\circ$
- $126^\circ$
Palataan vielä hetkeksi pohtimaan edellä esitettyä radiaanin määritelmää. Riippuuko sen antama kulman suuruus siitä, miten mittauksessa käytetty ympyrä valitaan? Jos ympyrän sädettä kasvatetaan, antaako määritelmä kuitenkin kulmalle saman arvon?
MAA3-kurssin teoreemassa 14 osoitettiin, että ympyrän kaaren pituus $b$ riippuu keskuskulmasta $\alpha$ ja ympyrän säteestä $r$: $$ b = \frac{\alpha}{360^\circ} \cdot 2\pi r. $$ Radiaanin määritelmässä esiintyvä osamäärä ei siis riipu ympyrän säteestä: \begin{align*} \frac{b}{r} &= \frac{\alpha}{360^\circ} \cdot \frac{2\pi r}{r} \\[2mm] &= \frac{\alpha}{360^\circ} \cdot 2\pi. \end{align*} Havaitaan, että kulman $\alpha$ suuruus radiaaneina saadaan myös vertaamalla kulmaa $\alpha$ täyskulmaan ja ottamalla vastaava osuus luvusta $2\pi$.
Sinifunktio
Sinifunktion kuvaaja saadaan muodostettua yksikköympyrän avulla, kun kulma ilmaistaan radiaaneina. Kuvaajaa hahmotellaan seuraavissa tehtävissä.
Sinifunktion kuvaaja
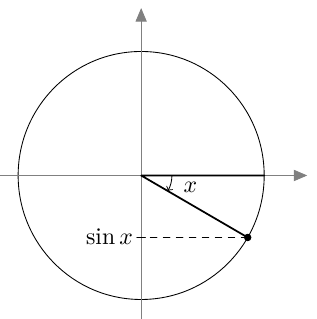
Päättele yksikköympyrän avulla, mitä on $\sin x$, jos kulma on radiaaneissa ilmaistuna
- $x = -\frac{1}{2}\pi$
- $x = 0$
- $x = \frac{1}{2}\pi$
- $x = \pi$
- $x = \frac{3}{2}\pi$
- $x = 2\pi$
Hahmottele sinifunktion kuvaajaa merkitsemällä pisteet $(x, \sin x)$ koordinaatistoon.
VASTAUS
- $\sin\left(-\frac{1}{2}\pi \right) = -1$
- $\sin 0 = 0$
- $\sin\left(\frac{1}{2}\pi \right) = 1$
- $\sin \pi = 0$
- $\sin\left(\frac{3}{2}\pi \right) = -1$
- $\sin 2\pi = 0$
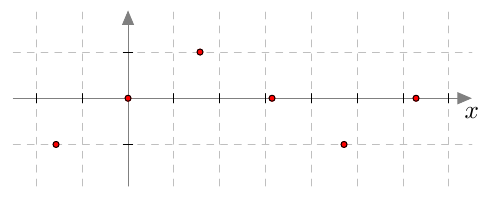
Edellisen tehtävän yksittäiset pisteet eivät anna vielä kunnollista käsitystä sinifunktion kuvaajasta. Kun kuvaajan pisteitä lasketaan huomattavasti enemmän, muodostuu niistä vähitellen yhtenäinen kuvaaja. Tätä havainnollistetaan seuraavassa tehtävässä.
Sinifunktion kuvaaja
Tutki sinifunktion kuvaajaa tämän Geogebra-havainnollistuksen avulla. Päättele vastaukset seuraaviin kysymyksiin:
- Miten kulma $\alpha$ näkyy yksikköympyrässä? Entä sinifunktion kuvaajassa?
- Miten sinin arvo $\sin\alpha$ näkyy yksikköympyrässä? Entä sinifunktion kuvaajassa?
- Missä $x$-akselin kohdissa sinifunktio saa arvon nolla?
- Mikä on sinifunktion suurin arvo? Missä $x$-akselin kohdissa se saavutetaan?
- Mikä on sinifunktion pienin arvo? Missä $x$-akselin kohdissa se saavutetaan?
- Miten kuvaajasta näkyy, että sinifunktio on jaksollinen funktio, jonka jakso on $2\pi$?
VASTAUS
- Kulma $\alpha$ näkyy yksikköympyrässä suunnattuna kulmana ja sinifunktion kuvaajassa kuvaajan pisteen $x$-koordinaattina.
- Sinin arvo $\sin\alpha$ on yksikköympyrän kehäpisteen $y$-koordinaatti ja sinifunktion kuvaajan pisteen $y$-koordinaatti.
- Kohdissa $x = n\pi$, missä $n$ on kokonaisluku.
- Sinifunktion suurin arvo on $1$ ja se saavutetaan kohdissa $x = \frac{\pi}{2} + n\cdot 2\pi$, missä $n$ on kokonaisluku.
- Sinifunktion pienin arvo on $-1$ ja se saavutetaan kohdissa $x = -\frac{\pi}{2} + n\cdot 2\pi$, missä $n$ on kokonaisluku.
- Sinifunktion arvot toistuvat aina $2\pi$ välein eli $\sin (x + 2\pi) = \sin x$ kaikilla kulmilla $x$.
Kootaan edellisen tehtävän havainnot vielä teoreemaksi. Perustelussa voidaan nojautua yksikköympyrään.
TEOREEMA
Sinifunktion arvojoukko on suljettu väli $[-1,1]$.
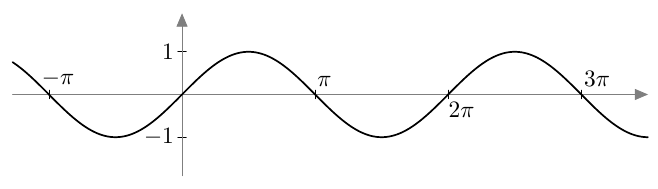
Sinifunktio on jaksollinen funktio. Sen jakso on $2\pi$ eli kaikilla muuttujan $x$ arvoilla pätee $$ \sin(x + 2\pi) = \sin x. $$
Perustelu:
- Yksikköympyrästä nähdään, että sinin suurin mahdollinen arvo on $1$, pienin mahdollinen arvo $-1$ ja sini saa kaikki arvot väliltä $[-1,1]$. Asiaa on käsitelty tarkemmin tehtävässä 1.4.
- Kulmilla $x$ ja $x + 2\pi$ on yksikköympyrässä sama kehäpiste, joten $\sin(x + 2\pi) = \sin x$.

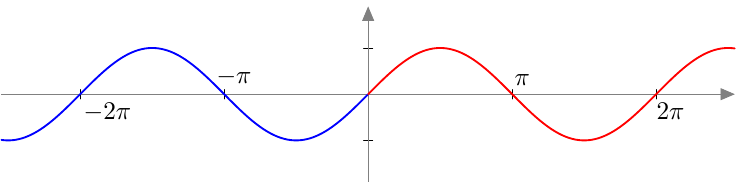
Sinifunktio saa kaikki arvonsa millä tahansa välillä, jonka pituus on jakson pituus $2\pi$. Alla on näkyvissä joitakin esimerkkejä, joissa sinifunktion yksi jakso on merkitty punaisella: 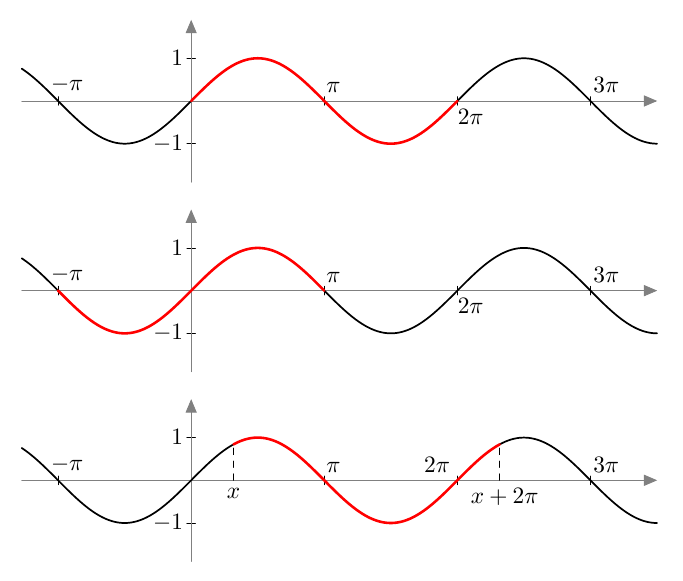
Sinifunktion kuvaaja
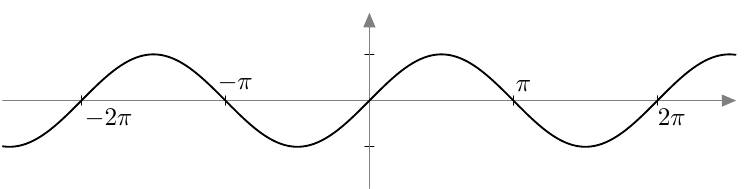
Päättele yllä näkyvän sinifunktion kuvaajan avulla vastaukset seuraaviin kysymyksiin:
- Teoreeman 2 mukaan kulman ja sen vastakulman sinit ovat toistensa vastalukuja eli $$\sin(-x) = -\sin x$$ kaikilla kulmilla $x$. Miten tämä näkyy sinifunktion kuvaajassa? Selitä omin sanoin.
- Onko sinifunktio jatkuva?
- Onko sinifunktio derivoituva?
Vinkki: Kertaa tarvittaessa b- ja c-kohdissa MAA6-kurssin luku 2.
VASTAUS
- Kuvaaja on symmetrinen origon suhteen:
- Sinifunktion kuvaaja on katkematon käyrä, joten sinifunktio näyttäisi olevan jatkuva.
- Sinifunktion kuvaajan jokaiseen pisteeseen voidaan asettaa tangentti tasan yhdellä tavalla, joten sinifunktio näyttäisi olevan derivoituva.
Seuraavissa tehtävissä tutkitaan, miten erilaisilla kertoimilla voidaan vaikuttaa sinifunktion kuvaajan muotoon.
Kertoimien vaikutus sinifunktioon
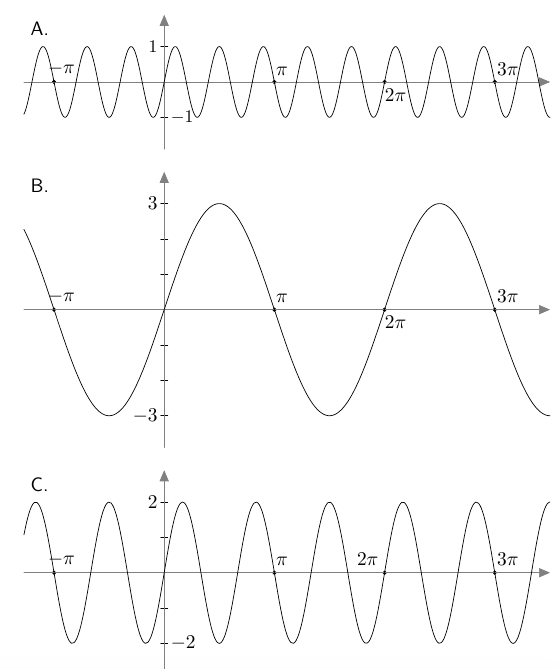
Yhdistä funktio ja sen kuvaaja. Vastaa sen jälkeen tehtävän lopussa oleviin kysymyksiin.
- $f(x) = 3 \sin x$
- $g(x) = 2 \sin 3x$
- $h(x) = \sin 5x$
- Mikä on funktion $f(x) = 3 \sin x$ suurin arvo? Entä pienin? Mikä on funktion $f$ jakso?
- Mikä on funktion $g(x) = 2 \sin 3x$ suurin arvo? Entä pienin? Kuinka monta funktion $g$ jaksoa mahtuu $2\pi$ mittaisen välin sisään? Mikä on funktion $g$ jakso?
- Kuinka monta funktion $h(x) = \sin 5x$ jaksoa mahtuu $2\pi$ mittaisen välin sisään? Mikä on funktion $h$ jakso?
VASTAUS
Funktion $f$ kuvaaja on B.
Funktion $g$ kuvaaja on C.
Funktion $h$ kuvaaja on A.
- Funktion $f(x) = 3 \sin x$ suurin arvo on $3$ ja pienin $-3$. Sen jakso on $2\pi$.
- Funktion $g(x) = 2 \sin 3x$ suurin arvo on $2$ ja pienin $-2$. Kolme sen jaksoa mahtuu $2\pi$ mittaisen välin sisään, joten yhden jakson pituus on $\frac{2\pi}{3}$.
- Funktion $h(x) = \sin 5x$ suurin arvo on $1$ ja pienin $-1$. Viisi sen jaksoa mahtuu $2\pi$ mittaisen välin sisään, joten yhden jakson pituus on $\frac{2\pi}{5}$.
Kertoimien vaikutus sinifunktioon
Tutki edellisen tehtävän tuloksia ja päättele vastaukset seuraaviin kysymyksiin:
- Miten kerroin $k$ vaikuttaa funktion $f(x) = k\sin x$ kuvaajan muotoon? Voit tutkia asiaa myös tämän Geogebra-havainnollistuksen avulla.
- Miten kerroin $k$ vaikuttaa funktion $g(x) = \sin kx$ kuvaajan muotoon? Voit tutkia asiaa myös tämän Geogebra-havainnollistuksen avulla.
Tutkitaan vielä lopuksi, miten siniyhtälöiden ratkaisuja voidaan havainnollistaa koordinaatistossa.
Siniyhtälö
Tehtävänä on ratkaista yhtälö $$ 3\sin x = 1. $$
- Alla ovat näkyvissä funktioiden $f(x) = 3\sin x$ ja $g(x) = 1$ kuvaajat. Miten yhtälön $3\sin x = 1$ ratkaisut näkyvät kuvassa?
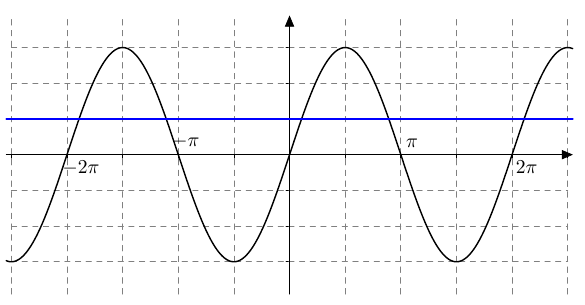
- Ratkaise yhtälö $$ 3\sin x = 1 $$ yksikköympyrän avulla samalla tekniikalla kuin luvussa 1, mutta käytä kulman yksikkönä asteen sijaan radiaania. Anna vastaukset kolmen merkitsevän numeron tarkkuudella.
Vinkki: kertaa tarvittaessa tehtävä 1.9.
VASTAUS
- Yhtälön ratkaisuja ovat ne kohdat, joissa funktiot saavat saman arvon eli niiden kuvaajat leikkaavat:
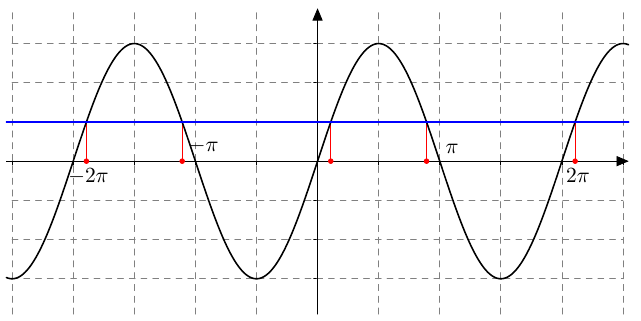
- $x \approx 0{,}340 + n \cdot 2\pi$ tai $x \approx 2{,}80 + n \cdot 2\pi$, missä $n$ on kokonaisluku.
Siniyhtälö
Tutkitaan yhtälön $\sin x = 0{,}5x$ ratkaisuja.
- Mikä on funktion $f(x) = \sin x$ suurin arvo? Entä pienin? Pystytkö näiden tietojen avulla rajaamaan $x$-akselin välin, jolla yhtälön $\sin x = 0{,}5x$ ratkaisujen täytyy olla?
- Piirrä funktioiden $f(x) = \sin x$ ja $g(x) = 0{,}5x$ kuvaajat samaan koordinaatistoon ja määritä yhtälön $\sin x = 0{,}5x$ ratkaisujen likiarvot graafisesti.
VASTAUS
- Koska $-1 \leq \sin x \leq 1$ kaikilla kulmilla $x$, yhtälön ratkaisut toteuttavat epäyhtälön $$ -1 \leq 0{,}5x \leq 1 $$ eli $$ -2 \leq x \leq 2. $$
- Ratkaisut ovat $x \approx \pm 1{,}9$ ja $x = 0$:
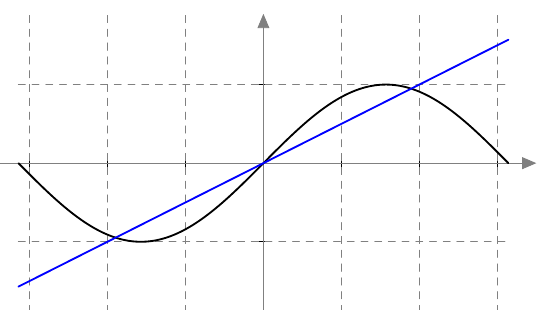
Kosinifunktio
Kosinifunktion kuvaaja saadaan muodostettua yksikköympyrän avulla samaan tapaan kuin edellisessä luvussa. Kuvaajaa hahmotellaan seuraavissa tehtävissä.
Kosinifunktion kuvaaja
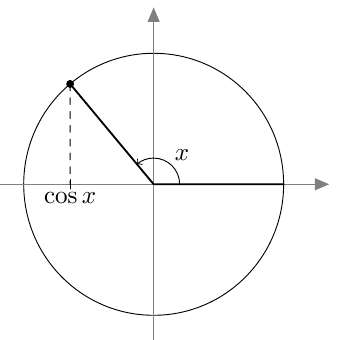
Päättele yksikköympyrän avulla, mitä on $\cos x$, jos kulma on radiaaneissa ilmaistuna
- $x = -\frac{1}{2}\pi$
- $x = 0$
- $x = \frac{1}{2}\pi$
- $x = \pi$
- $x = \frac{3}{2}\pi$
- $x = 2\pi$
Hahmottele kosinifunktion kuvaajaa merkitsemällä pisteet $(x, \cos x)$ koordinaatistoon.
VASTAUS
- $\cos\left(-\frac{1}{2}\pi \right) = 0$
- $\cos 0 = 1$
- $\cos\left(\frac{1}{2}\pi \right) = 0$
- $\cos \pi = -1$
- $\cos\left(\frac{3}{2}\pi \right) = 0$
- $\cos 2\pi = 1$
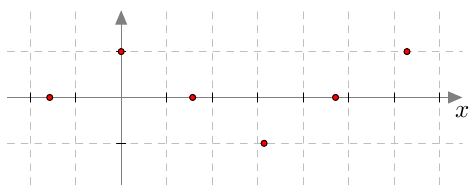
Yksittäiset pisteet eivät anna vielä kunnollista käsitystä kosinifunktion kuvaajasta. Kun kuvaajan pisteitä lasketaan huomattavasti enemmän, muodostuu niistä vähitellen yhtenäinen käyrä. Tätä havainnollistetaan seuraavassa tehtävässä.
Kosinifunktion kuvaaja
Tutki kosinifunktion kuvaajaa tämän Geogebra-havainnollistuksen avulla. Päättele vastaukset seuraaviin kysymyksiin:
- Miten kulma $\alpha$ näkyy yksikköympyrässä? Entä kosinifunktion kuvaajassa?
- Miten kosinin arvo $\cos\alpha$ näkyy yksikköympyrässä? Entä kosinifunktion kuvaajassa?
- Missä $x$-akselin kohdissa kosinifunktio saa arvon nolla?
- Mikä on kosinifunktion suurin arvo? Missä $x$-akselin kohdissa se saavutetaan?
- Mikä on kosinifunktion pienin arvo? Missä $x$-akselin kohdissa se saavutetaan?
- Miten kuvaajasta näkyy, että kosinifunktio on jaksollinen funktio, jonka jakso on $2\pi$?
VASTAUS
- Kulma $\alpha$ näkyy yksikköympyrässä suunnattuna kulmana ja kosinifunktion kuvaajassa kuvaajan pisteen $x$-koordinaattina.
- Kosinin arvo $\cos\alpha$ on yksikköympyrän kehäpisteen $x$-koordinaatti ja kosinifunktion kuvaajan pisteen $y$-koordinaatti.
- Kohdissa $x = \frac{\pi}{2} + n\pi$, missä $n$ on kokonaisluku.
- Kosinifunktion suurin arvo on $1$ ja se saavutetaan kohdissa $x = n\cdot 2\pi$, missä $n$ on kokonaisluku.
- Kosinifunktion pienin arvo on $-1$ ja se saavutetaan kohdissa $x = \pi + n\cdot 2\pi$, missä $n$ on kokonaisluku.
- Kosinifunktion arvot toistuvat aina $2\pi$ välein eli $\cos (x + 2\pi) = \cos x$ kaikilla kulmilla $x$.
Kootaan edellisen tehtävän havainnot teoreemaksi. Perustelussa voidaan nojautua yksikköympyrään.
TEOREEMA
Kosinifunktion arvojoukko on suljettu väli $[-1,1]$.
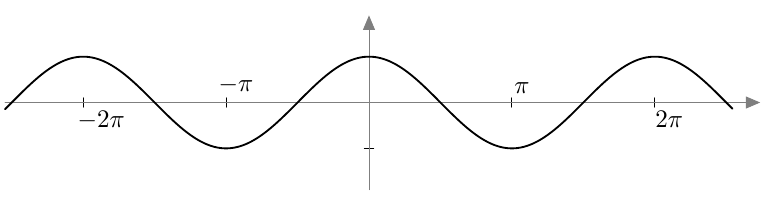
Kosinifunktio on jaksollinen funktio. Sen jakso on $2\pi$ eli kaikilla muuttujan $x$ arvoilla pätee $$ \cos(x + 2\pi) = \cos x. $$
Perustelu:
- Yksikköympyrästä nähdään, että kosinin suurin mahdollinen arvo on $1$, pienin mahdollinen arvo $-1$ ja kosini saa kaikki arvot väliltä $[-1,1]$. Asiaa on käsitelty tarkemmin tehtävässä 1.15.
- Kulmilla $x$ ja $x + 2\pi$ on yksikköympyrässä sama kehäpiste, joten $\cos(x + 2\pi) = \cos x$.
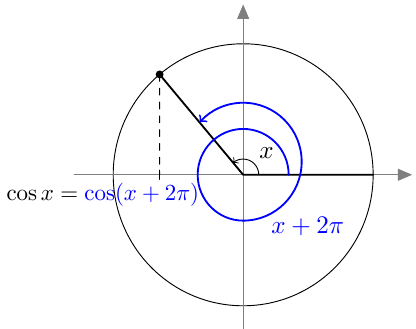
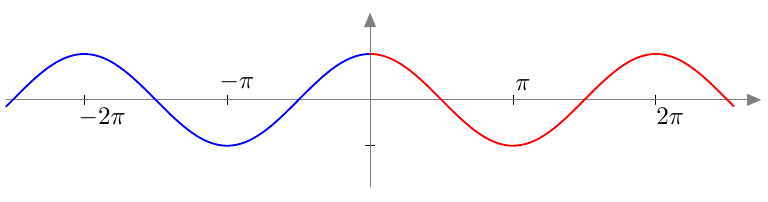
Kosinifunktio saa kaikki arvonsa millä tahansa välillä, jonka pituus on jakson pituus $2\pi$. Alla on näkyvissä joitakin esimerkkejä, joissa kosinifunktion yksi jakso on merkitty punaisella: 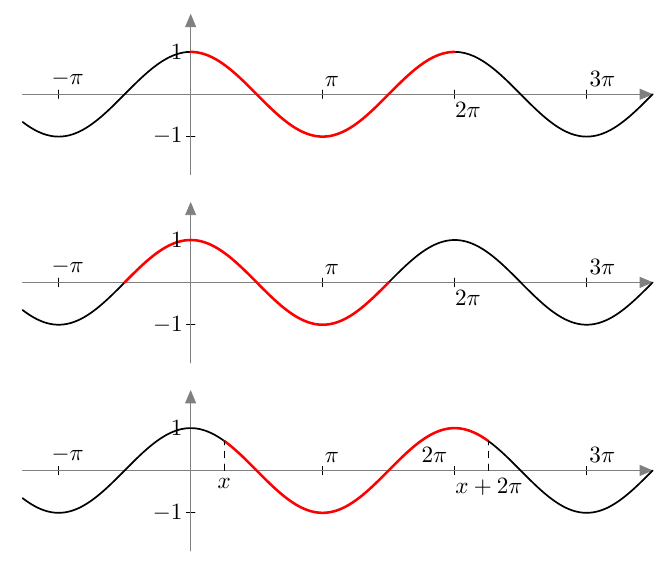
Kosinifunktion kuvaaja

Päättele yllä näkyvän kosinifunktion kuvaajan avulla vastaukset seuraaviin kysymyksiin:
- Teoreeman 5 mukaan kulman ja sen vastakulman kosinit ovat samat eli $$\cos(-x) = \cos x$$ kaikilla kulmilla $x$. Miten tämä näkyy kosinifunktion kuvaajassa? Selitä omin sanoin.
- Onko kosinifunktio jatkuva?
- Onko kosinifunktio derivoituva?
Vinkki: Kertaa tarvittaessa b- ja c-kohdissa MAA6-kurssin luku 2.
VASTAUS
- Kuvaaja on symmetrinen $y$-akselin suhteen:
- Kosinifunktion kuvaaja on katkematon käyrä, joten kosinifunktio näyttäisi olevan jatkuva.
- Kosinifunktion kuvaajan jokaiseen pisteeseen voidaan asettaa tangentti tasan yhdellä tavalla, joten kosinifunktio näyttäisi olevan derivoituva.
Kertoimien vaikutus kosinifunktioon
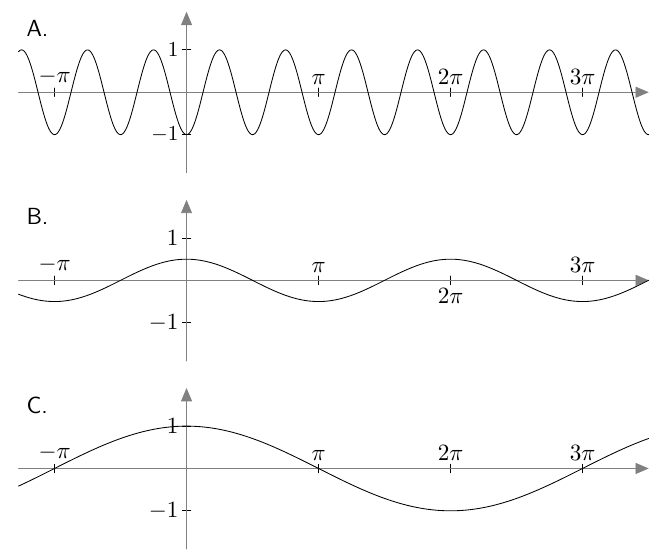
Yhdistä funktio ja sen kuvaaja. Vastaa sen jälkeen tehtävän lopussa oleviin kysymyksiin.
- $f(x) = \cos \dfrac{x}{2}$
- $g(x) = -\cos 4x$
- $h(x) = 0{,}5\cos x$
- Mikä on funktion $h(x) = 0{,}5\cos x$ suurin arvo? Entä pienin? Mikä on funktion $h$ jakso?
- Mikä on funktion $g(x) = -\cos 4x$ suurin arvo? Entä pienin? Kuinka monta funktion $g$ jaksoa mahtuu $2\pi$ mittaisen välin sisään? Mikä on funktion $g$ jakso?
- Mikä on funktion $f(x) = \cos \dfrac{x}{2}$ jakso?
VASTAUS
Funktion $f$ kuvaaja on C.
Funktion $g$ kuvaaja on A.
Funktion $h$ kuvaaja on B.
- Funktion $h(x) = 0{,}5\cos x$ suurin arvo on $0{,}5$ ja pienin $-0{,}5$. Sen jakso on $2\pi$.
- Funktion $g(x) = -\cos 4x$ suurin arvo on $1$ ja pienin $-1$. Neljä sen jaksoa mahtuu $2\pi$ mittaisen välin sisään, joten yhden jakson pituus on $\frac{2\pi}{4} = \frac{\pi}{2}$.
- Funktion $f(x) = \cos \frac{x}{2}$ jakso on $4\pi$.
Edellä on tutkittu kertoimien vaikutusta sini- ja kosinifunktioiden kuvaajiin. Tutkitaan vielä tämän kappaleen lopuksi, miten erilaiset vakiot vaikuttavat kosinifunktion kuvaajaan.
Vakioiden vaikutus kosinifunktioon
- Miten vakio $a$ vaikuttaa funktion $g(x) = \cos x + a$ kuvaajaan? Tutki asiaa tämän Geogebra-havainnollistuksen avulla.
- Miten vakio $a$ vaikuttaa funktion $f(x) = \cos (x+a)$ kuvaajaan? Tutki asiaa tämän Geogebra-havainnollistuksen avulla.
- Mikä pitää valita vakion $a$ arvoksi, jotta funktion $f(x)$ kuvaaja on sama kuin sinifunktion kuvaaja?
VASTAUS
- Kuvaaja siirtyy $y$-akselin suunnassa ylös tai alas.
- Kuvaaja siirtyy $x$-akselin suunnassa oikealle tai vasemmalle.
- Vakio $a = -\frac{\pi}{2} + n\cdot 2\pi$, missä $n$ on kokonaisluku. Siis $$ \cos \left(x -\frac{\pi}{2} + n \cdot 2\pi\right) = \sin x. $$
Sinin ja kosinin yhteyksiä
Suurin osa trigonometrian kaavoista voidaan johtaa seuraavaan teoreemaan koottujen niin sanottujen sinin ja kosinin summakaavojen avulla. Näiden summakaavojen yleispätevä ja yksityiskohtainen perustelu on sen verran työläs, että siihen ei tässä syvennytä. Sen sijaan tutkitaan, millaisia yhteyksiä sinin ja kosinin välille saadaan näiden summakaavojen avulla, ja harjoitellaan samalla kaavojen soveltamista. Kaavojen ulkoa opettelu ei ole tarpeen, koska ne voi tarvittaessa tarkistaa taulukkokirjasta tai netistä.
TEOREEMA
Kulmien $\alpha + \beta$ ja $\alpha - \beta$ sini ja kosini saadaan laskettua seuraavasti: \begin{align*} \sin(\alpha + \beta) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\[1mm] \sin(\alpha - \beta) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \\[1mm] \cos(\alpha + \beta) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\[1mm] \cos(\alpha - \beta) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{align*}
Yksikköympyrän ja Pythagoraan lauseen avulla perustellun teoreeman 7 nojalla tiedetään, että kaikilla kulmilla $x$ pätee $$ \sin^2\! x + \cos^2\! x = 1. $$ Seuraavassa tehtävässä tutkitaan sini- ja kosinifunktioiden yhteyttä toisesta näkökulmasta teoreeman 15 avulla. Tehtävä on jatkoa tehtävän 2.16 havainnoille.
Sinin ja kosinin yhteys
Sovella teoreemaa 15 ja sievennä mahdollisimman pitkälle lauseke
- $\cos \left(x -\dfrac{\pi}{2}\right)$
- $\sin \left(x + \dfrac{\pi}{2}\right)$.
VASTAUS
- \begin{align*} \cos \left(x -\tfrac{\pi}{2}\right) &= \cos x \cos \tfrac{\pi}{2} + \sin x \sin \tfrac{\pi}{2} \\ &= 0 + \sin x \cdot 1\\ &= \sin x \end{align*}
- \begin{align*} \sin \left(x +\tfrac{\pi}{2}\right) &= \sin x \cos \tfrac{\pi}{2} + \cos x \sin \tfrac{\pi}{2} \\ &= 0 + \cos x \cdot 1 \\ &= \cos x \end{align*}
Tehtävästä 2.17 saadaan seuraava teoreema, joka vahvistaa tehtävän 2.16 havainnon:
TEOREEMA
Kaikilla kulmilla $x$ pätee \begin{align*} \cos \left(x -\frac{\pi}{2}\right) &= \sin x \\[2mm] \sin \left(x + \frac{\pi}{2}\right) &= \cos x \end{align*}
Perustelu tehtävässä 2.17.
Teoreeman 16 mukaan kosinifunktio saa kaikki arvot $\frac{\pi}{2}$ verran ennen kuin sinifunktio: 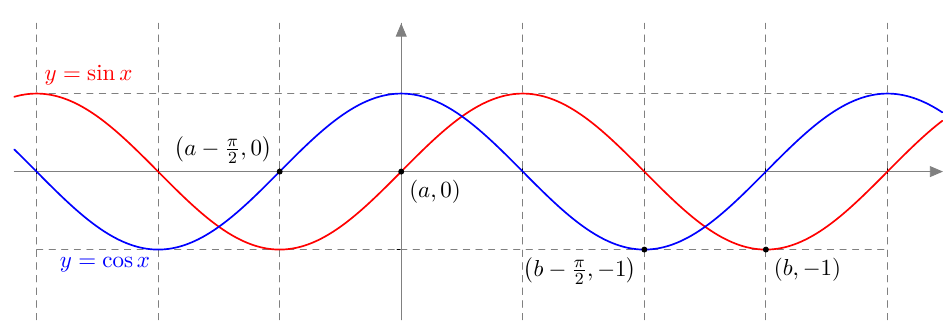 Vastaavasti sinifunktio saa kaikki arvot $\frac{\pi}{2}$ verran kosinifunktion jälkeen:
Vastaavasti sinifunktio saa kaikki arvot $\frac{\pi}{2}$ verran kosinifunktion jälkeen: 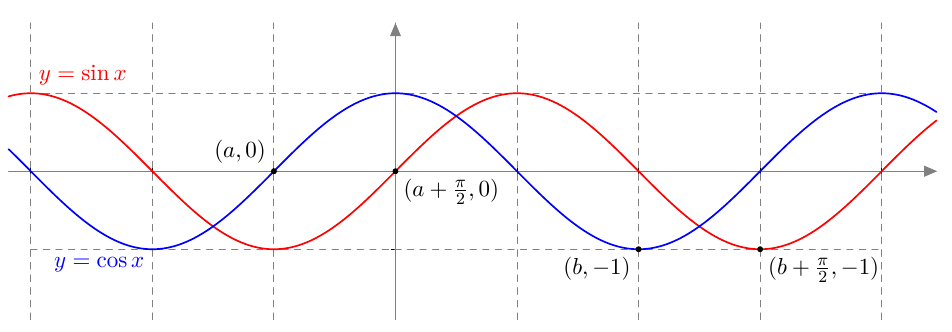 Sinifunktion ja kosinifunktion niin sanottu vaihe-ero on siis $\frac{\pi}{2}$ eli neljäsosa niiden jakson pituudesta.
Sinifunktion ja kosinifunktion niin sanottu vaihe-ero on siis $\frac{\pi}{2}$ eli neljäsosa niiden jakson pituudesta.
Tehtävissä 2.8 ja 2.15 tutkittiin erilaisten kertoimien vaikutusta sini- ja kosinifunktioiden jakson pituuteen. Seuraavaksi tutkitaan tarkemmin funktioita, jotka määritellään lausekkeilla $\sin 2x$ ja $\cos 2x$.
Funktio f(x) = sin 2x
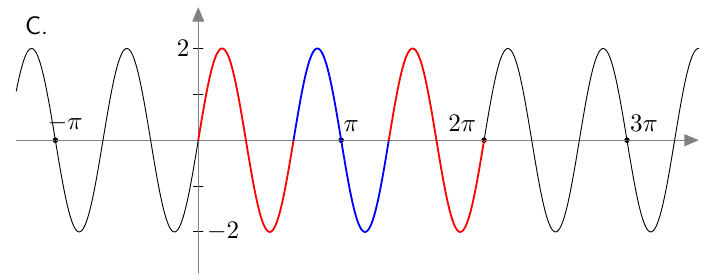
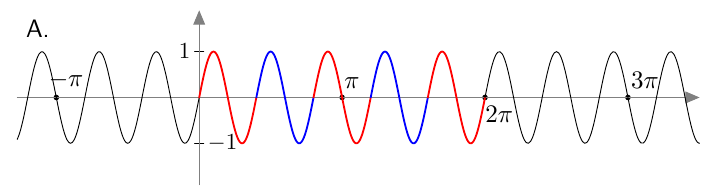
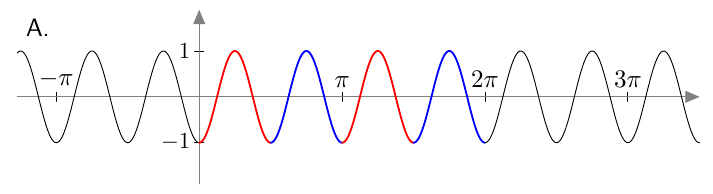
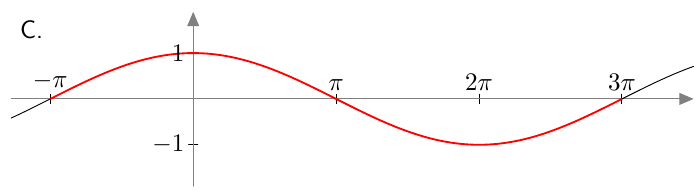
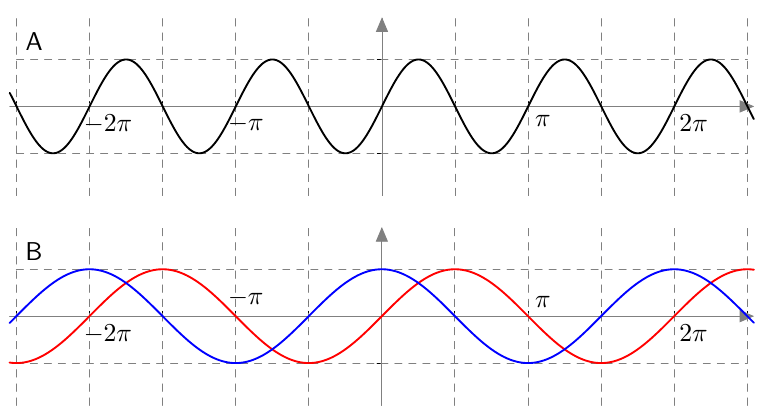
Alla on näkyvissä kolmen eri funktion kuvaajat.
- Kuvassa A on funktion $f(x) = \sin 2x$ kuvaaja. Mikä on sen jakson pituus?
- Kuvassa B on funktioiden $g(x) = \sin x$ ja $h(x) = \cos x$ kuvaajat. Minkä värinen on sinifunktion kuvaaja? Entä minkä värinen on kosinifunktion kuvaaja?
- Muodosta kuvan B funktioista $g(x) = \sin x$ ja $h(x) = \cos x$ jollakin laskutoimituksella uusi funktio $v(x)$, jolla on samat nollakohdat kuin kuvan A funktiolla.
Vinkki: MAA2-kurssin teoreema 4. - Piirrä funktion $v$ kuvaaja laskimella tai tietokoneella ja vertaa sitä kuvassa A näkyvään funktion $f(x) = \sin 2x$ kuvaajaan. Mitä havaitset?
- Mikä pitää valita kertoimen $k$ arvoksi, jotta $f(x) = k\cdot v(x)$?
Koordinaatiston ruudun leveys on $\frac{1}{2}\pi$ ja korkeus $1$.
VASTAUS
- Funktion $f(x) = \sin 2x$ jakson pituus on $\pi$.
- Sinifunktion kuvaaja on punainen, kosinifunktion kuvaaja on sininen.
- Yksi mahdollisuus on määritellä $v(x) = \sin x \cos x$.
- Keskellä kuvassa C näkyvissä funktion $v(x) = \sin x \cos x$ kuvaaja:
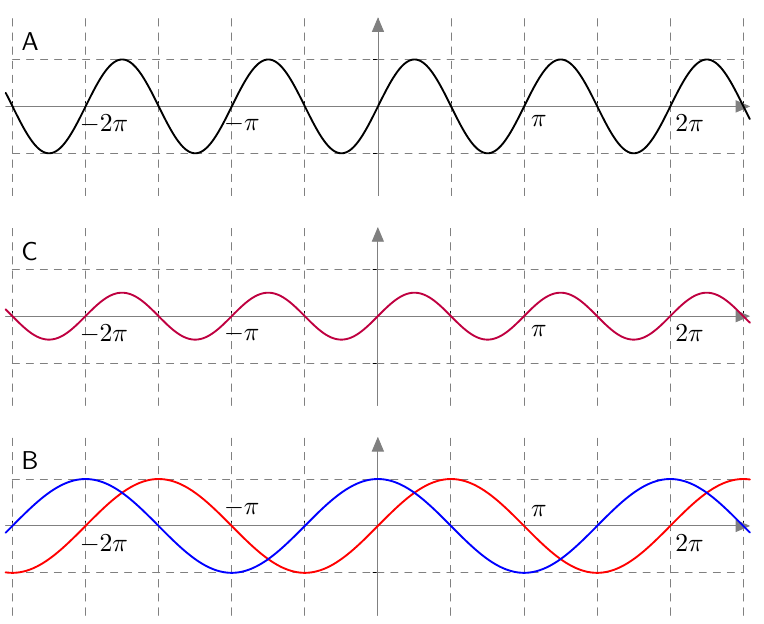
Havaitaan, että nollakohdat ovat oikein, mutta funktion suurin ja pienin arvo ovat itseisarvoltaan liian pieniä verrattuna funktion $f(x) = \sin 2x$ kuvaajaan. - Sopiva kerroin on $k = 2$. Siis $f(x) = 2v(x)$ eli $\sin 2x = 2\sin x\cos x$.
Funktio f(x) = cos 2x
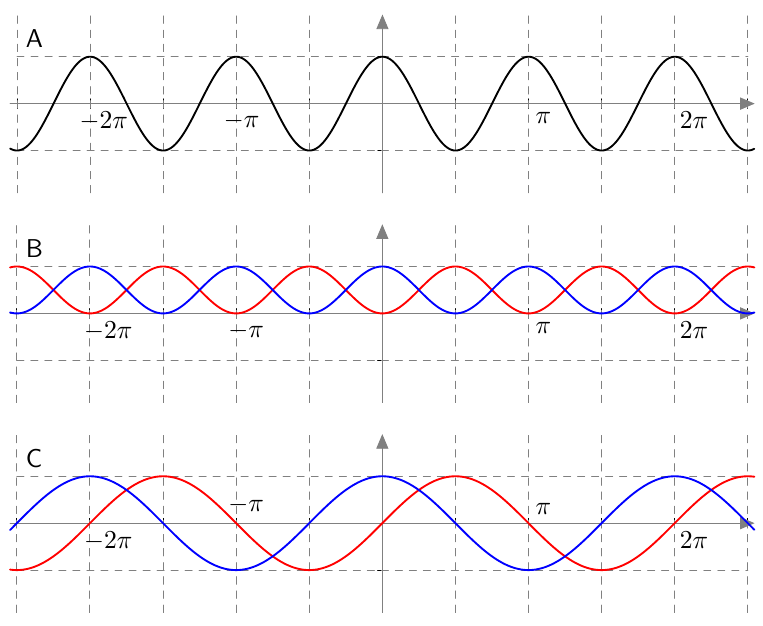
Alla on näkyvissä eri funktioiden kuvaajia.
- Ylimmässä kuvassa A on funktion $f(x) = \cos 2x$ kuvaaja. Mikä on sen jakson pituus?
- Alimmassa kuvassa C on funktioiden $g(x) = \sin x$ ja $h(x) = \cos x$ kuvaajat. Millä operaatiolla niistä saadaan muodostettua funktiot $v(x)$ ja $w(x)$, joiden kuvaajat ovat keskimmäisessä kuvassa B?
Vinkki: funktiot $v(x)$ ja $w(x)$ saavat vain epänegatiivisia arvoja, joten kannattaa miettiä, millaisten operaatioiden tulos on aina positiivinen tai nolla. - Muodosta kuvan B funktioista $v(x)$ ja $w(x)$ jollakin laskutoimituksella uusi funktio $s(x)$, jolla on samat nollakohdat kuin kuvan A funktiolla.
- Piirrä funktion $s$ kuvaaja laskimella tai tietokoneella ja vertaa sitä kuvassa A näkyvään funktion $f(x) = \cos 2x$ kuvaajaan. Mitä havaitset?
Koordinaatiston ruudun leveys on $\frac{1}{2}\pi$ ja korkeus $1$.
VASTAUS
- Funktion $f(x) = \cos 2x$ jakson pituus on $\pi$.
- Toiseen potenssiin korotus muuttaa negatiivisetkin arvot positiivisiksi: $v(x) = \sin^2\! x$ ja $w(x) = \cos^2\! x$.
Huomaa, että tässä käytetään jälleen potenssin lyhennysmerkintää: $\cos^2\! x = (\cos x)^2$ ja $\sin^2\! x = (\sin x)^2$. - \begin{align*} s(x) &= w(x) - v(x) \\[2mm] &= \cos^2\! x - \sin^2\! x \end{align*}
- Keskellä kuvassa D näkyvissä funktion $s(x) = \cos^2\! x - \sin^2\! x$ kuvaaja:
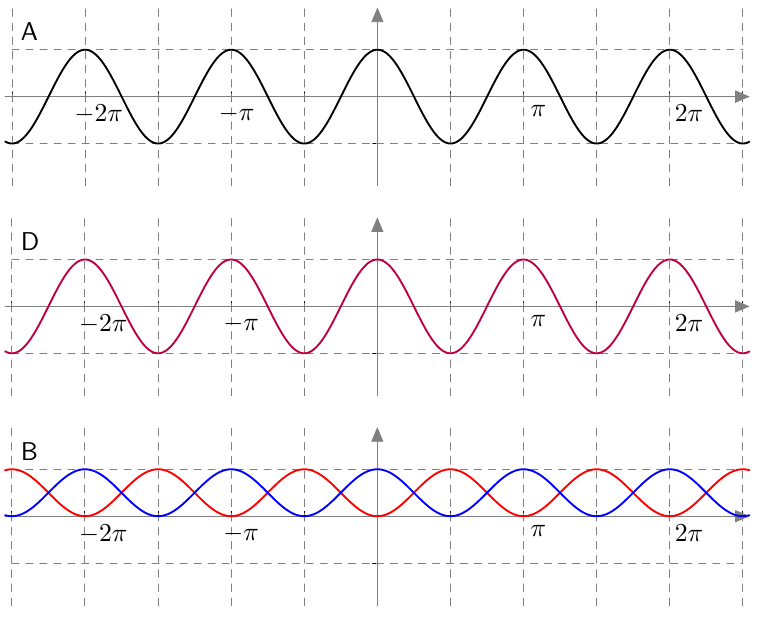
Havaitaan, että kuvien A ja D funktiot ovat samat. Siis $f(x) = w(x) - v(x)$ eli $\cos 2x = \cos^2\! x - \sin^2\! x$.
Edellisten tehtävien havainnot voidaan perustella yleispätevästi teoreeman 15 avulla.
Kaksinkertaisen kulman sini ja kosini
Sovella teoreemaa 15 ja sievennä mahdollisimman pitkälle lauseke
- $\sin 2x$
- $\cos 2x$.
Vinkki: miten voit kirjoittaa kulman $2x$ kahden kulman summana kirjainta $x$ käyttäen?
VASTAUS
- \begin{align*} \sin 2x &= \sin (x + x) \\ &= \sin x \cos x + \cos x \sin x \\ &= 2 \sin x \cos x \end{align*}
- \begin{align*} \cos 2x &= \cos(x + x) \\ &= \cos x \cos x - \sin x \sin x \\ &= \cos^2\! x - \sin^2\! x \end{align*}
Tehtävästä 2.20 saadaan seuraava teoreema:
TEOREEMA
Kulman $2x$ sini ja kosini saadaan laskettua kulman $x$ sinin ja kosinin avulla: \begin{align*} \sin 2x &= 2\sin x \cos x \\ \cos 2x &= \cos^2\! x - \sin^2\! x \end{align*}
Perustelu tehtävässä 2.20.
Seuraavissa tehtävissä harjoitellaan teoreeman 17 soveltamista.
Kaksinkertaisen kulman sini ja kosini
- Tiedetään, että $\pi < \alpha < \dfrac{3}{2}\pi$ ja $\sin \alpha = -\dfrac{1}{4}$. Määritä $\sin 2\alpha$.
- Tiedetään, että $\sin \beta = -\dfrac{3}{7}$. Määritä $\cos 2\beta$.
Vinkki: teoreema 7 tai Pythagoraan lause.
VASTAUS
- $\sin 2\alpha = \dfrac{\sqrt{15}}{8}$
- $\cos 2\beta = \dfrac{31}{49}$
Kaksinkertaisen kulman sini
Tehtävänä on ratkaista yhtälö $$ \sin 2x - \cos x = 0. $$
- Muokkaa yhtälö toiseen muotoon soveltamalla kaksinkertaisen kulman sinin kaavaa.
- Erota yhteinen tekijä ja sovella tulon nollasääntöä. Millaisiin yhtälöihin päädyt?
- Mitkä ovat yhtälön ratkaisut? Varmista yksikköympyrän avulla, että löydät kaikki ratkaisut.
VASTAUS
- $2\sin x\cos x - \cos x = 0$
- Yhtälö $\cos x (2\sin x - 1) = 0$ toteutuu, jos ja vain jos $\cos x = 0$ tai $2\sin x - 1 = 0$.
- Yhtälö totetuu, jos ja vain jos \begin{align*} x &= \dfrac{\pi}{2} + n \cdot \pi \ \text{ tai} \\[2mm] x &= \dfrac{\pi}{6} + n\cdot 2\pi \ \text{ tai} \\[2mm] x &= \dfrac{5\pi}{6} + n\cdot 2\pi, \end{align*} missä $n$ on kokonaisluku.
Tangenttifunktio
Edellisessä luvussa tangentti määriteltiin kaikille suunnatuille kulmille, joiden kehäpiste ei ole $y$-akselilla. Tämä tarkoittaa, että tangenttifunktio on määritelty, jos ja vain jos $x \neq \frac{\pi}{2} + n\pi$, missä $n$ on kokonaisluku. Tangenttifunktion kuvaaja saadaan muodostettua yksikköympyrän ja tangentin määritelmän avulla. Sitä tutkitaan seuraavassa tehtävässä.
Tangenttifunktion kuvaaja
Tutki tangettifunktion kuvaajaa tämän Geogebra-havainnollistuksen avulla. Päättele vastaukset seuraaviin kysymyksiin:
- Miten kulma $\alpha$ näkyy yksikköympyrässä? Entä tangenttifunktion kuvaajassa?
- Miten tangentin arvo $\tan\alpha$ näkyy yksikköympyrässä? Entä tangenttifunktion kuvaajassa?
- Missä $x$-akselin kohdissa tangenttifunktio ei ole määritelty?
- Missä $x$-akselin kohdissa tangenttifunktio saa arvon nolla?
- Miten kuvaajasta näkyy, että tangenttifunktio on jaksollinen funktio? Mikä on sen jakso?
VASTAUS
- Kulma $\alpha$ näkyy yksikköympyrässä suunnattuna kulmana ja tangenttifunktion kuvaajassa kuvaajan pisteen $x$-koordinaattina.
- Tangentin arvo $\tan\alpha$ on tangenttipisteen $y$-koordinaatti ja tangenttifunktion kuvaajan pisteen $y$-koordinaatti.
- Kohdissa $x = \frac{\pi}{2} + n\pi$, missä $n$ on kokonaisluku.
- Kohdissa $x = n\pi$, missä $n$ on kokonaisluku.
- Tangenttifunktion arvot toistuvat aina $\pi$ välein eli $\tan (x + \pi) = \tan x$ kaikilla kulmilla $x \neq \frac{\pi}{2} + n\pi$, $n \in \Z$.
Edellisen tehtävän havaintojen pohjalta saadaan seuraava teoreema:
TEOREEMA
Tangenttifunktio on määritelty, jos ja vain jos $$ x \neq \frac{\pi}{2} + n\pi, $$ missä $n$ on kokonaisluku. Tangenttifunktion arvojoukko on koko lukusuora $\R$.
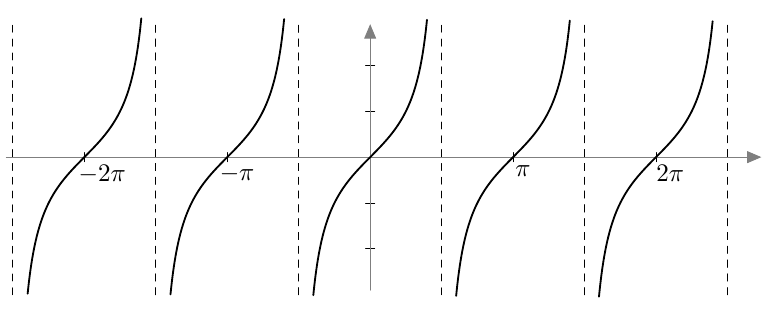
Tangenttifunktio on jaksollinen funktio. Sen jakso on $\pi$ eli määrittelyjoukossa kaikilla muuttujan $x$ arvoilla pätee $$ \tan(x + \pi) = \tan x. $$
Perustelu:
- Tangentin arvojoukkoa on tutkittu tehtävässä 1.28.
- Kulmilla $x$ ja $x + \pi$ on sama tangenttipiste, joten $\tan(x + \pi) = \tan x$.

Jatketaan vielä tangenttifunktion kuvaajan tutkimista.
Tangenttifunktion kuvaaja

Päättele yllä näkyvän tangenttifunktion kuvaajan avulla vastaukset seuraaviin kysymyksiin:
- Teoreeman 9 mukaan kulman ja sen vastakulman tangentit ovat toistensa vastalukuja eli $$\tan(-x) = -\tan x$$ kaikilla kulmilla $x$. Miten tämä näkyy tangenttifunktion kuvaajassa? Selitä omin sanoin.
- Onko tangenttifunktio jatkuva?
- Onko tangenttifunktio derivoituva?
VASTAUS
- Kuvaaja on symmetrinen origon suhteen:
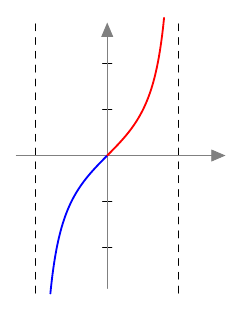
- Tangenttifunktion kuvaaja on katkematon käyrä kaikissa niissä kohdissa, joissa tangentti on määritelty, joten tangettifunktio on jatkuva.
- Tangenttifunktion kuvaajan jokaiseen pisteeseen voidaan asettaa tangentti tasan yhdellä tavalla, joten tangenttifunktio näyttäisi olevan derivoituva.
Kaksinkertaisen kulman tangentti
Tehtävänä on osoittaa, että kulman $2x$ tangentti saadaan kulman $x$ tangentista kaavalla $$ \tan 2x = \frac{2\tan x}{1 - \tan^2\! x}. $$ Tutkitaan yhtälön vasenta ja oikeaa puolta erikseen.
- Ilmaise $\tan 2x$ sinin ja kosinin avulla. Sovella sen jälkeen kaksinkertaisen kulman sinin ja kosinin kaavoja.
Vinkki: teoreemat 11 & 17. - Ilmaise $\tan x$ sinin ja kosinin avulla. Mihin muotoon lauseke $$ \frac{2\tan x}{1 - \tan^2\! x} $$ sievenee?
Vinkki: lavenna lausekkeella $\cos^2\! x$. - Vertaa a- ja b-kohdan tuloksia. Mitä huomaat?
VASTAUS
- \begin{align*} \tan 2x &= \frac{\sin 2x}{\cos 2x} \\[2mm] &= \frac{2\sin x\cos x}{\cos^2\! x - \sin^2\! x} \end{align*}
- \begin{align*} \frac{2\tan x}{1 - \tan^2\! x} &= \frac{2 \cdot \frac{\sin x}{\cos x}}{1 - \left(\frac{\sin x}{\cos x}\right)^2} \\[2mm] &= \frac{\cos^2\!x}{\cos^2\!x} \cdot \frac{2 \cdot \frac{\sin x}{\cos x}}{1 - \frac{\sin^2\! x}{\cos^2\! x}} \\[2mm] &= \frac{2\sin x\cos x}{\cos^2\! x - \sin^2\! x} \end{align*}
- Tulokset ovat samat, joten $$ \tan 2x = \frac{2\tan x}{1 - \tan^2\! x}. $$
Edellisen tehtävän tuloksesta saadaan seuraava teoreema:
TEOREEMA
Kulman $2x$ tangentti saadaan laskettua kulman $x$ tangentin avulla: $$ \tan 2x = \frac{2\tan x}{1 - \tan^2\! x}. $$
Perustelu tehtävässä 2.25.
Trigonometristen funktioiden derivaatat
Tässä kappaleessa tutkitaan sini-, kosini- ja tangenttifunktioiden derivaattafunktioita. Kurssissa MAA6 opittiin, että derivaatan arvo on funktion kuvaajalle asetetun tangentin kulmakerroin.
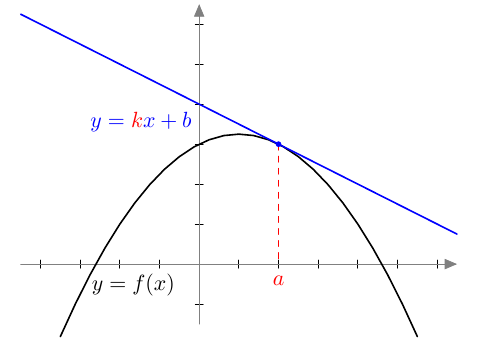
Kun määritetään tällaisen tangentin kulmakerroin $k$ mahdollisimman monessa kohdassa $a$ ja pisteet $(a,k)$ merkitään koordinaatistoon, piirtyy näkyviin derivaattafunktion kuvaaja. Seuraavissa tehtävissä hahmotellaan sinin ja kosinin derivaattafunktioiden kuvaajat tällä menetelmällä.
Sinifunktion derivaattafunktio
Tutki sinifunktion derivaattaa tämän Geogebra-havainnollistuksen avulla. Päättele vastaukset seuraaviin kysymyksiin:
- Miten oranssin pisteen $y$-koordinaatti ja tangentin kulmakerroin liittyvät toisiinsa?
- Miten sinifunktion kuvaajassa näkyvät ne kohdat, joissa derivaatta on
- nolla
- positiivinen
- negatiivinen?
- Miten derivaattafunktion kuvaajassa näkyvät ne kohdat, joissa derivaatta on
- nolla
- positiivinen
- negatiivinen?
- Tunnista derivaattafunktion kuvaajasta, mikä tuttu funktio se on.
VASTAUS
- Oranssin pisteen $y$-koordinaatti on samaan kohtaan piirretyn tangentin kulmakerroin. Oranssi piste on siis derivaattafunktion kuvaajan piste.
- Sinifunktion kuvaajalle piirretty tangentti on
- $x$-akselin suuntainen suora
- nouseva suora
- laskeva suora.
- Derivaattafunktion kuvaaja
- leikkaa $x$-akselin
- on $x$-akselin yläpuolella
- on $x$-akselin alapuolella.
- Sinifunktion derivaattafunktio on kosini eli $\mathrm{D} \sin x = \cos x$.
Kosinifunktion derivaattafunktio
Tutki kosinifunktion derivaattaa tämän Geogebra-havainnollistuksen avulla. Päättele vastaukset seuraaviin kysymyksiin:
- Miten oranssin pisteen $y$-koordinaatti ja kosinifunktion kuvaajalle piirretyn tangentin kulmakerroin liittyvät toisiinsa?
- Miten kosinifunktion kuvaajassa näkyvät ne kohdat, joissa derivaatta on
- suurimmillaan
- pienimmillään?
- Miten derivaattafunktion kuvaajassa näkyvät ne kohdat, joissa kosinifunktio saa
- suurimman arvonsa
- pienimmän arvonsa?
- Tunnista derivaattafunktion kuvaajasta, mikä funktio se on.
Vihje: Näkyvissä on myös sinifunktion kuvaaja. Miten se ja kosinin derivaattafunktio liittyvät toisiinsa?
VASTAUS
- Oranssin pisteen $y$-koordinaatti on samaan kohtaan piirretyn tangentin kulmakerroin. Oranssi piste on siis derivaattafunktion kuvaajan piste.
- Kosinifunktion kuvaaja
- nousee jyrkimmin
- laskee jyrkimmin.
- Molemmissa tapauksissa derivaattafunktion kuvaaja leikkaa $x$-akselin eli derivaatta saa arvon nolla.
- Kosinifunktion derivaattafunktio on sinifunktio kerrottuna luvulla $-1$ eli $\mathrm{D} \cos x = -\sin x$.
Sini- ja kosinifunktioiden derivaattafunktioiden muodostaminen derivaatan määritelmään nojautuen on sen verran työlästä, että tällä kurssilla tyydytään edellisten tehtävien havaintoihin.
TEOREEMA
Sini- ja kosinifunktiot ovat kaikkialla derivoituvia. Niiden derivaattafunktiot ovat \begin{align*} \mathrm{D} \sin x \, &= \cos x \\ \mathrm{D} \cos x &= - \sin x \end{align*}
Sinin ja kosinin derivaatat
Määritä seuraavat derivaatat:
- $\mathop{\mathrm{D}} \left(4 \cos x\right)$
- $\mathop{\mathrm{D}} \left(-\sqrt{2} \sin x \right)$
- $\mathop{\mathrm{D}} \left(\frac{3}{4}x^2 - 3\cos x \right)$
Vinkki: kertaa tarvittaessa derivointisääntöjä MAA6-kurssin luvusta 4.
VASTAUS
- $\mathop{\mathrm{D}} \left(4 \cos x\right) = -4\sin x$
- $\mathop{\mathrm{D}} \left(-\sqrt{2} \sin x\right) = -\sqrt{2} \cos x$
- $\mathop{\mathrm{D}} \left(\frac{3}{4}x^2 - 3\cos x \right) = \frac{3}{2}x + 3\sin x$
MAA6-kurssissa johdettuja derivointisääntöjä voidaan nyt soveltaa myös sini- ja kosinifunktioiden tuloihin, osamääriin ja potensseihin. Esimerkiksi funktion potenssin derivointisäännön $$ \mathop{\mathrm{D}} (f(x))^n = n(f(x))^{n-1}f'(x) $$ avulla voidaan määrittää funktion $g(x) = \sin^3\! x$ derivaatta. Huomaa, että tässä käytetään jälleen potenssin lyhennysmerkintää ja funktio $g$ on itse asiassa sinifunktion kolmas potenssi: $g(x) = (\sin x)^3$. Sen derivaataksi saadaan $$ g'(x) = 3\sin^2\! x\cos x. $$
Sinin ja kosinin derivaatat
Tehtävänä on määrittää funktion $h(x) = \cos^5\! x$ derivaattafunktio.
- Minkä funktion potenssista on kysymys? Jos ilmaiset funktion $h$ muodossa $h(x) = \left(f(x)\right)^n$, mitä ovat $f(x)$ ja $n$?
- Sovella funktion potenssin derivointisääntöä, jonka mukaan $$ \mathop{\mathrm{D}} (f(x))^n = n(f(x))^{n-1}f'(x). $$ Mitä derivointisäännössä esiintyvä $f'(x)$ on tämän tehtävän tilanteessa?
- Mikä on derivaattafunktio $h'(x)$?
VASTAUS
- Kysymyksessä on kosinifunktion viides potenssi. Siis $f(x) = \cos x$ ja $n = 5$.
- Derivointisäännön mukaan $\mathop{\mathrm{D}} \cos^5\! x = 5\cos^4\! x \cdot (-\sin x)$.
Tässä tapauksessa $f'(x) = -\sin x$. - $h'(x) = -5\cos^4\! x \sin x$
Sinin ja kosinin derivaatat
Määritä seuraavat derivaatat:
- $\mathop{\mathrm{D}} \sin^2\! x$
- $\mathop{\mathrm{D}} \left(2\cos^4\! x\right)$
- $\mathop{\mathrm{D}} \left(x \cos x\right)$
Vinkki: kertaa tarvittaessa derivointisääntöjä MAA6-kurssin luvusta 6.
VASTAUS
- $\mathop{\mathrm{D}} \sin^2\! x = 2\sin x\cos x$
- $\mathop{\mathrm{D}} \left(2\cos^4\! x\right) = -8\cos^3\! x \sin x$
- $\mathop{\mathrm{D}} \left(x \cos x\right) = \cos x - x\sin x$
Kun sinin ja kosinin derivaatat tunnetaan, saadaan johdettua lauseke tangenttifunktion derivaattafunktiolle. Tässä hyödynnetään MAA6-kurssissa perusteltua osamäärän derivointisääntöä $$\mathop{\mathrm{D}} \frac{f(x)}{g(x)} = \frac{f'(x)g(x)- f(x)g'(x)}{(g(x))^2}$$ sekä tämän kurssin teoreemaa 11, jonka mukaan kaikilla tangentin määrittelyjoukkoon kuuluvilla muuttujan $x$ arvoilla pätee $$ \tan x = \frac{\sin x}{\cos x}. $$
Tangenttifunktion derivaattafunktio
Tässä tehtävässä määritetään tangenttifunktion derivaattafunktio.
- Ilmaise tangenttifunktio sinin ja kosinin avulla. Sovella sen jälkeen osamäärän derivointisääntöä ja sievennä tulos.
Vinkki: edellisen luvun teoreema 11 ja MAA6-kurssin teoreema 15. - Millaiseen muotoon tangenttifunktion derivaattafunktio sievenee, jos sovellat kaavaa $\sin^2\! x + \cos^2\! x = 1$ (teoreema 7)?
- Millaiseen muotoon tangenttifunktion derivaattafunktio sievenee, jos suoritat jakolaskun termeittäin ja sovellat teoreemaa 11 toiseen suuntaan?
VASTAUS
- \begin{align*} \mathrm{D} \tan x &= \mathrm{D} \frac{\sin x}{\cos x} \\[2mm] &= \frac{\cos x\cos x - \sin x (-\sin x)}{\cos^2\! x} \\[2mm] &= \frac{\cos^2\! x + \sin^2\! x}{\cos^2\! x} \end{align*}
- \begin{align*} \mathrm{D} \tan x &= \frac{1}{\cos^2\! x} \end{align*}
- \begin{align*} \mathrm{D} \tan x &= \frac{\cos^2\! x}{\cos^2\! x} + \frac{\sin^2\! x}{\cos^2\! x} \\[2mm] &= 1 + \left(\frac{\sin x}{\cos}\right)^2 \\[2mm] &= 1 + \tan^2\! x \end{align*}
Edellisen tehtävän tuloksista saadaan seuraava teoreema:
TEOREEMA
Tangenttifunktio on derivoituva koko määrittelyjoukossaan. Sen derivaattafunktio on \begin{align*} \mathrm{D} \tan x \, &= \frac{1}{\cos^2\! x} \end{align*} tai toisin ilmaistuna \begin{align*} \mathrm{D} \tan x \, &= 1 + \tan^2\! x, \end{align*} missä $x \neq \frac{\pi}{2} + n\cdot \pi$ kaikilla kokonaisluvuilla $n$.
Perustelu tehtävässä 2.31.
Tangentin derivaatta
Määritä seuraavat derivaatat:
- $\mathop{\mathrm{D}} \left(\frac{1}{4}\tan^2\! x\right)$
- $\mathop{\mathrm{D}} \left(2\sin x - 3\tan x\right)$
- $\mathop{\mathrm{D}} \left(x^2 \tan x\right)$
VASTAUS
- $\mathop{\mathrm{D}} \left(\frac{1}{4}\tan^2\! x\right) = \frac{\tan x}{2\cos^2\! x}$
tai
$\mathop{\mathrm{D}} \left(\frac{1}{4}\tan^2\! x\right) = \frac{1}{2}\tan x(1 + \tan^2\! x)$ - $\mathop{\mathrm{D}} \left(2\sin x - 3\tan x\right) = 2\cos x - \frac{3}{\cos^2\! x}$
tai
$\mathop{\mathrm{D}} \left(2\sin x - 3\tan x\right) = 2\cos x - 3 - 3\tan^2\! x$ - $\mathop{\mathrm{D}} \left(x^2 \tan x\right) = 2x\tan x + \frac{x^2}{\cos^2\! x}$
tai
$\mathop{\mathrm{D}} \left(x^2 \tan x\right) = 2x\tan x + x^2(1 + \tan^2\! x)$
TEHTÄVÄSARJA II
Radiaani
Ilmaise kulman $\alpha$ suuruus asteina, jos sen suuruus radiaaneina on
- $\alpha = 0{,}59$
- $\alpha = -2{,}70$
- $\alpha = 13{,}01$
Anna vastaus yhtä monen merkitsevän numeron tarkkuudella kuin lähtöarvo.
Vastaus
- $\alpha \approx 34^\circ$ (kaksi merkitsevää numeroa)
- $\alpha \approx -155^\circ$ (kolme merkitsevää numeroa)
- $\alpha \approx 745{,}4^\circ$ (neljä merkitsevää numeroa)
Radiaani
Määritä tarkka arvo laskimen, taulukkokirjan tai yksikköympyrän ja muistikolmioiden avulla:
- $\sin \dfrac{\pi}{3}$
- $\cos \dfrac{5\pi}{4}$
- $\tan \dfrac{11\pi}{6}$
Vastaus
- $\sin \dfrac{\pi}{3} = \dfrac{\sqrt{3}}{2}$
- $\cos \dfrac{5\pi}{4} = -\dfrac{1}{\sqrt{2}}$
- $\tan \dfrac{11\pi}{6} = -\dfrac{1}{\sqrt{3}}$
Radiaani
Ilmaise kulman suuruus asteina, jos sen suuruus radiaaneina on
- $\dfrac{7\pi}{6}$
- $\dfrac{3\pi}{4}$
- $\dfrac{5\pi}{3}$
Vastaus
- $210^\circ$
- $135^\circ$
- $300^\circ$
Radiaani
Laske lausekkeen $$ \sin^2\! 2x + \cos x $$ arvo, jos
- $x = \dfrac{5\pi}{4}$
- $x = \dfrac{5\pi}{6}$
Vastaus
- $1 - \dfrac{1}{\sqrt{2}}$
- $\dfrac{3}{4} - \dfrac{\sqrt{3}}{2}$
Radiaani
Missä neljänneksessä kulman $x$ loppukylki on, jos
- $x = \dfrac{2\pi}{3}$
- $x = -\dfrac{5\pi}{4}$
- $x = \dfrac{7\pi}{3}$
- $x = 3{,}5$
- $x = -6{,}5$
Vastaus
- II neljänneksessä
- II neljänneksessä (huomaa, että kulma on negatiivinen)
- I neljänneksessä
- III neljänneksessä (huomaa, että oikokulma on $\pi \approx 3{,}14$)
- IV neljänneksessä (huomaa, että kulma on negatiivinen ja täyskulma on $2\pi \approx 6{,}28$)
Sinifunktio
Määritä funktion nollakohdat:
- $f(x) = \sin^2\! x - 1$
- $g(x) = \sin^3\! x - \sin x$
Vastaus
- $x = \dfrac{\pi}{2} + n\cdot \pi$, missä $n$ on kokonaisluku.
- $x = n\cdot \dfrac{\pi}{2}$, missä $n$ on kokonaisluku.
Sinifunktio
Päättele funktion suurin ja pienin arvo. Millä muuttujan arvoilla funktio saa suurimman ja millä pienimmän arvonsa?
- $f(x) = 4\sin 3x$
- $g(x) = 7 - 3\sin 2x$
Vinkki: hyödynnä teoreemaa 13 tai teoreemaa 1.
Vastaus
- Suurin arvo on $4$ ja se saavutetaan kohdissa $x = \frac{\pi}{6} + n\cdot \frac{2\pi}{3}$, missä $n$ on kokonaisluku.
Pienin arvo on $-4$ ja se saavutetaan kohdissa $x = \frac{\pi}{2} + n\cdot \frac{2\pi}{3}$, missä $n$ on kokonaisluku. - Suurin arvo on $10$ ja se saavutetaan kohdissa $x = \frac{3\pi}{4} + n\cdot \pi$, missä $n$ on kokonaisluku.
Pienin arvo on $4$ ja se saavutetaan kohdissa $x = \frac{\pi}{4} + n\cdot \pi$, missä $n$ on kokonaisluku.
Sinifunktio
Suurin osa kotitalouksien ja teollisuuden käyttämästä sähköenergiasta siirretään voimalaitosten generaattoreista käyttäjille vaihtovirran avulla. Suomessa verkkojännite vaihtelee noudattaen funktiota $$ U(t) = 325 \text{ V} \cdot \sin(100\pi t), $$ missä $t$ on aika sekunteina ilmaistuna ja V tarkoittaa jännitteen yksikköä (voltti).
Selvitä funktion lausekkeen avulla,
- mikä on jännitteen suurin arvo ja mikä pienin
- mitä ovat ne ajanhetket, jolloin jännitteen arvo on nolla
- mikä on funktion jakson pituus.
Vastaus
- Jännitteen suurin arvo on 325 V ja pienin -325 V.
- Jännite on nolla hetkillä $t = n \cdot 0{,}01$ s, missä $n$ on kokonaisluku, eli sekunnin sadasosan välein.
- Sinifunktion jakson pituus on nollakohtien välimatka kaksinkertaisena eli tässä tapauksessa 0,02 sekuntia.
Sinifunktio
Määritä funktion $$ f(x) = 6 - 7\sin^2\! x $$ suurin ja pienin arvo.
Vastaus
Koska $0 \leq \sin^2\! x \leq 1$ kaikilla kulmilla $x$, niin funktion $f$ suurin arvo on $6$ ja pienin arvo on $-1$.
Sinifunktio
Kun vuorovesi-ilmiötä tutkittiin Fundynlahdella Kanadan itärannikolla, havaittiin että veden syvyyttä (metreinä) voidaan mittauspaikkassa kuvata funktiolla $$ f(t) = 6{,}5 + 5\sin\left(\frac{2\pi t}{12{,}27} + \pi\right), $$ missä aika $t$ ilmoitetaan tunteina.
- Millä välillä veden syvyys vaihtelee?
- Kuinka pitkä veden syvyysvaihtelun jakso?
- Kuinka pitkän aikaa voi mittauspaikalla viettää laiva, jonka syväys on 8 metriä?
Vastaus
- Syvyys on pienimmillään 1,5 metriä ja suurimmillaan 11,5 metriä.
- Jakso on 12,27 tuntia. Tämän voi päätellä esimerkiksi siitä, että vesi on syvimmillään, kun sini saa arvon yksi eli $$ \frac{2\pi t}{12{,}27} + \pi = \frac{\pi}{2} + n \cdot 2\pi, $$ missä $n$ on kokonaisluku, ja vastaavat ajanhetket ovat $$ t \approx -3{,}068 + n \cdot 12{,}27. $$ Vesi saavuttaa suurimman syvyyden siis aina 12,27 tunnin välein.
- Yhtälö $$ 6{,}5 + 5\sin\left(\frac{2\pi t}{12{,}27} + \pi\right) = 8 $$ toteutuu, jos ja vain jos $$ t \approx -5{,}540 + n \cdot 12{,}27 $$ tai $$ t \approx -0{,}595 + n \cdot 12{,}27 $$ missä $n$ on kokonaisluku. Veden syvyys on vähintään 8 metriä välillä $[-5{,}540, -0{,}595]$ eli noin 4,95 tuntia (4 h 57 min).
Kosinifunktio
Määritä funktion nollakohdat:
- $f(x) = \cos^2\! x + \cos x$
- $g(x) = \sqrt{3} - 2\cos 4x$
Vastaus
- $x = \dfrac{\pi}{2} + n \cdot \pi$ tai $x = \pi + n \cdot 2\pi$, missä $n$ on kokonaisluku.
- $x = \dfrac{\pi}{24} + n \cdot \dfrac{\pi}{2}$ tai $x = -\dfrac{\pi}{24} + n \cdot \dfrac{\pi}{2}$, missä $n$ on kokonaisluku.
Kosinifunktio
Millä muuttujan arvoilla funktioiden $f(x) = \cos 3x$ ja $g(x) = \cos 4x$ arvot ovat yhtä suuret? Mitkä näistä muuttujan arvoista ovat välillä $[0, 2\pi\pe$?
Vastaus
Arvoilla $x = n \cdot \dfrac{2\pi}{7}$, missä $n$ on kokonaisluku. Näistä välillä $[0, 2\pi\pe$ ovat $0$, $\dfrac{2\pi}{7}$, $\dfrac{4\pi}{7}$, $\dfrac{6\pi}{7}$, $\dfrac{8\pi}{7}$, $\dfrac{10\pi}{7}$, $\dfrac{12\pi}{7}$.
Kosinifunktio
Sataman veden syvyys vaihtelee nousu- ja laskuveden myötä 12 tunnin jaksoissa. Syvyys on suurimmillaan 5,2 metriä ja pienimmillään 2,4 metriä. Laadi veden syvyyden laskemiseksi matemaattinen malli, jossa muuttujana on aika $t$ (tunteina), ja hetkellä $t = 0$ vesi on korkeimmillaan. Kuinka monta tuntia vuorokaudesta veden syvyys on vähintään 3,0 metriä?
Vastaus
Veden syvyyttä (metreinä) voidaan kuvata funktiolla $$ f(t) = 3{,}8 + 1{,}4 \cos \left(\dfrac{\pi t}{6}\right). $$ Yhtälön $$ 3{,}8 + 1{,}4 \cos \left(\dfrac{\pi t}{6}\right) = 3{,}0 $$ ratkaisut ovat $$ t \approx \pm 4{,}2 + 12n, $$ missä $n$ on kokonaisluku. Välillä $[0, 24\pe$ näistä ovat $4{,}2$; $7{,}8$; $16{,}2$ ja $19{,}8$. Voidaan päätellä, että veden syvyys on vähintään 3,0 metriä 4,2 tuntia nousuveden huipun molemmin puolin eli vuorokaudessa yhteensä $2\cdot 8{,}4 = 16{,}8$ tuntia. (Huom. nousuveden huippu ajanhetkinä $t = 0$ ja $t = 12$.)
Kosinifunktio
Määritä funktion suurin ja pienin arvo välillä $-\dfrac{\pi}{4} < x \leq \dfrac{4\pi}{3}$:
- $f(x) = \dfrac{1}{4-\cos x}$
- $g(x) = 3 - 10\cos \dfrac{x}{2}$
Vastaus
- Suurin arvo on $f(0) = \frac{1}{3}$ ja pienin arvo on $f(\pi) = \frac{1}{5}$.
- Suurin arvo on $g\left(\frac{4\pi}{3}\right) = 8$ ja pienin arvo on $g(0) = -7$.
Sinin ja kosinin yhteyksiä
- Millä muuttujan $x$ arvoilla funktioiden $f(x) = \sin^2\! x$ ja $g(x) = 3\cos^2\! x$ ovat yhtä suuret?
- Keksi toinen tapa ratkaista a-kohdan tehtävä.
Vastaus
- $x = \dfrac{\pi}{3} + n \cdot \pi$ tai $x = -\dfrac{\pi}{3} + n \cdot \pi$, missä $n$ on kokonaisluku.
- Yksi mahdollisuus on käyttää teoreemaa 7 ja muokata yhtälö muotoon $$ 1 - \cos^2\! x = 3\cos^2\! x. $$ Toinen mahdollisuus on muokata yhtälö muotoon $$ \dfrac{\sin^2\! x}{\cos^2\! x} = 3 $$ ja käyttää teoreemaa 11.
Sinin ja kosinin yhteyksiä
Ratkaise yhtälö $$ \cos 2x = 3\cos x - 2. $$ Vinkki: teoreema 17 ja teoreema 7.
Vastaus
Sinin ja kosinin yhteyksiä
Tehtävänä on määrittää alla näkyvän kolmion kulman $\sphericalangle CAB$ tangentin tarkka arvo.
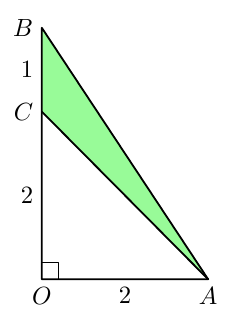
- Merkitään $\alpha = \sphericalangle OAB$ ja $\beta = \sphericalangle OAC$. Ilmaise kulma $\sphericalangle CAB$ kulmien $\alpha$ ja $\beta$ avulla.
- Määritä kulman $\sphericalangle CAB$ sinin ja kosinin arvot teoreeman 15 avulla.
- Mikä on kulman $\sphericalangle CAB$ tangentin arvo?
Vastaus
- $\sphericalangle CAB = \alpha - \beta$
- \begin{align*} \sin (\alpha - \beta) &= \frac{1}{\sqrt{2}\sqrt{13})} \\[2mm] \cos (\alpha - \beta) &= \frac{5}{\sqrt{2}\sqrt{13})} \end{align*}
- $\tan (\alpha - \beta) = \dfrac{1}{5}$
Sinin ja kosinin yhteyksiä
Suorakulmaisen kolmion terävät kulmat ovat $\alpha$ ja $\beta$. Tehtävänä on osoittaa, että $$ \sin(\alpha + \beta) < \sin \alpha + \sin \beta. $$
- Ilmaise lauseke $\sin(\alpha + \beta)$ toisella tavalla teoreeman 15 avulla.
- Mitä pystyt tehtävän tilanteessa päättelemään luvuista $\cos \alpha$ ja $\cos \beta$? Kuinka suuria ovat niiden mahdolliset arvot?
- Kirjoita a- ja b-kohtien avulla perustelu väitteelle, jonka mukaan suorakulmaisen kolmion teräville kulmille $\alpha$ ja $\beta$ pätee epäyhtälö $$ \sin(\alpha + \beta) < \sin \alpha + \sin \beta. $$
- Keksi esimerkki, joka osoittaa, että tämän tehtävän epäyhtälö ei päde kaikilla kulmilla $\alpha$ ja $\beta$.
Vastaus
- $\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta$
- Koska $0 < \alpha < \frac{\pi}{2}$, niin $0 < \cos \alpha < 1$. Vastaavasti koska $0 < \beta < \frac{\pi}{2}$, niin $0 < \cos \beta < 1$.
- Edellisten kohtien avulla saadaan pääteltyä, että \begin{align*} \sin(\alpha + \beta) &= \sin\alpha\cos\beta + \cos\alpha\sin\beta \\ &< (\sin \alpha) \cdot 1 + 1\cdot \sin \beta \\ &= \sin \alpha + \sin \beta \end{align*}
- Valitaan esimerkiksi $\alpha = \frac{3\pi}{2}$ ja $\beta = \frac{3\pi}{2}$. Tällöin $\sin(\alpha + \beta) = \sin 3\pi = 0$ ja $\sin \alpha + \sin \beta = -1 + (-1) = -2$. Siis $$ \sin(\alpha + \beta) \not < \sin \alpha + \sin \beta. $$
Sinin ja kosinin yhteyksiä
Määritä funktion $$ f(x) = (\sin x + \cos x)^2 - 5 $$ arvojoukko. Onko funktio jaksollinen? Myönteisessä tapauksessa selvitä sen jakson pituus.
Vinkki: teoreemat 7 ja 17.
Vastaus
Funktio voidaan esittää muodossa $$ f(x) = \sin 2x - 4. $$ Tästä voidaan päätellä, että funktion arvojoukko on suljettu väli $[-5,-3]$. (Huomaa, että $\sin 2x$ saa kaikki arvot välillä $[-1,1]$.)
Funktio on jaksollinen ja sen jakso on puolet tavallisen sinifunktion jaksosta eli $\pi$.
Tangenttifunktio
Määritä funktion $$ f(x) = \tan 4x - 1 $$ määrittelyjoukko, arvojoukko ja nollakohdat.
Vastaus
Arvojoukko on koko reaalilukujen joukko $\R$.
Nollakohdat ovat $x \neq \frac{\pi}{16} + n \cdot \frac{\pi}{4}$, missä $n$ on kokonaisluku.
Tangenttifunktio
Määritä funktion $$ g(x) = \tan 2x $$ tarkka arvo, jos $\sin x = -\dfrac{8}{17}$ ja $\pi < x < \dfrac{3\pi}{2}$.
Vinkki: teoreema 19.
Vastaus
Trigonometristen funktioiden derivaatat
Määritä funktion $$ f(x) = 5\sqrt{2}\sin x + \sqrt{2}\cos x $$ kuvaajalle kohtaan $x = \frac{3\pi}{4}$ piirretyn tangentin yhtälö.
Vinkki: kertaa tarvittaessa MAA6-kurssin luku 1 sekä MAA5-kurssin teoreema 9.
Vastaus
Trigonometristen funktioiden derivaatat
Osoita, että funktio $$ f(x) = \frac{1}{3}x^3 + x - \cos x $$ on kaikkialla aidosti kasvava.
Vinkki: kertaa tarvittaessa MAA6-kurssin teoreema 10.
Vastaus
Trigonometristen funktioiden derivaatat
Määritä funktion $$ f(x) = \sin^2\! x + 2\cos x $$ suurin ja pienin arvo.
Vastaus
Funktion suurin arvo on $2$ ja funktio saa sen kohdissa $x = n \cdot 2\pi$, missä $n$ on kokonaisluku.
Funktion pienin arvo on $-2$ ja funktio saa sen kohdissa $x = \pi + n \cdot 2\pi$, missä $n$ on kokonaisluku.
Trigonometristen funktioiden derivaatat
Määritä funktion $$ g(x) = \frac{\sin x}{2 - \cos x} $$ suurin ja pienin arvo.
Vastaus
Funktion suurin arvo on $\drac{\sqrt{3}}{3}$ ja funktio saa sen kohdissa $x = \dfrac{\pi}{3} + n \cdot 2\pi$, missä $n$ on kokonaisluku.
Funktion pienin arvo on $-\drac{\sqrt{3}}{3}$ ja funktio saa sen kohdissa $x = \dfrac{5\pi}{3} + n \cdot 2\pi$, missä $n$ on kokonaisluku.
Trigonometristen funktioiden derivaatat
Puoliympyrässä, jonka säde on 1, on tasakylkinen puolisuunnikas, jonka yhtenä sivuna on ympyrän halkaisija.
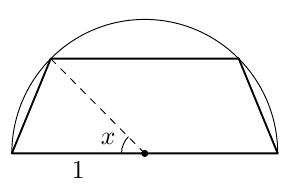
- Määritä puolisuunnikkaan suurin mahdollinen pinta-ala.
- Kuinka monta prosenttia suurimman puolisuunnikkaan pinta-ala on puoliympyrän pinta-alasta?
Vinkki: kertaa tarvittaessa MAA3-kurssin teoreemat 10 ja 13.
Vastaus
- Puolisuunnikkaan suurin mahdollinen pinta-ala on $$ \frac{3\sqrt{3}}{4}. $$ Puolisuunnikkaan pinta-ala on $$ A(x) = \sin x \cos x + \sin x, $$ missä kulma $x$ on välillä $\left[0, \frac{\pi}{2}\right]$. Sen derivaattafunktio on \begin{align*} A'(x) &= \cos^2\! x - \sin^2\! x + \cos x \\ &= 2\cos^2\! x - 1 + \cos x. \end{align*} Derivaattafunktiolla on välillä $\left[0, \frac{\pi}{2}\right]$ yksi nollakohta $x = \frac{\pi}{3}$. Suljetulla välillä $\left[0, \frac{\pi}{2}\right]$ funktio $A$ saa suurimman arvonsa derivaatan nollakohdassa tai välin päätepisteissä. Koska $A(0) = 0$, $A\left(\frac{\pi}{2}\right) = 1$ ja $A\left(\frac{\pi}{3}\right) = \frac{3\sqrt{3}}{4} \approx 1{,}3$, pinta-alan suurin arvo on $$ \frac{3\sqrt{3}}{4}. $$
- Noin 83 %.
Trigonometristen funktioiden derivaatat
Rannassa sijaitsevalta muuntajalta $A$ aiotaan vetää sähkökaapeli saareen $B$. Kaapelointikustannukset kilometriä kohden ovat merellä 2,5-kertaiset verrattuna kaapelointikustannuksiin maalla. Määritä kaapelin reitti niin, että kokonaiskustannukset ovat mahdollisimmat pienet. Ratkaise ongelma valitsemalla muuttujaksi kulma.
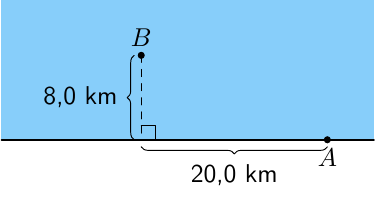
Vastaus
Kaapeli kannattaa vetää muuntajalta $A$ rantaa pitkin pisteeseen $P$, joka on 16,5 km etäisyydellä muuntajasta, ja tästä suoraan saareen.
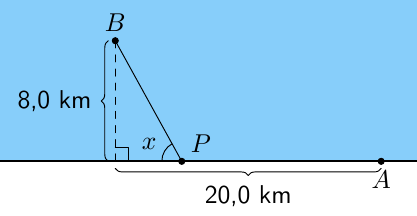
Koska kustannukset merellä kilometriä kohden ovat 2,5-kertaiset verrattuna kaapelointikustannuksiin maalla, voidaan tutkia funktiota $$ f(x) = 2{,}5\cdot \frac{8}{\sin x} + 20 - \frac{8}{\tan x}, $$ missä kulma $x$ on välillä $\left[0, \frac{\pi}{2}\right]$. Sen derivaattafunktio on \begin{align*} f'(x) &= \frac{-20\cos x}{\sin^2\! x} + \frac{8(1 + \tan^2\! x)}{\tan^2\! x}\\[2mm] &= \frac{-20\cos x}{\sin^2\! x} + \frac{8}{\tan^2\! x} + 8 \\[2mm] &= \frac{-20\cos x}{\sin^2\! x} + \frac{8\cos^2\! x}{\sin^2\! x} + \frac{8\sin^2\! x}{\sin^2\! x} \\[2mm] &= \frac{-20\cos x + 8}{\sin^2\! x}. \end{align*} Derivaattafunktiolla on välillä $\left[0, \frac{\pi}{2}\right]$ yksi nollakohta $x \approx 1{,}159$. Esimerkiksi kulkukaavion avulla havaitaan, että funktio $f$ saa siinä pienimmän arvonsa välillä $\left[0, \frac{\pi}{2}\right]$.
Huom. tehtävän voi ratkaista myös ottamalla muuttujaksi kulman, jonka kärki on pisteessä $B$. Sievennykset ovat silloin vähän helpompia.
Trigonometristen funktioiden derivaatat
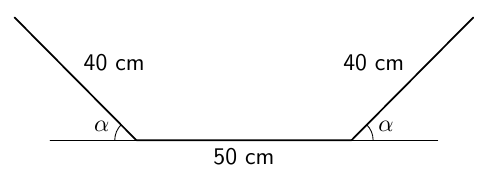
Säiliön pohja ja sivut tehdään 1,30 metrin levyisestä metallilevystä taivuttamalla levyn sivuilta 40 cm levyiset kaistaleet ylöspäin. Määritä taivutuskulma $\alpha$ asteen tarkkuudella niin, että säiliön tilavuus on mahdollisimman suuri.
Vastaus
Säiliön tilavuus on suurin, kun taivutuskulma on noin 58 astetta.

Säiliön poikkileikkauksen pinta-alan ilmaisee funktio $$ A(x) = 2000 \sin x + 1600\sin x\cos x, $$ missä kulma x on välillä $\left[0, \frac{\pi}{2}\right]$. Sen derivaattafunktiolla \begin{align*} A'(x) &= 2000 \cos x - 1600 \sin^2\! x + 1600 \cos^2\! x \\ &= 2000 \cos x + 3200 \cos^2\! x - 1600 \end{align*} on välillä $\left[0, \frac{\pi}{2}\right]$ yksi nollakohta $x \approx 1{,}0184$. Esimerkiksi kulkukaavion avulla havaitaan, että funktio $A$ saa siinä suurimman arvonsa välillä $\left[0, \frac{\pi}{2}\right]$.
Trigonometristen funktioiden derivaatat
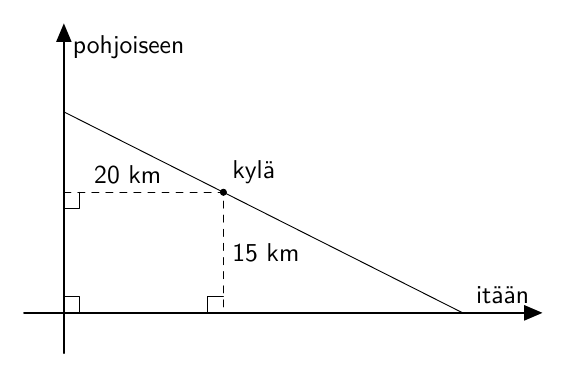
Kylän etäisyys toisesta kohtisuoraan risteävästä tiestä on 20,0 km ja toisesta 15,0 km. Kylän kautta suunnitellaan rakennettavaksi teitä yhdistävä suora yhdystie. Kuinka pitkä lyhin mahdollinen tie on? Missä kohdassa lyhin tie erkaantuu itään kulkevalta tieltä?
Ratkaise ongelma valitsemalla muuttujaksi kulma.
Vastaus
Lyhin tie on noin 49,3 km pitkä ja se erkanee itään kulkevalta tieltä noin 36,5 km risteyksestä itään.
Jos $x$ on yhdystien ja itään kulkevan tien välinen terävä kulma, niin tien pituus on $$ f(x) = \frac{15}{\sin x} + \frac{20}{\cos x}, $$ missä $x$ on välillä $\left]0, \frac{\pi}{2}\right[$. Derivaattafunktion \begin{align*} f'(x) &= -\frac{15\cos x}{\sin^2\! x} + \frac{20\sin x}{\cos^2\! x} \\[2mm] &= \frac{-15\cos^3\! x + 20 \sin^3\! x}{\sin^2\! x\cos^2\! x} \end{align*} arvo on nolla, jos ja vain jos osoittaja on nolla eli $$ \tan^3\! x = \frac{3}{4}. $$ Tarkasteluvälillä on yksi nollakohta $x \approx 0{,}7375$. Kun laaditaan kulkukaavio, havaitaan, että funktio $f$ saa tässä derivaatan nollakohdassa pienimmän arvonsa.
Trigonometristen funktioiden derivaatat
Paikka A on 13,0 km etäisyydellä paikoista B ja C, joiden välimatka on 10,0 km. Nämä kolme paikkaa halutaan yhdistää toisiinsa pisteestä P alkavilla valokuitukaapeleilla niin, että kaapelit $PB$ ja $PC$ ovat yhtä pitkiä. Tehtävänä on määrittää tällaiseen kytkentään tarvittavan valokuitukaapelin pienin mahdollinen määrä.
- Piirrä tilanteesta mallikuva. Määritä kolmion $ABC$ korkeusjanan pituus.
- Valitse muuttujaksi esimerkiksi kulma $x = \sphericalangle CBP$. Ilmaise janan $PB$ pituus kulman $x$ avulla.
- Ilmaise janan $AP$ pituus kulman $x$ avulla.
Vinkki: Hyödynnä suorakulmaista kolmiota $BPD$, missä $D$ on janan $BC$ keskipiste. Muista, että a-kohdassa selvitit kolmion $ABC$ korkeusjanan pituuden. - Muodosta funktio $f$, joka ilmaisee valokuituverkon pituuden. Millä välillä kulma $x$ voi tehtävän tilanteessa vaihdella?
- Määritä funktion $f$ pienin arvo tarkasteluvälillä.
Vastaus
- Mallikuva
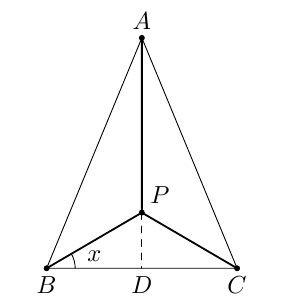
Korkeusjanan pituus on $\left| AD \right| = \sqrt{13^2 - 5^2} = 12$. - $\left| PB \right| = \dfrac{5}{\cos x}$
- $\left| AP \right| = 12 - 5\tan x$
- $f(x) = 2\cdot \dfrac{5}{\cos x} - 5\tan x$, missä $0 \leq x \lesssim 1{,}18$.
- Derivaattafunktiolla \begin{align*} f'(x) &= \frac{10\sin x}{\cos^2\! x} - \frac{5}{\cos^2\! x} \\[2mm] &= \frac{10\sin x - 5}{\cos^2\! x} \end{align*} on tarkasteluvälillä nollakohta $$ x = \frac{\pi}{6}. $$ Funktio $f$ saa pienimmän arvonsa joko derivaatan nollakohdassa tai tarkasteluvälin päätepisteissä. Derivaatan nollakohdassa sen arvo on $$ f\left(\frac{\pi}{6}\right) \approx 20{,}7. $$ Tarkasteluvälin päätepisteissä joko $P = D$ tai $P = A$. Tällöin funktion arvo on joko $12 + 10 = 22$ tai $2\cdot 13 = 26$. Valokuitukaapelin pienin tarvittava määrä on siis noin 20,7 km.
TEHTÄVÄSARJA III
Piirrä kolme yksikköympyrää ja merkitse niihin seuraavat kulmat ja vastaavat kehäpisteet:
- $405^\circ$
- $-120^\circ$
- $\dfrac{3\pi}{4}$ rad.
[Pitkä K2015/1]
Vastaus
- Kulma $\alpha$ toteuttaa ehdot $-\dfrac{\pi}{2} < \alpha < \dfrac{\pi}{2}$ ja $\sin \alpha = \dfrac{1}{4}$. Määritä luvun $\cos \alpha$ tarkka arvo.
- Olkoon $\alpha \in \left[\pi, \dfrac{3\pi}{2} \right]$ sellainen kulma, että $\cos \alpha = -\dfrac{1}{3}$. Määritä lukujen $\sin \alpha$ ja $\tan \alpha$ tarkat arvot.
- Sievennä lauseke $\sin^2\! x + \cos^2 (x + 2\pi)$.
[Pitkä K2013/2c & S2012/4a & K2012/2d]
Vastaus
- $\cos \alpha = \dfrac{\sqrt{15}}{4}$
- $\sin \alpha = -\dfrac{2\sqrt{2}}{3}$ ja $\tan \alpha = 2\sqrt{2}$
- $1$
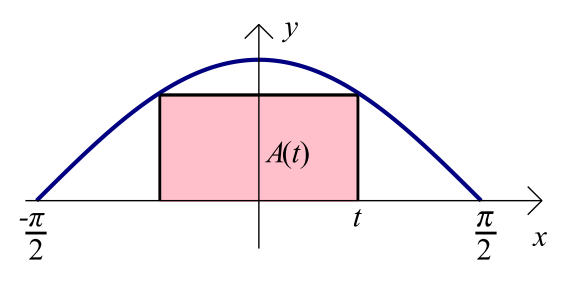
Suorakulmion yksi sivu on $x$-akselilla ja kaksi kärkeä käyrällä $y = \cos x$, kun $-\frac{\pi}{2} < x < \frac{\pi}{2}$.
- Muodosta lauseke suorakulmion pinta-alalle $A(t)$ kuvioon merkityn muuttujan $0 < t < \frac{\pi}{2}$ funktiona.
- Ratkaise funktion $A(t)$ derivaatan nollakohta kahden desimaalin tarkkuudella käyttämällä valitsemaasi numeerista menetelmää.
- Määritä suurimman mahdollisen suorakulmion pinta-alan likiarvon yhden desimaalin tarkkuudella.
[Pitkä K2013/12]
Vastaus
- Pinta-ala on $A(t) = 2t\cos t$.
- Derivaattafunktio on $$A'(t) = -2t\sin t + 2\cos t.$$ Sen nollakohta löydetään esimerkiksi haarukoimalla. Havaitaan, että $$A'(0{,}864) < 0$$ ja $$A'(0{,}860) > 0.$$ Koska funktio $A'$ on jatkuva, on sillä Bolzanon lauseen mukaan ainakin yksi nollakohta välillä $\pa 0{,}860, 0{,}864\pe$. Tämän nollakohdan kaksidesimaalinen likiarvo on $0{,}86$.
- Funktion suurin arvo löytyy derivaatan nollakohdasta tai välin päätepisteistä. Koska $A(0) = 0$, $A(0{,}86) \approx 1{,}1$ ja $A\left(\frac{\pi}{2}\right) = 0$, pinta-alan suurin arvo on noin $1{,}1$.
Olkoot \begin{align*} \va &= (\cos \varphi - 2\sin\varphi)\vi + \vj + (\sin \varphi + 2\cos\varphi)\vk,\\ \vb &= (\cos \varphi + \sin\varphi)\vi + \vj + (\sin \varphi - \cos\varphi)\vk \end{align*}
- Osoita, että vektorit $\va$ ja $\vb$ ovat kohtisuorassa toisiaan vastaan kaikilla $\varphi \in \R$.
- Olkoon $\varphi = 0$. Onko olemassa sellaisia kertoimia $s$, $t \in \R$, että $\vi - \vj = s\va + t\vb$?
[Pitkä S2012/9]
Vastaus
Ratkaisu löytyy täältä tehtävän 9 kohdalta.
Määritä funktion $$ f(x) = 3\cos^2\! x - \sin^2\! x - 2 $$ nollakohdat sekä suurin ja pienin arvo.
[Pitkä S2011/10]
Vastaus
Funktion lauseke sievenee muotoon $$f(x) = 4\cos^2 - 3.$$ Koska $0 \leq \cos^2\! x \leq 1$ kaikilla kulmilla $x$, voidaan päätellä, että funktion $f$ suurin arvo on $4-3 = 1$ ja pienin arvo $0 - 3 = -3$.
Funktion $f$ nollakohdat ovat $$ \pm \frac{\pi}{6} + n\cdot 2\pi $$ ja $$ \pm \frac{5\pi}{6} + n\cdot 2\pi, $$ missä $n$ on kokonaisluku.
- Derivoi funktio $g(x) = x\sin x$.
- Olkoon $f(x) = \sin x \cos x$. Laske derivaatta $f'(0)$.
- Laske funktion $$ f(x) = \frac{2 + \sin x}{2 + \cos x} $$ derivaatta pisteessä $x = \frac{\pi}{2}$.
[Pitkä K2010/2b & S2007/2a & K2008/3b]
Vastaus
- $\mathop{\mathrm{D}} (x\sin x) = x\cos x + \sin x$
- $f'(0) = 1$
- $f'\left(\dfrac{\pi}{2}\right) = \dfrac{3}{4}$
Tutki, kuinka monta juurta yhtälöllä $$ 3\tan x - 1 = 4x $$ on välillä $\pa -\pi/2, \pi/2\pe$.
[Pitkä K2010/9]
Vastaus
Funktion $$f(x) = 3\tan x - 4x - 1$$ derivaattafunktio on $$f'(x) = 3\tan^2\! x - 1.$$ Selvitetään derivaattafunktion nollakohdat välillä $\pa -\pi/2, \pi/2\pe$. Ne ovat $$ x = \pm \frac{\pi}{6}. $$ Laaditaan funktion $f$ kulkukaavio, josta nähdään, että funktio on aidosti kasvava väleillä $\left]-\frac{\pi}{2}, -\frac{\pi}{6}\right]$ ja $\left[\frac{\pi}{6}, \frac{\pi}{2}\right[$ ja aidosti vähenevä välillä $\left[-\frac{\pi}{6}, \frac{\pi}{6}\right]$. Koska lisäksi $f\left(-\frac{\pi}{6}\right) < 0$, funktiolla $f$ ei ole nollakohtaa välillä $\left]-\frac{\pi}{2}, \frac{\pi}{6}\right]$. Toisaalta koska $f\left(\frac{\pi}{6}\right) < 0$ ja $f\left(\frac{\pi}{3}\right) > 0$, on funktiolla $f$ tasan yksi nollakohta välillä $\left]\frac{\pi}{6}, \frac{\pi}{2}\right[$.
Tarkastellaan lauseketta $$ L(x) = \frac{\tan x - \sqrt{3}}{x - \frac{\pi}{3}}. $$
- Laske lauseketta muokkaamatta sille laskimella likiarvo, kun $x = \frac{\pi}{3} + 10^{-3n}$, missä $n$ saa arvot 1, 2, 3, 4 ja 5.
- Määritä $$ \lim_{x\rightarrow \pi/3} L(X) $$ tulkitsemalla lauseke sopivan funktion erotusosamääräksi. Mitä voidaan sanoa a-kohdassa lasketuista likiarvoista?
[Pitkä S2005/13]
Vastaus
Ratkaisu löytyy täältä tehtävän 13 kohdalta.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

