Kisallioppiminen.fi Logo

beta kisallioppiminen.fi MAA5 - Analyyttinen geometria

$\def\vi{\bar{\imath}} \def\vj{\bar{\jmath}} \def\vv{\bar{v}} \def\vu{\bar{u}} \def\vw{\bar{w}} \def\va{\bar{a}} \def\vb{\bar{b}} \def\vc{\bar{c}} \def\vk{\bar{k}} \def\vn{\bar{n}} \def\pv{\overline} \def\R{\mathbb{R}} \def\Q{\mathbb{Q}} \def\N{\mathbb{N}} \def\Z{\mathbb{Z}} \def\pa{\mathopen]} \def\pe{\mathclose[} \def\lb{\mathop{\mathrm{lb}}} \require{color} \newcommand\T{\Rule{0pt}{1em}{.3em}} $

Paraabeli ja muita pistejoukkoja

Tämän luvun tavoitteena on, että syvennät edellisissä luvuissa käsiteltyjen asioiden osaamista ja sovellat oppimaasi muihin yhtälön avulla määriteltyihin pistejoukkoihin. Osaat

  • käyttää paraabeliin liittyviä käsitteitä polttopiste, johtosuora, akseli ja huippu
  • muodostaa paraabelin yhtälön, jos paraabelin akseli on koordinaattiakselien suuntainen
  • piirtää koordinaatistoon suoran, ympyrän ja paraabelin lisäksi muitakin yhtälön avulla määriteltyjä pistejoukkoja
  • tutkia, kuuluuko annettu piste pistejoukkoon, jonka yhtälö tunnetaan.

Kurssissa MAA2 tutustuttiin toisen asteen polynomifunktioihin. Niiden kuvaajat ovat aina ylöspäin tai alaspäin aukeavia paraabeleja. Alla on esimerkiksi näkyvissä funktion $\,f(x) = x^2 - 2x - 3 \,$ kuvaaja.

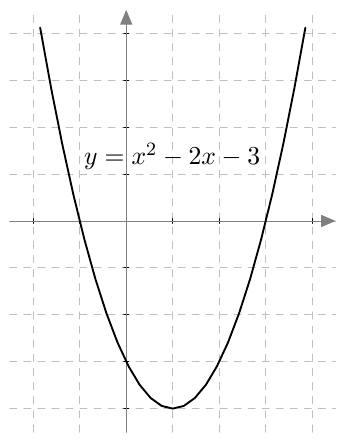
Ylöspäin ja alaspäin aukeavien paraabelien lisäksi on olemassa muihin suuntiin aukeavia paraabeleja. Yleisesti paraabeli määritellään etäisyyden avulla seuraavasti:

MÄÄRITELMÄ: PARAABELI

Kurssissa MAA2 tutustuttiin toisen asteen polynomifunktioihin. Niiden kuvaajat ovat aina ylöspäin tai alaspäin aukeavia paraabeleja. Alla on esimerkiksi näkyvissä funktion $\,f(x) = x^2 - 2x - 3 \,$ kuvaaja.

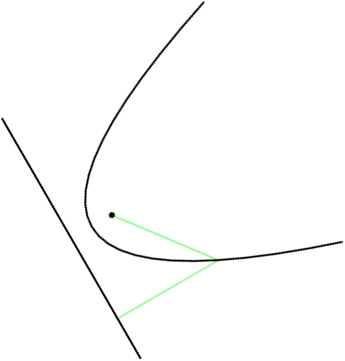
Alla on näkyvissä funktion $g(x) = -0{,}25x^2 + 2$ kuvaaja. Se on paraabeli, jonka johtosuora on $y = 3$ ja polttopiste $(0,1)$. Siniset janat havainnollistavat etäisyyksiä paraabelin pisteistä polttopisteeseen ja johtosuoraan:

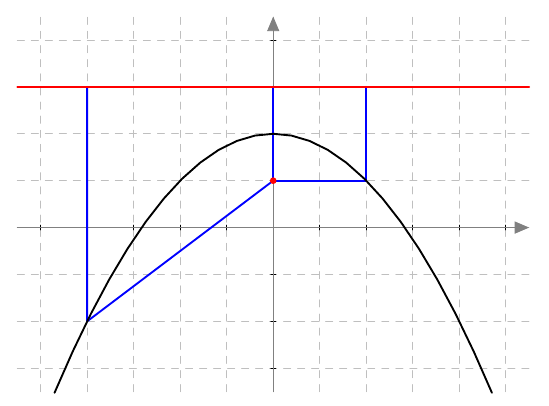
Piste $(0,2)$ on tämän paraabelin huippu ja $y$-akseli on tässä tapauksessa paraabelin akseli. Nämä MAA2-kurssista tutut käsitteet voidaan määritellä paraabelin polttopisteen ja johtosuoran avulla seuraavasti:

MÄÄRITELMÄ: PARAABELIN AKSELI JA HUIPPU

Paraabelin akseli on paraabelin johtosuoran se normaali, joka kulkee paraabelin polttopisteen kautta. Akselin ja paraabelin leikkauspiste on paraabelin huippu.
Piste $(0,2)$ on tämän paraabelin huippu ja $y$-akseli on tässä tapauksessa paraabelin akseli. Nämä MAA2-kurssista tutut käsitteet voidaan määritellä paraabelin polttopisteen ja johtosuoran avulla seuraavasti:

Paraabelille voidaan johtaa yhtälö, jos polttopiste ja johtosuora tunnetaan. Tarkastellaan esimerkiksi paraabelia, jonka polttopiste on $(4,0)$ ja johtosuora on $x = -2$. Pisteen $(x,y)$ etäisyys polttopisteestä on $$\sqrt{(x-4)^2 + y^2}$$ ja etäisyys johtosuorasta on $$\left| x-(-2)\right| = \left| x+2\right|.$$ 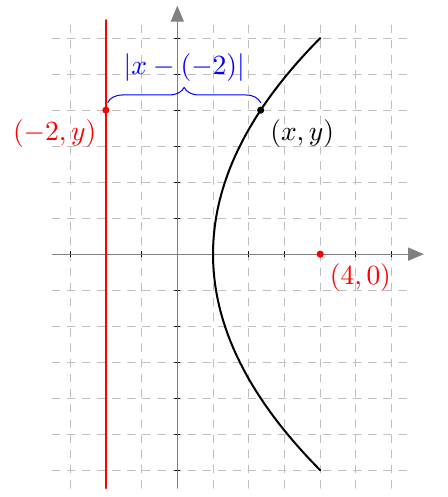Piste $(x,y)$ on paraabelin piste, jos ja vain jos sen etäisyydet polttopisteeseen ja johtosuoraan ovat yhtä suuret eli yhtälö $$ \sqrt{(x-4)^2 + y^2} = \left| x+2\right| \tag{A} $$ toteutuu.

Yhtälön (A) vasen ja oikea puoli ovat yhtä suuret, ja yhtäsuuruus säilyy toiseen potenssiin korotuksessa. Näin saadaan yhtälö $$ (x-4)^2 + y^2 = (x + 2)^2. \tag{B} $$ Yhtälöstä (B) päästään takaisin yhtälöön (A) ottamalla molemmilta puolilta neliöjuuri. Se on sallittua, koska yhtälön (B) kumpikin puoli on epänegatiivinen. Lisäksi käytetään tietoa, että $$\sqrt{(x+2)^2} = \left| x+2\right|.$$ Yhtälöt (A) ja (B) ovat siis yhtäpitäviä, eli ne toteutuvat täsmälleen samoilla muuttujien $x$ ja $y$ arvoilla.

Yhtälöstä (B) voidaan ratkaista $x$: \begin{align*} (x-4)^2 + y^2 &= (x + 2)^2 \\ x^2 - 8x + 16 + y^2 &= x^2 + 4x + 4 \\ y^2 &= 12x - 12 \\ 12x - 12 &= y^2 \\ 12x &= y^2 + 12 \\ x &= \frac{1}{12}y^2 + 1. \end{align*}

Mille tahansa paraabelille, jonka johtosuora on $x$- tai $y$-akselin suuntainen, voidaan johtaa yhtälö samaan tapaan kuin edellä tehtiin. Tällä tavalla voitaisiin todistaa oikeaksi myös seuraava teoreema:

TEOREEMA

Jos paraabelin akseli on $y$-akselin suuntainen, niin paraabelin yhtälö on muotoa $$y = ax^2 + bx + c,$$ missä $a\neq 0$. Paraabeli aukeaa

  • ylöspäin, jos $a > 0$
  • alaspäin, jos $a < 0$.

Jos paraabelin akseli on $x$-akselin suuntainen, niin paraabelin yhtälö on muotoa $$x = ay^2 + by + c,$$ missä $a\neq 0$. Paraabeli aukeaa

  • oikealle, jos $a > 0$
  • vasemmalle, jos $a < 0$.

Missä pisteissä seuraavat paraabelit leikkaavat koordinaattiakselit? Päättele lisäksi paraabelien aukeamissuunta sekä huipun koordinaatit. Muista, että voit tarkistaa vastauksesi piirtämällä paraabelin laskimella tai tietokoneella.

  1. $x = 4(y-3)(y + 2)$
  2. $y = 3x^2 + 18x + 25$
  3. $y = 3(x+1)(1-x)$
  4. $x = 1 - 8y - 4y^2$

Seuraavassa tehtävässä harjoitellaan paraabelin yhtälön muodostamista. Tavoitteena on muodostaa yhtälö ja saattaa se teoreeman 16 mukaiseen muotoon.

Tehtävänä on muodostaa yhtälö paraabelille, jonka polttopiste on $(0,3)$ ja johtosuora on $y = -1$.

  1. Piirrä paraabelin polttopiste ja johtosuora koordinaatistoon. Merkitse kuvaan pisteitä, jotka ovat yhtä kaukana polttopisteestä ja johtosuorasta. Mihin suuntaan paraabeli aukeaa?
  2. Muodosta lauseke, joka ilmaisee pisteen $(x,y)$ etäisyyden pisteestä $(0,3)$.
    Vinkki: kertaa tarvittaessa teoreema 5 luvusta Etäisyys.
  3. Muodosta lauseke, joka ilmaisee pisteen $(x,y)$ etäisyyden suorasta $y = -1$.
    Vinkki: Voit päätellä samaan tapaan kuin edellisessä esimerkissä tehtiin tai käyttää luvun Suora teoreemaa 13.
  4. Muodosta edellisten kohtien lausekkeista yhtälö, jonka mukaan pisteen $(x,y)$ etäisyys polttopisteestä $(0,3)$ on yhtä suuri kuin pisteen $(x,y)$ etäisyys johtosuorasta $y = -1$.
  5. Ratkaise muodostamasi yhtälöstä $y$.
    Vinkki: aloita korottamalla yhtälön kumpikin puoli toiseen potenssiin.

  5. $y = \frac{1}{8}x^2 + 1$

Paraabelin yhtälö voidaan muodostaa myös tilanteessa, jossa tunnetaan paraabelin kolme pistettä. Esimerkiksi alla olevasta kuvasta nähdään, että paraabeli kulkee pisteiden $(-1,2)$, $(3,1)$ ja $(4,4)$ kautta.

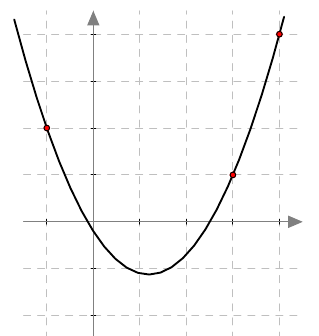
Ylöspäin aukeavan paraabelin yhtälö on muotoa $y = ax^2 + bx + c$. Edellä mainitut kolme pistettä toteuttavat tämä yhtälön, joten saadaan yhtälöryhmä $$ \left\{\begin{aligned} 2 &= a\cdot (-1)^2 + b \cdot (-1) + c \\ 1 &= a\cdot 3^2 + b \cdot 3 + c \\ 4 &= a\cdot 4^2 + b \cdot 4 + c. \end{aligned}\right. $$ Tämä yhtälöryhmä voidaan kirjoittaa myös muodossa $$ \left\{\begin{aligned} a - \phantom{4}b + c &= 2 \\ 9a + 3b + c &= 1 \\ 16a + 4b + c &= 4. \end{aligned}\right. $$ Kun se ratkaistaan käsin tai koneella kuten kurssilla MAA4, saadaan ratkaisuksi $$ \left\{\begin{aligned} a &= 0{,}65 \\ b &= -1{,}55 \\ c &= -0{,}2. \end{aligned}\right. $$ Paraabelin yhtälö on siis $y = 0{,}65x^2 - 1{,}55x - 0{,}2$.

Alaspäin aukeava paraabeli kulkee pisteiden $(0,1)$, $(1,-1)$ ja $(-2,-1)$ kautta. Määritä paraabelin yhtälö.

$y = -x^2 - x + 1$

Suoran yhtälö, ympyrän yhtälö ja paraabelin yhtälö ovat kaikki esimerkkejä pistejoukon yhtälöstä. Esimerkiksi ne pisteet, jotka toteuttavat yhtälön $y = 1{,}5x - 2$, muodostavat koordinaatistoon suoran.

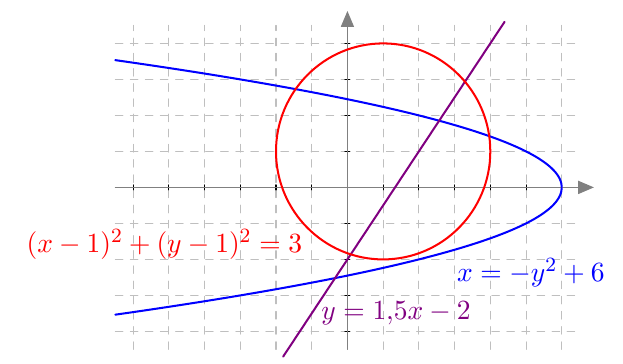
Ylla olevaan kuvaan on merkitty myös ne pisteet, jotka toteuttavat yhtälön $(x-1)^2 + (y-1)^2 = 3$, sekä ne pisteet, jotka toteuttavat yhtälön $x = -y^2 + 6$.

Yleisesti tason pistejoukon yhtälö määritellään seuraavasti:

MÄÄRITELMÄ: PISTEJOUKON YHTÄLÖ

Tason pistejoukon yhtälö on muuttujien $x$ ja $y$ yhtälö, jolla on seuraava ominaisuus:
Piste $(x,y)$ kuuluu pistejoukkoon, jos ja vain jos pisteen $(x,y)$ koordinaatit toteuttavat yhtälön.

Tietokoneen avulla voidaan piirtää esimerkiksi niiden pisteiden joukko, jotka toteuttavat yhtälön $$x^4 + 2x^2y^2 + y^4 - x^3 + 3xy^2 = 0.$$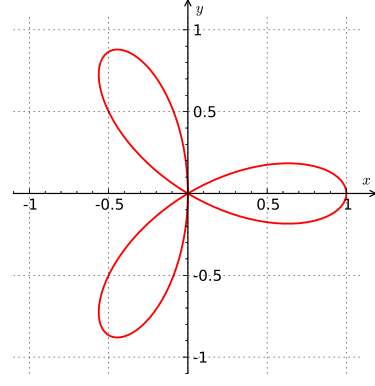

Kuva: Krishnavedala (Oma teos) [CC BY-SA 3.0], lähde: Wikimedia Commons.

Tämä pistejoukko on nimeltään kolmen lehden ruusu (englanniksi myös kolmilehtinen apila: three-leaved clover).

Tehtävänä on piirtää pistejoukko, jonka yhtälö on $(x-y)(x+2) = 0$.

  1. Hajota pistejoukon yhtälö MAA2-kurssista tutun tulon nollasäännön avulla kahdeksi yhtälöksi.
  2. Piirrä koordinaatistoon niiden pisteiden joukko, jotka toteuttavat yhtälön $y = x$.
  3. Piirrä koordinaatistoon niiden pisteiden joukko, jotka toteuttavat yhtälön $x = -2$.
  4. Mitkä koordinaatiston pisteet toteuttavat yhtälön $(x-y)(x+2) = 0$?

Joskus halutaan tutkia, kuuluuko yksittäinen piste johonkin pistejoukkoon. Tämä voidaan tehdä sijoittamalla pisteen koordinaatit yhtälön eri puolille ja katsomalla, toteutuuko yhtälö.

Tarkastellaan esimerkiksi pistejoukkoa, jonka yhtälö on $$x^3 + y^3 = 3xy.$$ Tämän pistejoukon nimi on Cartesiuksen lehti. Se on nimetty ranskalaisen matemaatikon René Descartesin mukaan.

Tutkitaan, kuuluuko piste $(-2,1)$ tähän pistejoukkoon. Sijoitetaan pisteen koordinaatit Cartesiuksen lehden yhtälön vasemmalle puolelle: $$x^3 + y^3 = (-2)^3 + 1^3 = -8 + 1 = -7.$$ Sijoitetaan pisteen koordinaatit yhtälön oikealle puolelle: $$3xy = 3\cdot (-2) \cdot 1 = -6.$$ Yhtälön vasen ja oikea puoli ovat eri suuret, joten piste $(-2,1)$ ei toteuta Cartesiuksen lehden yhtälöä.

Tutkitaan pistejoukkoa, jonka yhtälö on $$(x^2 + y^2 + 25)^2 - 100x^2 = 625.$$ Kuuluvatko seuraavat pisteet tähän pistejoukkoon?

  1. $(1,-1)$
  2. $(6,2)$
  3. $(-7,0)$

  1. Ei.
  2. Kyllä.
  3. Ei.

Paraabelin yhtälö

Muodosta yhtälö paraabelille, jonka polttopiste on $(0,1)$ ja jonka johtosuora on $y = -1$.

$y = \frac{1}{4}x^2$

Paraabeli

Osoita, että suora $2ax - y - a^2 = 0$ sivuaa paraabelia $y = x^2$ vakion $a$ kaikilla arvoilla.

Tarkastele suoran ja paraabelin leikkauspisteiden lukumäärää. Onko suora jollakin vakion $a$ arvolla yhdensuuntainen paraabelin akselin kanssa?

Paraabeli

Etsi suoran $x - y = 1$ ja paraabelin $y = x^2 - 3$ leikkauspisteet.

Leikkauspisteet ovat $(-1,-2)\ $ ja $\ (2,1)$.

Paraabeli

Paraabeli kulkee pisteiden $(5,8)$, $(13,8)$ ja $(7,-4)$ kautta. Määritä paraabelin yhtälö.
Vinkki: aloita esimerkiksi hahmottelemalla pisteet koordinaatistoon ja päättelemällä, mihin suuntaan paraabeli aukeaa.

$y = x^2 - 18x + 73$

Paraabeli

Maantiellä on tunneli, jonka aukko on alaspäin aukeavan paraabelin muotoinen. Aukon korkeus on 5,0 m ja leveys 10 m. Erikoiskuljetuksen leveys on 5,5 metriä ja korkeus 4,2 m. Mahtuuko kuljetus tunnelista?

Ei mahdu. Tunnelista mahtuvan 5,5 metriä leveän kuljetuksen maksimikorkeus on alle 4 metriä. (Tunnelin aukkoa vastaavan paraabelin yhtälö on $y = -0{,}2x^2 + 5$.)

Paraabeli

Osoita, että paraabelit $y = x^2 + ax + a$ kulkevat vakio $a$ arvosta riippumatta saman pisteen kautta. Mikä tämä piste on?

Piste on $(-1,1)$.
Voit selvittää leikkauspisteen valitsemalla vakiolle $a$ kaksi eri arvoa ja tutkimalla, missä pisteessä nämä paraabelit leikkaavat. Sen jälkeen pitää vielä näyttää, että paraabelit kulkevat tämän pisteen kautta vakion $a$ arvosta riippumatta.

Paraabeli

Määritä paraabelin $y = -x^2 + 5$ pisteet, joiden etäisyys origosta on $7$.

Pisteet ovat $\ (\sqrt{3}, 2)$, $\ (-\sqrt{3}, 2)$, $\ (\sqrt{6}, -1)\ $ ja $\ (-\sqrt{6}, -1)$.

Paraabeli

Tarkastellaan paraabelia $y = x^2$. Tehtävänä on muodostaa yhtälö sille tämän paraabelin tangentille, joka on suoran $y = 3x$ suuntainen.

  1. Mitä muotoa ovat sellaisten suorien yhtälöt, jotka ovat yhdensuuntaisia suoran $y = 3x$ kanssa?
  2. Kuinka monta yhteistä pistettä paraabelilla ja sen tangetilla on?
  3. Muodosta a- ja b-kohtien avulla sopiva yhtälö ja ratkaise se.
  4. Mikä on etsityn tangentin yhtälö? Missä pisteessä se sivuaa paraabelia $y = x^2$?

  1. $y = 3x + h$
  2. Niillä on yksi yhteinen piste.
  3. Yhtälöllä $x^2 - 3x - h = 0$ on tasan yksi ratkaisu, jos ja vain jos sen diskriminantti on nolla eli $9+4h = 0$.
  4. $y= 3x - \frac{9}{4}$, sivuamispiste $\left(\frac{3}{2}, \frac{9}{4}\right)$.

Paraabeli

Paraabelin polttopiste on $(0,b)$ ja johtosuoran yhtälö on $y = -b$. Muodosta paraabelin yhtälö.

$y = \dfrac{1}{4b}x^2$

Paraabeli

Voit hyödyntää tässä tehtävässä tehtävän 4.10 tulosta.

  1. Muodosta yhtälö paraabelille, jonka polttopiste on $\left(0, \frac{1}{4}\right)$ ja johtosuora on $y = -\frac{1}{4}$.
  2. Määritä paraabelin $y = -\frac{1}{3}x^2$ polttopiste ja johtosuora.

  1. $y = x^2$
  2. Polttopiste on $\left(0, -\frac{3}{4}\right)$ ja johtosuora $y = \frac{3}{4}$.

Pistejoukon yhtälö

Piirrä koordinaatistoon pistejoukko, jonka yhtälö on

  1. $(2x+y)(x-y-1)$
  2. $y^2 = 4$
  3. $y^2 - x^2 = 0$

  1. Suorat $y = -2x$ ja $y = x-1$.
  2. Suorat $y = 2$ ja $y = -2$.
  3. Suorat $y = x$ ja $y = -x$.

Pistejoukon yhtälö

Yhtälö $x^2 + 2y^2 + 4xy - 3x + 5y + 2 = 0$ määrittelee pistejoukon, joka on tyypiltään hyperbeli.

  1. Määritä ne pisteet, joissa tämä hyperbeli leikkaa koordinaattiakselit.
  2. Piirrä tämä hyperbeli laskimen tai tietokoneen avulla.

  1. Pisteissä $\ (1,0)$, $\ (2,0)$, $\ \left(0, -\frac{1}{2}\right)\ $ ja $\ (0,-2)$.

Pistejoukon yhtälö

Päättele, millaisen pistejoukon seuraavat yhtälöt määrittelevät. Tarkista piirtämällä pistejoukot koordinaatistoon laskimella tai tietokoneella.

  1. $4x^2 - y = 0$
  2. $4 - x^2 - y^2 = 0$
  3. $4x - y^2 = 0$
  4. $4x^2 - y^2 = 0$

  1. Ylöspäin aukeava paraabeli.
  2. Ympyrä, jonka keskipiste on origo ja säde on $2$.
  3. Oikealle aukeava paraabeli.
  4. Suorat $y = 2x$ ja $y = -2x$.

Pistejoukon yhtälö

Tutkitaan pistejoukkoa, jonka pisteillä on seuraava ominaisuus: Pisteen etäisyys pisteestä $(0,4)$ on kaksi kertaa niin suuri kuin etäisyys suorasta $y = 1$.

  1. Muodosta pistejoukon yhtälö.
  2. Piirrä pistejoukko koordinaatistoon laskimella tai tietokoneella a-kohdan yhtälön avulla.
  3. Mikä on syntyneen käyrän nimi? Kurkista esimerkiksi tänne. Muistatko tai osaatko päätellä vastaavat suomenkieliset nimitykset?

  1. $x^2 - 3y^2 + 12 = 0$
  3. Käyrä on hyperbeli.

Pistejoukon yhtälö

Tutkitaan pistejoukkoa, jonka pisteillä on seuraava ominaisuus: Pisteen etäisyys suorasta $y = 4$ on kaksi kertaa niin suuri kuin etäisyys pisteestä $(0,1)$.

  1. Muodosta pistejoukon yhtälö.
  2. Piirrä pistejoukko koordinaatistoon laskimella tai tietokoneella a-kohdan yhtälön avulla.
  3. Mikä on syntyneen käyrän nimi? Kurkista esimerkiksi tänne. Muistatko tai osaatko päätellä vastaavat suomenkieliset nimitykset?

  1. $4x^2 + 3y^2 - 12 = 0$
  3. Käyrä on ellipsi.

Pistejoukon yhtälö

Ympyrät kulkevat origon kautta ja sivuavat suoraa $y = -6$. Tehtävänä on selvittää, minkä käyrän tällaisten ympyröiden keskipisteet muodostavat.

  1. Piirrä koordinaatistoon suora $y = -6$. Hahmottele kuvaan muutama ympyrä, joka sivuaa tätä suoraa ja kulkee origon kautta.
  2. Tarkastele ympyrän keskipisteen etäisyyttä suorasta $y = -6$ ja origosta. Mitä voit päätellä näistä etäisyyksistä? Muodosta yhtälö ja muokkaa se mahdollisimman selkeään muotoon.
  3. Piirrä b-kohdan yhtälöä vastaava pistejoukko koordinaatistoon. Mikä käyrä on kysymyksessä?

  3. Paraabeli $y = \frac{1}{12}x^2 - 3$

Pistejoukon yhtälö

Tarkastellaan pistejoukkoa, jonka yhtälö on $xy = 2$.

  1. Piirrä tämä pistejoukko koordinaatistoon laskimen tai tietokoneen avulla. Mikä käyrä on kysymyksessä? Kurkista esimerkiksi tänne. Muistatko tai osaatko päätellä vastaavat suomenkieliset nimitykset?
  2. Määritä ne vakion $b$ arvot, joilla suora $y = -2x + b$ ei leikkaa tarkasteltavaa pistejoukkoa. Tarkista vastauksesi järkevyys vertaamalla sitä piirtämääsi kuvaan.

  1. Käyrä on hyperbeli.
  2. $-4 < b < 4$

Pistejoukon yhtälö

Jana, jonka pituus on $6$, liikuu ympyrän $(x+3)^2 + (y-1)^2 = 16$ sisällä niin, että janan päätepisteet ovat koko ajan ympyrän kehällä. Minkä käyrän janan keskipiste piirtää?
Vinkki: Piirrä tilanteesta kuva. Pystytkö määrittämään janan keskipisteen etäisyyden ympyrän keskipisteestä?

Ympyrän $(x+3)^2 + (y-1)^2 = 7$.

Tasokäyrä $K$ muodostuu niistä pisteistä $(x,y)$, joiden etäisyys origosta on yhtä suuri kuin etäisyys suorasta $y = 2$. Johda käyrän yhtälölle muoto $y = f(x)$.
[Pitkä S2016/7a]

$y = -\frac{1}{4}x^2 + 1$

Tasokäyrä kulkee pisteen $(3,4)$ kautta. Määritä käyrän yhtälö, kun kyseessä on

  1. origon kautta kulkeva suora
  2. origokeskinen ympyrä
  3. ylöspäin aukeava paraabeli, jonka huippu on origossa.

[Pitkä S2015/2]

  1. Ratkaistussa muodossa $y = \frac{4}{3}x$ tai normaalimuodossa $4x - 3y = 0$.
  2. $x^2 + y^2 = 25$
  3. $y = \frac{4}{9}x^2$

  1. Missä pisteessä paraabelit $y = x^2 + x + 1$ ja $y = x^2 + 2x + 3$ leikkaavat?
  2. Määritä käyrien $y = 12x^3 - 36x$ ja $y = -12x^2 + 36x$ leikkauspisteet.

[Pitkä S2014/1b & K2013/8a]

  1. Pisteessä $(-2,3)$.
  2. Leikkauspisteet ovat $\ (-3,-216)$, $\ (0,0) \ $ ja $\ (2,24)$.

Paraabelin $y = x^2$ jokaista pistettä siirretään vektorin $\vv$ verran. Määritä näin syntyvän käyrän yhtälö muodossa $y = f(x)$, kun

  1. $\vv = 2\vj$
  2. $\vv = 3\vi$
  3. $\vv = 3\vi + 2\vj$.

[Pitkä S2014/4]

  1. $y = x^2 + 2$
  2. $y = (x-3)^2$ eli $y = x^2 - 6x + 9$
  3. $y = (x-3)^2 + 2$ eli $y = x^2 - 6x + 11$.

Tarkastellaan tasokäyrää, jonka yhtälö on $2x^2 + 2y^2 - 3xy - 2x + 2y - 4 = 0$.

  1. Määritä käyrän ja koordinaattiakselien leikkauspisteet.
  2. Osoita, että kaikki leikkauspisteet ovat saman ympyrän kehällä, ja määritä tämän ympyrän yhtälö.
  3. Suora kulkee origon ja b-kohdan ympyrän keskipisteen kautta. Missä pisteissä tämä suora leikkaa alkuperäisen käyrän?

[Pitkä S2013/14]

  1. Leikkauspisteet ovat $\ (-1,0)$, $\ (2,0)$, $\ (0,-2)\ $ ja $\ (0,1)$.
  2. Ympyrän yhtälö on $\left(x - \frac{1}{2} \right)^2 + \left(y + \frac{1}{2} \right)^2 = \frac{10}{4}$.
  3. Leikkauspisteet ovat $\left(\frac{2-4\sqrt{2}}{7}, \frac{-2+4\sqrt{2}}{7}\right)$ ja $\left(\frac{2+4\sqrt{2}}{7}, \frac{-2-4\sqrt{2}}{7}\right)$.

Funktion $f(x) = ax^2 + bx + c$ kuvaaja kulkee pisteiden $\ (-1,12)$, $\ (0,5)\ $ ja $\ (2,-3)\ $ kautta. Määritä lausekkeen $a + b + c$ arvo.
[Pitkä S2010/4]

$a + b + c = 0$

Tarkastellaan origon kautta kulkevaa ympyrää, jonka keskipiste on positiivisella $y$-akselilla. Kuinka suuri tällaisen ympyrän säde voi enintään olla, jotta origo on ympyrän ja paraabelin $y = x^2$ ainoa yhteinen piste?

Ympyrän säde voi olla enintään $\frac{1}{2}$.

Paraabeli $y = x^2$ erottaa suoran $y = 2x$ suuntaisista suorista janoja. Osoita, että kaikkien tällaisten janojen keskipisteet ovat samalla suoralla. Mikä tämän suoran yhtälö on?
Vinkki: teoreema 6.

Suoran yhtälö on $x = 1$.

Tasamaalla sijaitsevalta räjäytystyömaalta lentää kivi 72 metrin päähän. Kivi katkaisee 48 metrin päässä olevan ohuen puun 13,5 metrin korkeudelta. Oletetaan, että kiven lentorata on paraabeli. Kuinka korkealla kivi käy?
[Pitkä S1998/4]

Kivi käy 15 metrin korkeudessa.

Kahden metrin korkeudelta heitetty pallo osuu viiden metrin päässä olevan puun runkoon viiden metrin korkeudella. Pallon lentoratana on paraabeli, jonka huippu on heittäjän ja puun välissä kahden metrin etäisyydellä puusta. Laske heittokulma. Anna vastaus asteen kymmenesosan tarkkuudella.
[Pitkä K1991/6]

Heittokulma on noin $74{,}5^\circ$.
Vinkkejä: Sijoita paraabeli koordinaatistoon niin, että sen huippu on $y$-akselilla. Mitä muotoa sen yhtälö silloin on? Muodosta yhtälö tangentille, joka kulkee heittopisteen kautta. Muista, että paraabelilla ja sen tangentilla on vain yksi yhteinen piste. Selvitä tämän tiedon avulla tangentin kulmakerroin.

Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.