Kombinatoriikkaa
Luvun tavoitteet
Tämän luvun tavoitteena on, että ... Osaat
Tuloperiaate – peräkkäiset valinnat
Tässä luvussa opitaan erilaisia tapoja lukumäärien laskemiseen. Näistä tavoista monet pohjautuvat niin sanottuun tuloperiaatteeseen. Sitä voidaan soveltaa tilanteissa, joissa kokonaisuus muodostetaan tekemällä peräkkäisiä valintoja. Seuraavat tehtävät havainnollistavat asiaa.
Tuloperiaate
Tilausravintolan ruokalistalla on neljä alkuruokaa, kolme pääruokaa ja kaksi jälkiruokaa. Kuinka monta erilaista ateriakokonaisuutta on mahdollista muodostaa, jos asiakas valitsee
- alkuruoan ja pääruoan
- pääruoan ja jälkiruoan
- kaikki kolme ruokalajia?
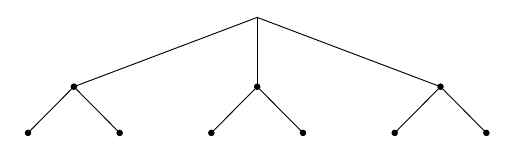
Mihin kohtaan alla oleva kuva sopii havainnollistukseksi?
VASTAUS
- Vaihtoehtoja on $4 \cdot 3 = 12$. Alkuruoka voidaan valita neljällä erilaisella tavalla. Valittiinpa se miten tahansa, voidaan pääruoka valita sen jälkeen kolmella erilaisella tavalla. Jokaiseen alkuruokaan liittyy siis kolme erilaista pääruokamahdollisuutta.
- Vaihtoehtoja on $3 \cdot 2 = 6$.
- Vaihtoehtoja on $4 \cdot 3 \cdot 2 = 24$.
Kuva sopii havainnollistukseksi b-kohtaan, jossa ensin valitaan pääruoka kolmesta vaihtoehdosta ja sen jälkeen kaikissa tapauksissa jälkiruoka voidaan vielä valita kahdesta vaihtoehdosta. Erilaisia yhdistelmiä on yhtä monta kuin kuvassa alimmalla rivillä on mustia pisteitä eli $3 \cdot 2 = 6$ kappaletta.
Tuloperiaate
Olohuoneessa on kattolamppu, jalkalamppu ja ikkunalaudalla pöytälamppu. Tehtävänä on selvittää, kuinka monella erilaisella tavalla olohuoneen voi näiden avulla valaista.
- Miten alla oleva kaavio liittyy asiaan?
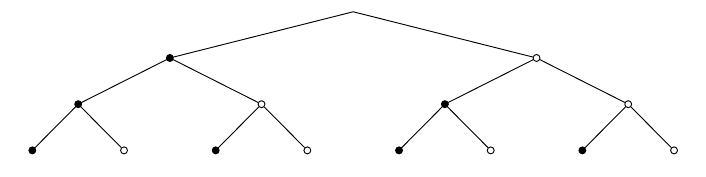
- Kuinka monella tavalla olohuoneen voi valaista näiden kolmen lampun avulla?
VASTAUS
- Jokainen kolmesta lampusta voi olla toisistaan riippumatta päällä (valkoinen pompula) tai pois päältä (musta pompula). Kaavion ylin rivi kuvaa sitä, onko ensimmäinen lamppu päällä vai pois päältä. Vastaavasti keskimmäinen ja alin rivi kuvaavat sitä, ovatko toinen ja kolmas lamppu päällä vai pois päältä. Erilaiset yhdistelmät vastaavat kaavion haaroja. Esimerkiksi oikeanpuoleisin haara (kolme valkoista pompulaa) kuvaa tilannetta, jossa kaikki olohuoneen lamput ovat päällä.
- Kaavion avulla voidaan päätellä, että olohuoneen voi kolmen lampun avulla valaista $2 \cdot 2 \cdot 2 - 1 = 8 - 1 = 7$ eri tavalla. Huomaa, että kaavion vasen haara kuvaa tilannetta, jossa kaikki lamput ovat pois päältä, joten sitä ei voi laskea mukaan, koska kysytään, miten monella tavalla olohuoneen voi valaista.
Jos kokonaisuus voidaan muodostaa tekemällä peräkkäisiä valintoja, onnistuu eri vaihtoehtojen havainnollistaminen puukaavion avulla samaan tapaan kuin edellisissä tehtävissä. Esimerkiksi alla oleva kaavio kuvaa tilannetta, jossa ensimmäisessä vaiheessa on neljä vaihtoehtoa ja seuraavassa vaiheessa kolme vaihtoehtoa. Kaaviosta nähdään, että erilaisia kokonaisuuksia voidaan muodostaa kaikkiaan $4 \cdot 3 = 12$.
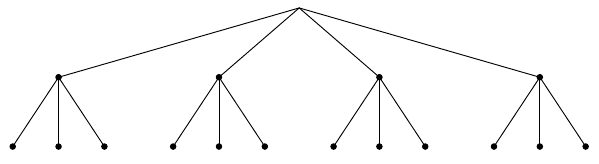
Päättelytapa voidaan yleistää kaikkiin samantyyppisiin tilanteisiin:
TEOREEMA
Oletetaan, että kokonaisuuden muodostaminen voidaan jakaa peräkkäisiin vaiheisiin, jotka eivät riipu toisistaan. Jos vaiheita on $k$ kappaletta, ja
$\phantom{AA}$ 1. vaiheessa on $n_1$ vaihtoehtoa
$\phantom{AA}$ 2. vaiheessa on $n_2$ vaihtoehtoa
$\phantom{AA}$ $\vdots$
$\phantom{AA}$ $k$. vaiheessa on $n_k$ vaihtoehtoa
niin kokonaisuus voidaan muodostaa $n_1 \cdot n_2 \cdot \dots \cdot n_k$ eri tavalla.
Seuraavissa tehtävissä harjoitellaan tuloperiaatteen soveltamista:
Tuloperiaate
Jokaiseen pankkikorttiin liittyy nelinumeroinen tunnusluku.
- Kuinka monta erilaista tunnuslukua on olemassa?
- Kuinka monessa tunnusluvussa mikään numero ei esiinny useammin kuin kerran?
- Kuinka monessa tunnusluvussa kaikki numerot ovat samoja?
VASTAUS
- Tunnusluku voidaan muodostaa valitsemalla sen numerot peräkkäin. Ensimmäiselle numerolle on 10 vaihtoehtoa (0-9), samoin seuraaville. Erilaisia tunnuslukuja on siis olemassa tuloperiaatteen nojalla $10 \cdot 10 \cdot 10 \cdot 10 = 10\,000$ kappaletta.
- Tunnusluvun ensimmäinen numero voi olla mikä tahansa numeroista 0-9, joten vaihtoehtoja on 10 kpl. Toinen numero ei voi olla sama kuin ensimmäinen, joten vaihtoehtoja on 9 kpl. Vastaavasti kolmas numero voidaan valita 8 eri tavalla ja neljäs 7 eri tavalla. Tunnuslukuja, joissa mikään numero ei esiinny useammin kuin kerran, on siis $10 \cdot 9 \cdot 8 \cdot 7 = 5\,040$ kappaletta.
- Tällaisia tunnuslukuja ovat 0000, 1111, 2222, $\ldots$, 9999. Niitä on 10 kappaletta.
Tuloperiaate
Suomen kielen aakkosissa on 29 kirjainta. Tarkastellaan kahden kirjaimen (etunimen ja sukunimen alkukirjain) yhdistelmiä.
- Kuinka monta erilaista nimikirjainten yhdistelmää suomen kielen aakkosista voidaan muodostaa?
- Kuinka monta osallistujaa tapahtumassa on oltava, jotta voidaan olla täysin varmoja, että ainakin kahdella osallistujalla on samat nimikirjaimet?
VASTAUS
- Etunimen alkukirjain voidaan valita 29 eri tavalla, samoin sukunimen alkukirjain. Erilaisia nimikirjainten yhdistelmiä on tuloperiaatteen nojalla $29 \cdot 29 = 841$ kappaletta.
- Osallistujia on oltava 842. Pahimmassa tapauksessa 841 osallistujalla on kaikilla eri nimikirjaimet. Jos osallistujia tulee yksi lisää, ei hänelle riitä enää eri nimikirjaimia a-kohdan nojalla, vaan hänellä on välttämättä samat nimikirjaimet kuin jollakin toisella osallistujalla.
Tuloperiaate
Tietojärjestelmän salasanalle asetetaan seuraavat vaatimukset:
- salasanassa on oltava kuusi merkkiä
- sallitut merkit ovat numerot 0-9 sekä erikoismerkit !, #, %, =, +, ?
- salasanan pitää sisältää ainakin yksi edellä mainituista kuudesta erikoismerkistä.
Tehtävänä on selvittää, kuinka monta erilaista salasanaa tällä tavalla on mahdollista muodostaa.
- Kuinka monta ehdot 1-2 täyttävää salasanaa on mahdollista muodostaa?
- Kuinka monta kuuden merkin mittaista salasanaa on mahdollista muodostaa pelkistä numeroista?
- Kuinka monta ehdot 1-3 täyttävää salasanaa on mahdollista muodostaa?
VASTAUS
- Salasanan jokainen merkki voidaan valita 16 eri tavalla, joten erilaisia salasanoja on $16^6 = 16\,777\,216$.
- Salasanan jokainen merkki voidaan valita 10 eri tavalla, joten erilaisia salasanoja on $10^6 = 1\,000\,000$.
- Ehdot 1-2 täyttäviä salasanoja on $16^6 = 16\,777\,216$. Pelkistä numeroista muodostettuja salasanoja on $10^6 = 1\,000\,000$. Salasanoja, joissa on ainakin yksi erikoismerkki, on $16^6 - 10^6 = 15\,777\,216$.
Järjestysten ja jonojen lukumäärät
Tuloperiaatteen avulla voidaan laskea erilaisten järjestysten lukumääriä. Esimerkiksi jos henkilöt A, B ja C järjestetään jonoksi, voidaan jonon ensimmäinen jäsen valita kolmella tavalla, seuraava kahdella tavalla ja jäljelle jääneestä henkilöstä tulee jonon viimeinen jäsen. Erilaisia järjestyksiä on siten $3 \cdot 2 \cdot 1 = 6$ kappaletta. Tässä esiintyvää peräkkäisten positiivisten kokonaislukujen tuloa sanotaan kertomaksi, kuten alla olevasta määritelmästä käy ilmi.
MÄÄRITELMÄ: KERTOMA
Olkoon $n$ positiivinen kokonaisluku. Luvun $n$ kertoma on kokonaislukujen $1, \ldots, n$ tulo: $$ n! = n \cdot (n-1) \cdots 2 \cdot 1 $$ Erikseen sovitaan, että luvun $0$ kertoma on yksi: $$0! = 1.$$
Luvun $n$ kertoma ilmaisee, miten monella tavalla $n$-alkioinen joukko voidaan järjestää jonoon. Tämä osoitetaan seuraavassa tehtävässä.
Järjestysten lukumäärä
Tarkastellaan joukkoa, jossa on $n$ alkiota. Tehtävänä on laskea, kuinka monella tavalla tämän joukon alkiot voidaan järjestää jonoon.
- Kuinka monella tavalla jonon ensimmäinen jäsen voidaan valita?
- Kuinka monella tavalla jonon toinen jäsen voidaan valita?
- Kuinka monella tavalla jonon kolmas jäsen voidaan valita?
- Miten vaihtoehtojen määrä muuttuu, kun jonon muodostaminen etenee?
- Kuinka monella tavalla jonon toiseksi viimeinen jäsen voidaan valita?
- Kuinka monella tavalla jonon viimeinen jäsen voidaan valita?
- Kuinka monta erilaista jonoa on mahdollista muodostaa?
VASTAUS
- Ensimmäinen jäsen voidaan valita $n$ eri tavalla.
- Toinen jäsen voidaan valita $n-1$ eri tavalla.
- Kolmas jäsen voidaan valita $n - 2$ eri tavalla.
- Tapoja valita jonon seuraava jäsen on aina yksi vähemmän.
- Toiseksi viimeinen jäsen voidaan valita $2$ eri tavalla.
- Viimeinen jäsen voidaan valita $1$ tavalla, koska vain yksi on enää jäljellä.
- Tuloperiaatteen nojalla erilaisia jonoja voidaan muodostaa $n \cdot (n-1) \cdot (n-2) \cdots 2 \cdot 1 = n!$ kappaletta.
Edellisen tehtävän tuloksesta saadaan seuraava teoreema:
TEOREEMA
Jos joukossa on $n$ alkiota, joukon alkiot voidaan järjestää jonoon $n!$ eri tavalla.
Perustelu tehtävässä 1.6.
Kertoma ilmaisee siis $n$-alkioisen joukon järjestysten eli niin sanottujen permutaatioiden lukumäärän. Esimerkiksi neljän alkion joukon $\{ a, b, c \}$ permutaatioita on kuusi erilaista, sillä $3! = 3\cdot 2 \cdot 1 = 6$. Ne voidaan luetella: \begin{align*} &abc, bca, cab \\ &acb, bac, cba \end{align*}
Järjestykset ja niiden lukumäärät
- Kuinka monta permutaatiota on joukolla $\{ a, b, c, d\}$?
- Luettele kaikki joukon $\{ a, b, c, d\}$ permutaatiot. Käytä jotain johdonmukaista menetelmää, jotta mikään ei jää huomaamatta eikä mikään tule useammin kuin kerran.
- Oletetaan, että yhden permutaation kirjoittaminen paperille kestää 2 sekuntia. Tutki kokeilemalla, mikä on suurin joukko, jonka kaikki permutaatiot on vielä jotenkin mielekästä kirjoittaa käsin näkyviin.
VASTAUS
- Permutaatioita on $4! = 4\cdot 3 \cdot 2 \cdot 1 = 24$.
- Permutaatiot: \begin{align*} &abcd, bcda, cdab, dabc \\ &abdc, bdca, dcab, cabd \\ &acbd, cbda, bdac, dacb \\ &acdb, cdba, dbac, acdb \\ &adbc, dbca, bcad, cadb \\ &adcb, dcba, cbad, badc \\ \end{align*}
- Jos joukossa on 6 alkiota, sillä on $6! = 720$ permutaatiota. Niiden kirjoittaminen paperille kestää 1440 sekuntia eli 24 minuuttia. Tämä on mahdollista tehdä.
Jos joukossa on 7 alkiota, sillä on $7! = 5040$ permutaatiota. Niiden kirjoittaminen paperille kestää 10 080 sekuntia eli 168 minuuttia eli 2 tuntia 48 minuuttia. Tämä alkaa olla rajatapaus.
Jos joukossa on 8 alkiota, sillä on $8! = 40320$ permutaatiota. Niiden kirjoittaminen paperille kestää 22,4 tuntia eli 22 tuntia 24 minuuttia. Tässä ei ole enää järkeä.
Jos joukossa on 9 alkiota, sillä on $9! = 362\,880$ permutaatiota. Niiden kirjoittaminen paperille kestää 8,4 vuorokautta eli 8 vuorokautta 9 tuntia 36 minuuttia. Melko mahdotonta.
Jonoja voidaan muodostaa paitsi järjestämällä jonkin joukon kaikki alkiot jonoon, myös poimimalla jonon alkiot jostain laajemmasta joukosta. Joissain tilanteissa sama alkio voi esiintyä jonossa useammakin kerran. Näitä ilmiöitä tutkitaan seuraavassa tehtävässä.
Järjestysten ja jonojen lukumäärä
Kuinka monta erilaista neljän merkin mittaista jonoa voidaan muodostaa kirjaimista
- A, B, C ja D, jos jokainen kirjain saa esiintyä jonossa enintään kerran
- A, B, C ja D, jos sama kirjain saa esiintyä jonossa useasti
- A, B, C, D, E ja F, jos jokainen kirjain saa esiintyä jonossa enintään kerran
- A, B, C, D, E ja F, jos sama kirjain saa esiintyä jonossa useasti?
VASTAUS
Erilaisia neljän merkin mittaisia jonoja voidaan muodostaa
- $4 \cdot 3 \cdot 2 \cdot 1 = 4! = 24$ kappaletta.
- $4 \cdot 4 \cdot 4 \cdot 4 = 4^4 = 256$ kappaletta.
- $6 \cdot 5 \cdot 4 \cdot 3 = 360$ kappaletta.
- $6 \cdot 6 \cdot 6 \cdot 6 = 6^4 = 1296$ kappaletta.
Seuraavissa tehtävissä tutkitaan jonon muodostamista tilanteessa, jossa jokainen alkio voi tulla valituksi jonoon vain enintään yhden kerran. Tämä ilmaistaan usein sanomalla, että jonon jäsenet poimitaan ilman takaisinpanoa.
Jonojen lukumäärä
Muodostetaan 10 alkion joukosta kuuden alkion jono, jossa mikään alkio ei esiinny useammin kuin yhden kerran.
- Päättele tuloperiaatteen avulla, kuinka monella erilaisella tavalla jono on mahdollista muodostaa.
- Ilmaise a-kohdan tulos muodossa $$ \frac{10!}{x!} $$ valitsemalla kirjaimen $x$ paikalle sopiva luku.
- Miten luvun $x$ voi ilmaista alkioiden määrän (tässä 10) ja jonon pituuden (tässä 6) avulla?
VASTAUS
- Tuloperiaatteen nojalla erilaisia jonoja voidaan muodostaa $$10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 = 151\,200$$ kappaletta.
- Huomataan, että sopiva valinta on $x = 4$: \begin{align*} \frac{10!}{4!} &= \frac{10 \cdots 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{4 \cdot 3 \cdot 2 \cdot 1} \\[2mm] &= 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \end{align*}
- Kysymyksessä on alkioiden määrän ja jonon pituuden erotus: $4 = 10-6$. Kymmenen alkion joukosta voidaan muodostaa kuuden alkion jono $$ \frac{10!}{(10-6)!} $$ eri tavalla.
Jonojen lukumäärä
Muodostetaan $n$ alkion joukosta $k$ alkion jono, jossa mikään alkio ei esiinny useammin kuin yhden kerran.
- Täydennä seuraava taulukko:
Jonon jäsen Vaihtoehtojen määrä 1. jäsen 2. jäsen 3. jäsen $\vdots$ $\vdots$ $k$. jäsen - Päättele tuloperiaatteen avulla, kuinka monella erilaisella tavalla jono on mahdollista muodostaa.
- Ilmaise b-kohdan tulos kahden kertoman osamääränä samaan tapaan kuin edellisessä tehtävässä.
VASTAUS
- Täydennä seuraava taulukko:
Jonon jäsen Vaihtoehtojen määrä 1. jäsen $n$ 2. jäsen $n-1$ 3. jäsen $n-2$ $\vdots$ $\vdots$ $k$. jäsen $n - k + 1$ - Tuloperiaatteen nojalla erilaisia jonoja voidaan muodostaa $$n \cdot (n-1) \cdot (n-2) \cdots (n - k + 1)$$ kappaletta.
- Huomataan, että \begin{align*} &\phantom{ = {} }\frac{n!}{(n-k)!} \\[2mm] &= \frac{n \cdots (n-k+1) \cdot (n-k) \cdots 1}{(n-k) \cdots 2 \cdot 1} \\[2mm] &= n \cdot (n-1) \cdots (n - k + 1) \end{align*}
Tehtävän 1.10 tulos on osa seuraavaa teoreemaa:
TEOREEMA
Joukosta, jossa on $n$ alkiota, muodostetaan $k$ alkion jono.
- Jos jokainen alkio voi esiintyä jonossa enintään yhden kerran, jono voidaan muodostaa $$ \dfrac{n!}{(n-k)!} $$ eri tavalla.
- Jos jokainen alkio voi esiintyä jonossa miten monta kertaa tahansa, jonon voidaan muodostaa $n^k$ eri tavalla.
Ensimmäinen kohta on perusteltu tehtävässä 1.10. Toinen kohta seuraa tuloperiaatteesta.
Summaperiaate – vaihtoehtoiset valinnat
Osajoukkojen lukumäärä
TEHTÄVÄSARJA II
TEHTÄVÄSARJA III
Hajamielinen professori muistaa ystäviensä ovikoodista vain, että se koostuu neljästä erisuuresta parittomasta numerosta.
- Kuinka monta koodia hän joutuu huonoimmassa tapauksessa (enintään) kokeilemaan, jos hän käy systemaattisesti läpi kaikki vaihtoehdot?
- Parin vuoden käyntien jälkeen professori huomaa koodissa seuraavan ominaisuuden: siinä ei ole numeroa 9 eikä peräkkäin "vierekkäisiä" parittomien numeroiden (1 ja 3, 3 ja 1, 3 ja 5, 5 ja 3, 5 ja 7, 7 ja 5, 7 ja 9 tai 9 ja 7) yhdistelmiä. Kuinka monta koodia pitää huonoimmassa tapauksessa kokeilla, kun otetaan huomioon myös nämä lisätiedot?
[Lyhyt K2016/7]
Vastaus
- $5 \cdot 4 \cdot 3 \cdot 2 = 120$ koodia.
- Koodi on joko 3715 tai 5173. Mitkään muut yhdistelmät eivät toteuta kaikkia ehtoja.
Veetun lounaspaikassa on kolmenlaisia pitsoja: 7,50 euron peruspitsa, 8,50 euron ruispitsa ja 10,50 euron pannupitsa. Pitsoihin valitaan 15 täytteestä kaksi erilaista. Maksamalla euron lisää voi valita vielä kolmannen täytteen. Veetu yrittää syödä aina erilaisen pitsan, joka eroaa kaikista aikaisemmista joko pohjaltaan tai täytteiltään.
- Kuinka monta viikkoa hän voi tehdä näin, jos hän syö ravintolassa viisi kertaa viikossa?
- Mikä on erilaisten pitsojen keskimääräinen hinta?
[Lyhyt S2012/8]
Vastaus
- Veetu voi toimia näin 336 viikon ajan.
Erilaisia täytteitä $$ \binom{15}{2} + \binom{15}{3} = 560, $$ joten erilaisia pitsoja $3 \cdot 560 = 1680$. - Peruspitsoja
- kahdella täytteellä 105 kpl, hinta 7,50 euroa
- kolmella täytteellä 455 kpl, hinta 8,50 euroa
- kahdella täytteellä 105 kpl, hinta 8,50 euroa
- kolmella täytteellä 455 kpl, hinta 9,50 euroa
- kahdella täytteellä 105 kpl, hinta 10,50 euroa
- kolmella täytteellä 455 kpl, hinta 11,50 euroa.
Värisävy esimerkiksi www-sivulla ilmoitetaan kuusimerkkisellä RGB-koodilla, joka sisältää tiedon sävyn muodostavien perusvärien punainen (Red), vihreä (Green) ja sininen (Blue) määristä. Kunkin perusvärin määrä ilmoitetaan kahdella peräkkäin kirjoitetulla merkillä, jotka valitaan joukosta
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f.
Laske, kuinka monta erilaista värisävyä RGB-koodilla voidaan ilmaista.
[Lyhyt S2011/9]
Vastaus
Erilaisia sävyjä on $16^6 = 16\,777\,216$ kappaletta.
Kokouksen alussa osanottajat kättelivät toisensa kertaalleen. Kädenpuristuksia tuli tällöin kaikkiaan 66. Kuinka monta osanottajaa kokouksessa oli?
[Lyhyt S2005/6]
Vastaus
Kädenpuristuksia tulee yhtä monta kuin kätteleviä pareja. Jos osanottajia on $n$ kpl, on erilaisia pareja $$ \binom{n}{2} = \frac{n!}{(n-2)!2!} = \frac{n(n-1)}{2}. $$ Saadaan yhtälö $$ \frac{n(n-1)}{2} = 66 $$ eli $$ n^2 - n - 132 = 0. $$ Ratkaisuksi saadaan $n = 12$.
Lottoarvonnassa arvotaan 39 numerosta 7 numeroa. Kuinka monta erilaista 7 rastin lottoruudukkoa on olemassa? Kun on arvottu seitsemän numeroa (eikä ns. lisänumeroita oteta huomioon), erilaisia 4 oikein -ruudukkoja on erään lehtiartikkelin mukaan olemassa 173 600. Tarkista, onko luku oikea. Jos ei, niin mikä on oikea lukumäärä? Laske, kuinka monta erilaista 5 oikein -ruudukkoa ja kuinka monta erilaista 6 oikein -ruudukkoa on olemassa.
[Lyhyt S2003/9]
Vastaus
Erilaisia 7 rastin lottoruudukoita on $$ \binom{39}{7} = \frac{39!}{7!32!} = 15\,380\,937. $$ Erilaisia 4 oikein -ruudukkoja on $$ \binom{7}{4} \cdot \binom{32}{3} = 173\,600. $$ Erilaisia 5 oikein -ruudukkoja on $$ \binom{7}{5} \cdot \binom{32}{2} = 10\,416 $$ ja erilaisia 6 oikein -ruudukkoja on $$ \binom{7}{6} \cdot \binom{32}{1} = 7 \cdot 32 = 224. $$
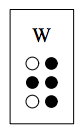
Ranskalaisen Louis Braillen vuonna 1825 kehittämä pistekirjoitus on kohokirjoitusta, jota luetaan sormin. Pistekirjoitusjärjestelmässä kutakin merkkiä kohti on käytettävissä kuusi kiinteää paikkaa, joihin voidaan asettaa yhdestä kuuteen pistettä. (Esimerkkinä kuviossa on kirjain W.) Kuinka monta erilaista merkkiä järjestelmässä voidaan esittää?
[Lyhyt K2007/10]
Vastaus
Jokaisessa paikassa voi olla merkki tai tyhjä kohta, joten erilaisia merkkejä voidaan esittää periaatteessa $2^6 = 64$. Vaihtoehto, jossa kaikki paikat ovat tyhjiä, ei kuitenkaan varsinaisesti ole mikään merkki, joten erilaisia merkkejä on $2^6 - 1 = 64 - 1 = 63$.
- Kuinka monta erilaista istumajärjestystä voidaan muodostaa luokassa, jossa on 30 oppilasta ja 30 pulpettia?
- Kuinka monella tavalla kolme tyhjää pulpettia voidaan valita luokassa, jossa on 27 oppilasta ja 30 pulpettia? Kuinka monta erilaista istumajärjestystä on tässä luokassa?
- Kuinka monta vuotta tietokoneelta kuluisi, jos se kävisi läpi a-kohdan erilaiset istumajärjestykset käsitellen biljoona ($10^{12}$) istumajärjestystä sekunnissa? Yksi vuosi on keskimäärin 365,25 vuorokautta.
[Lyhyt S2006/11]
Vastaus
- $30!$
- Tyhjät pulpetit voidaan valita \begin{align*} \binom{30}{3} &= \frac{30!}{3!27!} \\[2mm] &= \frac{30 \cdot 29 \cdot 28}{3 \cdot 2} \\[2mm] &= 5 \cdot 29 \cdot 28 = 4060 \end{align*} eri tavalla. Erilaisia istumajärjestyksiä on $$ 30 \cdot 29 \cdots 5 \cdot 4 = \frac{30!}{3!} = \frac{30!}{6}. $$
- Noin $8{,}405 \cdot 10^12$ vuotta eli noin 8,4 biljoonaa vuotta.
Ylioppilastutkinnon matematiikan koe muodostuu 10 tehtävästä. Vanhanmuotoisessa matematiikan kokeessa oli 10 tehtävää ja osassa tehtävistä oli kaksi vaihtoehtoa, joista sai laskea vain toisen; uudemmassa kokeessa saa 15 tehtävästä vapaasti valita suoritettavakseen 10 tehtävää. Kuinka monta erilaista 10 tehtävän kokonaisuutta on
- vanhanmuotoisessa kokeessa, jossa viidessä tehtävässä on kaksi vaihtoehtoa
- uudenmuotoisessa kokeessa?
[Lyhyt S2000/8]
Vastaus
- Erilaisia tehtäväkokonaisuuksia on $2^5 = 32$.
- Erilaisia tehtäväkokonaisuuksia on \begin{align*} \binom{15}{10} &= \frac{15!}{10!5!} \\[2mm] &= \frac{15 \cdot 14 \cdot 13 \cdot 12 \cdot 11}{5 \cdot 4 \cdot 3 \cdot 2} \\[2mm] &= 7 \cdot 13 \cdot 3 \cdot 11 \\[1mm] &= 3003. \end{align*}
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

