Eksponenttifunktiot
Luvun tavoitteet
Tämän luvun tavoitteena on, että pystyt eksponenttifunktioiden ja niiden derivaattojen avulla tutkimaan eksponentiaalista kasvua ja vähenemistä. Lisäksi tunnet Neperin luvun erityisominaisuudet eksponenttifunktion kantalukuna ja tiedät, mitä luonnollinen logaritmi tarkoittaa. Osaat
- hahmotella eksponenttifunktion kuvaajan eri kantalukujen tapauksessa
- ratkaista yksinkertaisia eksponenttiyhtälöitä logaritmin avulla
- määrittää eksponenttifunktion derivaattafunktion
- soveltaa aiemmin oppimiasi derivointisääntöjä eksponenttifunktioista muodostettujen funktioiden kulun tutkimiseen
- tutkia eksponenttifunktioiden avulla ilmiöitä, joihin liittyy eksponentiaalista kasvua tai vähenemistä.
Eksponenttifunktiot
Kurssissa MAA2 tutustuttiin niin sanottuihin potenssifunktioihin, jotka ovat muotoa $$f(x) = x^n,$$ missä $n$ on positiivinen kokonaisluku. Tuttuja esimerkkejä potenssifunktioista ovat toisen asteen potenssifunktio $f(x) = x^2$ ja kolmannen asteen potenssifunktio $g(x) = x^3$.
Jos muuttuja vaihdetaan kantaluvun paikalta eksponentiksi, saadaan joukko funktioita, joita kutsutaan eksponenttifunktioiksi.
MÄÄRITELMÄ: EKSPONENTTIFUNKTIO
Oletetaan, että $k \neq 1$ on positiivinen reaaliluku. Funktioita, jotka ovat muotoa $$f(x) = k^x,$$ sanotaan eksponenttifunktioiksi.
Eksponenttifunktiot
Tutki tämän Geogebra-havainnollistuksen avulla, miltä erilaisten eksponenttifunktioiden kuvaajat näyttävät, ja vastaa seuraaviin kysymyksiin:
- Mikä ehto kantaluvun $k > 0$ pitää toteuttaa, jotta eksponenttifunktion $f(x) = k^x$ kuvaaja näyttää samantyyppiseltä kuin alla?
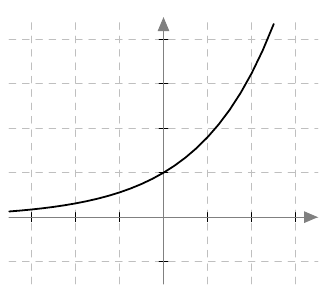
- Mikä ehto kantaluvun $k > 0$ pitää toteuttaa, jotta eksponenttifunktion $f(x) = k^x$ kuvaaja näyttää samantyyppiseltä kuin alla?
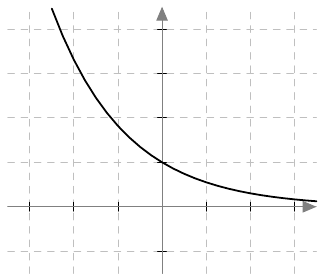
- Miksi funktiota $f(x) = 1^x$ ei yleensä kutsuta eksponenttifunktioksi? Mikä on sille osuvampi nimi?
- Millaisia arvoja eksponenttifunktiot saavat?
VASTAUS
- $k > 1$
- $0 < k < 1$
- Funktio $f(x) = 1^x$ on vakiofunktio $x \mapsto 1$.
- Eksponenttifunktiot saavat vain positiivisia arvoja.
Eksponenttifunktioiden avulla voidaan kuvata eksponentiaalista kasvua ja vähenemistä. Nämä ovat ilmiöitä, joissa jokin asia kasvaa tai vähenee niin, että se säännöllisin väliajoin tulee $k$-kertaiseksi aina edelliseen tilanteeseen verrattuna. Seuraavissa tehtävissä tutustutaan joihinkin esimerkkeihin.
Eksponenttifunktiot
Intian väliluku oli noin 616 miljoonaa vuonna 1979 ja vuotta myöhemmin noin 630 miljoonaa. Tuolloin laadittiin väestöennuste vuodelle 2000 olettaen, että vuotuinen väestönkasvuprosentti pysyy samana.
- Mikä oli Intian vuotuinen väestönkasvuprosentti 1970-luvun lopussa? Anna vastaus kolmen merkitsevän numeron tarkkuudella.
- Muodosta funktio $f(t)$, joka antaa ennusteen Intian väkiluvulle, kun vuodesta 1979 on kulunut $t$ vuotta. Miten tämä funktio liittyy eksponenttifunktioihin?
- Mikä Intian väkiluku oli ennusteen mukaan vuonna 2000?
- Intian väkiluku oli vuonna 2013 noin 1 221 miljoonaa. Kuinka monta prosenttia suurempi tai pienempi oli vuodelle 2013 ennustettu väkiluku?
VASTAUS
- Vuotuinen väestönkasvu oli noin 2,27 %.
- Ennuste saadaan funktiosta $$ f(t) = 616 \cdot 10^6 \cdot \left(\frac{630}{616}\right)^t. $$ Tässä vuosittaiselle kasvukertoimelle on käytetty tarkkaa arvoa, jotta ennusteeseen tulee mahdollisimman vähän pyöristysvirhettä. Huomaa kuitenkin, että vuosittainen kasvukerroin on $$ \frac{630}{616} \approx 1{,}0227. $$ Funktio $f$ on eksponenttifunktio vakiolla $616 \cdot 10^6$ kerrottuna. Kantalukuna on kasvukerroin $$ \frac{630}{616}. $$
- Ennusteen mukaan Intian väkiluku vuonna 2000 oli $f(21) \approx 988$ miljoonaa.
- Ennusteen mukaan Intian väkiluku vuonna 2013 oli $f(34) \approx 1\,323$ miljoonaa. Tämä oli noin 8,35 % suurempi kuin todellinen väkiluku.
Eksponenttifunktiot
Tshernobylin ydinvoimalaonnettomuudessa 26.4.1986 vapautui ilmaan mm. radioaktiivista cesiumia, jonka puoliintumisaika on noin 30 vuotta. Tämä tarkoittaa, että 30 vuoden aikana aina puolet jäljellä olevista cesium-atomeista hajoaa toisen alkuaineen atomeiksi.
Jäljellä olevan radioaktiivisen cesiumin suhteellista osuutta voidaan kuvata funktiolla $$ f(t) = k^{\frac{t}{T}}, $$ missä muuttuja $t$ ilmaisee alkuhetkestä kuluneen ajan vuosina.
- Tiedetään, että 30 vuoden kuluttua radioaktiivisesta cesiumista on jäljellä puolet eli $$ f(30) = 0{,}5. $$ Valitse tämän tiedon avulla sopivat luvut funktion $f$ lausekkeeseen kantaluvuksi $k$ ja vakioksi $T$.
Vinkki: voit kokeilla erilaisia ideoita ja katsoa, mikä antaa oikean tuloksen. - Kuinka suuri osuus radioaktiivisesta cesiumista on jäljellä 60 vuoden kuluttua? Tarkista, että saat saman tuloksen sekä päättelemällä että a-kohdan funktion avulla.
- Kuinka monta prosenttia radioaktiivisesta cesiumista on jäljellä 26.4.2025? Anna vastaus kahden merkitsevän numeron tarkkuudella.
VASTAUS
- Kantaluku on $k = 0{,}5$ ja vakio $T = 30$. Siis $$ f(t) = 0{,}5^{\frac{t}{30}}, $$ missä $t$ on kulunut aika vuosina.
- Kun 60 vuotta on kulunut, cesiumin määrä on ehtinyt puoliintua kaksi kertaa, joten jäljellä on neljäsosa. $$ f(60) = 0{,}5^{\frac{60}{30}} = 0{,}5^2 = 0{,}25. $$
- Vuosia ehtii kulua $$ 2025-1986 = 39, $$ joten jäljellä olevan cesiumin osuus on $$ f(39) = 0{,}5^{\frac{39}{30}} \approx 0{,}41 $$ eli noin 41 %.
Eksponenttifunktiot
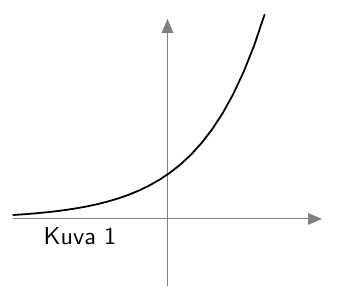
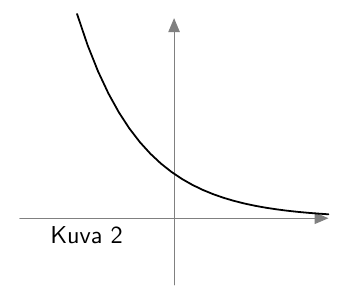
Alla on lueteltu erilaisia tilanteita, joissa voidaan hyödyntää matemaattisia malleja. Päättele, sopiiko malliksi eksponentiaalisen kasvun malli (kuva 1), eksponentiaalisen vähenemisen malli (kuva 2) vai ei kumpikaan.
- Bakteerien määrän ennustaminen, kun tiedetään, että bakteeriviljelmän koko kolminkertaistuu aina kahden tunnin välein.
- Lääkeaineen annostelun suunnittelu, kun tiedetään, että kyseisen lääkeaineen pitoisuus elimistössä puolittuu viidessä tunnissa.
- Saaren kanipopulaation koon ennustaminen, kun tiedetään, että suotuisissa oloissa kanien lukumäärä kaksinkertaistuu vuosittain.
- Hintojen kehityksen ennustaminen pitkällä aikavälillä, kun vuosittaiseksi kuluttajahintojen nousuksi eli inflaatioksi arvioidaan 1,5 %.
VASTAUS
- Kuva 1: eksponentiaalinen kasvu.
- Kuva 2: eksponentiaalinen väheneminen.
- Kuva 1: eksponentiaalinen kasvu.
- Kuva 1: eksponentiaalinen kasvu.
Tehtävän 2.1 havainnot voidaan koota seuraavaksi teoreemaksi, jonka täsmälliseen perusteluun ei nyt ole tarkoituksenmukaista syventyä.
TEOREEMA
Oletetaan, että $k \neq 1$ on positiivinen reaaliluku. Eksponenttifunktion $$ f(x) = k^x $$ määrittelyjoukko on koko lukusuora $\R$ ja arvojoukko on väli $\pa 0, \infty \pe$.
Jos kantaluku $k > 1$, eksponenttifunktio on aidosti kasvava:
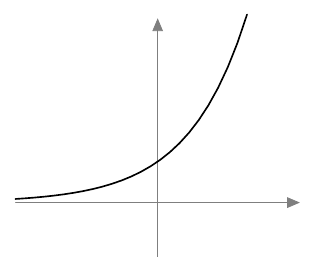
Jos kantaluku $0 < k < 1$, eksponenttifunktio on aidosti vähenevä: 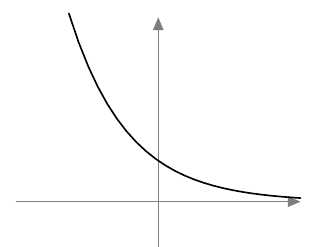
Eksponenttifunktiot
Millä vakion $c$ arvoilla eksponenttifunktio $$ f(x) = (2c - 3)^x $$ on
- aidosti kasvava
- aidosti vähenevä?
VASTAUS
- $c > 2$
- $\frac{3}{2} < c < 2$
Kun tutkitaan, missä kohdassa eksponenttifunktio saa tietyn arvon, päädytään ratkaisemaan niin sanottu eksponenttiyhtälö. Esimerkiksi alla olevasta eksponenttifunktion $f(x) = 2^x$ kuvaajasta nähdään, että yhtälöllä $$ 2^x = 3 $$ on täsmälleen yksi ratkaisu:
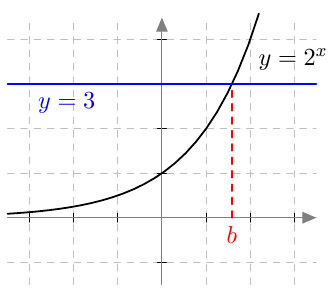
Kurssilla MAY1 opittiin, että kuvaan kirjaimella $b$ merkittyä ratkaisua sanotaan luvun 3 kaksikantaiseksi logaritmiksi. Siis $2^x = 3$, jos ja vain jos $x = \log_2(3)$.
Teoreemaan 1 kootuista eksponenttifunktion ominaisuuksista seuraa, että eksponenttiyhtälöllä $$ k^x = a $$ on täsmälleen yksi ratkaisu, olipa $a$ mikä tahansa positiivinen reaaliluku. Tämä tarkoittaa, että seuraava MAY1-kurssilta tuttu määritelmä määrittelee kaikkien positiivisten lukujen logaritmit yksikäsitteisesti ja aukottomasti.
MÄÄRITELMÄ: LOGARITMI
Oletetaan, että kantaluku $k$ on positiivinen ja $k \neq 1$. Positiivisen luvun $a$ $k$-kantainen logaritmi tarkoittaa yhtälön $$k^x = a$$ ratkaisua. Sitä merkintään $\log_k(a)$.
Logaritmin määritelmästä siis seuraa, että $$ k^{\log_k(a)} = a. $$
Logaritmin merkintää käyttäen edellinen kuva näyttää tältä:
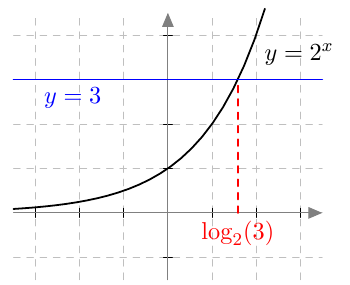
Eksponentin ratkaiseminen
Ratkaise eksponenttiyhtälö
- $2^x = 500$
- $\left(\dfrac{7}{5}\right)^x = 6$.
Anna vastauksen tarkka arvo logaritmin avulla ilmaistuna sekä likiarvo kolmen merkitsevän numeron tarkkuudella. Likiarvoja erikantaisille logaritmeille saat laskettua esimerkiksi Geogebran laskimella.
VASTAUS
- $x = \log_2(500) \approx 8{,}97$
- $x = \log_\frac{7}{5}(6) \approx 5{,}33$
Kantalukuna Neperin luku
Edellisessä luvussa tarkasteltiin erilaisia eksponenttifunktioita. Niistä matematiikan kannalta tärkein ja laajasti sovelluksissa käytetty on funktio $$ f(x) = e^x, $$ jonka kantalukuna on niin sanottu Neperin luku $e$. Tämä luku on löydetty 1600-luvulla ja se on saanut nimensä skotlantilaisen matemaatikon John Napierin mukaan. Neperin luku $e$ on irrationaaliluku, jonka likiarvo kymmenen desimaalin tarkkuudella on $2{,}7182818285$. Sen likiarvoja saadaan laskettua lukujonon $$ \left(1 + \frac{1}{1}\right)^1, \left(1 + \frac{1}{2}\right)^2, \left(1 + \frac{1}{3}\right)^3, \ldots $$ avulla. Voit kokeilla, millaisen likiarvon saat esimerkiksi tämän jonon miljoonannesta jäsenestä laskemalla lausekkeen $$ \left(1 + \frac{1}{n}\right)^n $$ arvon, kun $n = 10^6$.
Neperin luvun merkitys johtuu pitkälti siitä, että eksponenttifunktiolla $$ f(x) = e^x $$ on erityinen kasvunopeus. Sitä tutkitaan seuraavassa tehtävässä.
Eksponenttifunktion kasvunopeus
Tutki $e$-kantaisen eksponenttifunktion derivaattaa tämän Geogebra-havainnollistuksen avulla. Päättele vastaukset seuraaviin kysymyksiin:
- Miten oranssin pisteen $y$-koordinaatti ja tangentin kulmakerroin liittyvät toisiinsa?
- Miten oranssin pisteen $y$-koordinaatti ja eksponenttifunktion arvo liityvät toisiinsa?
- Selitä omin sanoin, mitä erikoista $e$-kantaisen eksponenttifunktion kasvunopeudessa on.
- Mikä on funktion $f(x) = e^x$ derivaattafunktio?
VASTAUS
- Oranssin pisteen $y$-koordinaatti on samaan kohtaan piirretyn tangentin kulmakerroin. Oranssi piste on siis derivaattafunktion kuvaajan piste.
- Oranssin pisteen $y$-koordinaatti on sama kuin eksponenttifunktion arvo, sillä oranssi piste on myös eksponenttifunktion kuvaajan piste.
- Eksponenttifunktion $f(x) = e^x$ kasvunopeus on jokaisessa kohdassa sama kuin funktion arvo.
- Funktion $f(x) = e^x$ derivaattafunktio on funktio $f(x) = e^x$ itse.
Neperin luku on eksponenttifunktion kantalukuna niin yleisesti käytetty, että monesti eksponenttifunktiosta puhuttaessa tarkoitetaan nimenomaan $e$-kantaista eksponenttifunktiota $f(x) = e^x$.
Seuraavassa tehtävässä tutustutaan yhteen monista eksponenttifunktion sovelluksista.
Eksponentiaalinen kasvu ja väheneminen
Tavallisissa lämpötiloissa kappaleen jäähtyminen noudattaa kohtuullisella tarkkuudella niin sanottua Newtonin jäähtymislakia, jonka mukaan kappaleen ja ympäristön lämpötilaeroa voidaan kuvata funktiolla $$ d(t) = d_0e^{-kt}. $$ Tässä $d(t)$ on lämpötilaero $t$ tunnin kuluttua, $d_0$ on lämpötilaero alkuhetkellä $t = 0$ ja $k$ on tilannekohtainen vakio, joka riippuu esimerkiksi kappaleen muodosta ja materiaalista.
Sähkökatkoksen alkaessa sähkölämmitteisen rakennuksen sisälämpötila on $20\ {}^\circ\text{C}$ ja ulkona on $15\ {}^\circ\text{C}$ pakkanen. Vakion $k$ arvo on selvitetty rakennukselle jo aikaisemmin ja se on $k = 0{,}05$.
- Mikä on rakennuksen sisälämpötila kahden tunnin kuluttua sähkökatkoksen alkamisesta?
- Kuinka monta prosenttia rakennuksen sisälämpötila laskee sähkökatkoksen viiden ensimmäisen tunnin aikana?
- Piirrä lämpötilaeroa kuvaavan funktion kuvaaja esimerkiksi Geogebralla. Tutki sen avulla graafisesti, milloin rakennuksen sisälämpötila putoaa pakkasen puolelle.
VASTAUS
- Noin $16{,}7\ {}^\circ\text{C}$.
- Noin 39 %.
Viiden tunnin kuluttua sisälämpötila on noin $12{,}3\ {}^\circ\text{C}$. - Sisälämpötila putoaa pakkasen puolelle, kun sähkökatkon alkamisesta on kulunut noin 17 tuntia.
(Lämpötilaeroa kuvaavan funktion kuvaaja painuu suoran $y = 15$ alle kohdassa $x \approx 16{,}95$.)
Eksponenttiyhtälö voidaan ratkaista logaritmin avulla myös silloin, kun kantalukuna on Neperin luku $e$. Vastaavaa logaritmia kutsutaan luonnolliseksi logaritmiksi.
MÄÄRITELMÄ: LUONNOLLINEN LOGARITMI
Positiivisen luvun $a$ luonnollinen logaritmi tarkoittaa yhtälön $$e^x = a$$ ratkaisua $\log_e(a)$. Sille käytetään merkintää $\ln(a)$.
Luonnollisen logaritmin määritelmästä siis seuraa, että $$ e^{\ln(a)} = a. $$
Esimerkiksi yhtälön $$ e^x = 4 $$ ratkaisua voidaan havainnollistaa koordinaatistossa:
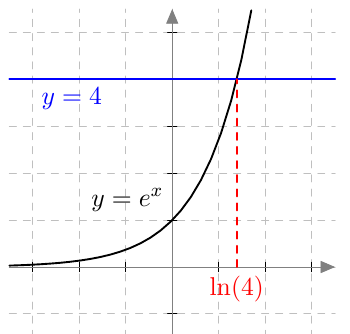
Eksponentin ratkaiseminen
Ratkaise seuraavat yhtälöt. Anna vastauksena tarkka arvo ja likiarvo kolmen merkitsevän numeron tarkkuudella.
- $e^x = 2$
- $5e^{x} - 15 = 0$
- $8e^{3x - 1} - 7 = 1$
VASTAUS
- $x = \ln(2) \approx 0{,}693$.
- $x = \ln(3) \approx 1{,}10$.
- $x = \dfrac{1}{3} \approx 0{,}333$.
Huom. välivaiheena saadaan yhtälö $$3x - 1 = \ln(1)$$ eli yhtälö $$3x - 1 = 0.$$
Luonnollisen logaritmin määritelmä
Sievennä seuraavat lausekkeet luonnollisen logaritmin määritelmän avulla:
- $e^{\ln(5)}$
- $\ln (e^8)$
- $e^{\ln(1)}$
- $\ln (e^{-1})$
VASTAUS
- Luonnollisen logaritmin määritelmän mukaan $\ln(5)$ on yhtälön $e^x = 5$ ratkaisu. Siten $$e^{\ln(5)} = 5.$$
- Luonnollisen logaritmin määritelmän mukaan $\ln (e^8)$ on yhtälön $e^x = e^8$ ratkaisu. Koska funktion $f(x) = e^x$ on aidosti kasvava ja saa jokaisen arvonsa vain kerran, niin yhtälö toteutuu, jos ja vain jos eksponentit ovat samat eli $x = 8$. Siis $$\ln (e^8) = 8.$$
- Luonnollisen logaritmin määritelmän mukaan $\ln(1)$ on yhtälön $e^x = 1$ ratkaisu. Siten $$e^{\ln(1)} = 1.$$
- Luonnollisen logaritmin määritelmän mukaan $\ln (e^{-1})$ on yhtälön $e^x = e^{-1}$ ratkaisu. Koska funktion $f(x) = e^x$ on aidosti kasvava ja saa jokaisen arvonsa vain kerran, niin yhtälö toteutuu, jos ja vain jos eksponentit ovat samat eli $x = -1$. Siis $$\ln (e^{-1}) = -1.$$
Eksponenttifunktion derivaatta
Tehtävässä 2.7 havaittiin, että eksponenttifunktion $f(x) = e^x$ tangentin kulmakerroin eli derivaatan arvo on jokaisessa kohdassa sama kuin funktion arvo:
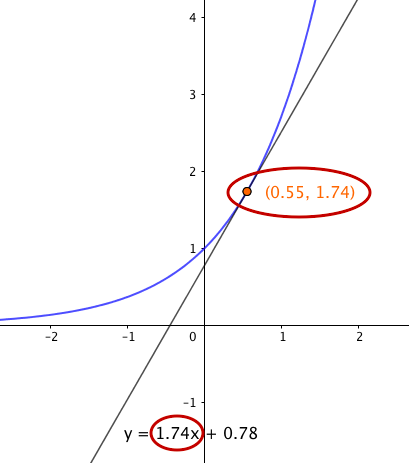
Derivaattafunktion kuvaaja on siten sama kuin alkuperäisen eksponenttifunktion kuvaaja:
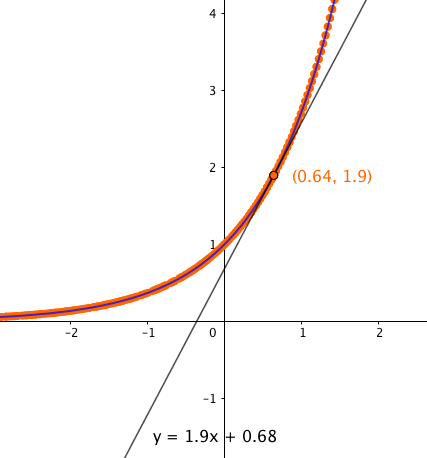
Tästä havainnosta saadaan seuraava teoreema, jonka täsmälliseen todistukseen tutustutaan matematiikan yliopisto-opinnoissa.
TEOREEMA
Eksponenttifunktio $f(x) = e^x$ on kaikkialla derivoituva ja sen derivaattafunktio on $$ f'(x) = e^x. $$
Teoreeman 7 tulos voidaan ilmaista myös merkinnällä $$ \mathop{\mathrm{D}} e^x = e^x. $$
Eksponenttifunktion derivaatta
Eksponenttifunktion $f(x) = e^x$ kuvaajalle piirretään origon kautta kulkeva tangentti. Tehtävänä on selvittää, missä pisteessä tangentti sivuaa kuvaajaa.
- Piirrä tilanteesta mallikuva.
- Mitä voit päätellä tangentin yhtälöstä sen perusteella, että tangentti kulkee origon kautta?
- Merkitään sivuamispisteen $x$-koordinaattia kirjaimella $a$. Mikä on sivuamispisteen $y$-koordinaatti? Entä mikä on tangentin kulmakerroin?
- Sivuamispisteen koordinaatit toteuttavat tangenttisuoran yhtälön. Muodosta tämän tiedon avulla sopiva yhtälö ja selvitä, missä pisteessä tangentti sivuaa kuvaajaa.
VASTAUS
-
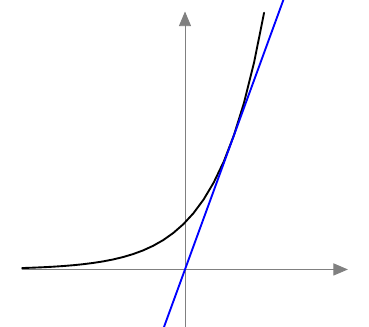
- Tangentin yhtälö on muotoa $y = kx$ eli vakiotermi $h = 0$.
- Sivuamispisteen $y$-koordinaatti on funktion arvo $f(a) = e^a$. Tangentin kulmakerroin on derivaatan arvo $f'(a) = e^a$.
- Kun yhtälöön $$y = kx$$ sijoitetaan $y = e^a$, $k = e^a$ ja $x = a$, saadaan yhtälö $$ e^a = e^a\cdot a, $$ josta saadaan ratkaistua $a = 1$. Sivuamispiste on siis $(1,e)$.
Kun eksponenttifunktion derivaattafunktio nyt tunnetaan, voidaan entistä useampien funktioiden kulkua tutkia derivaatan avulla kuten MAA6-kurssilla opittiin. Tätä harjoitellaan seuraavassa tehtävässä.
Eksponenttifunktion derivaatta
Tehtävänä on osoittaa, että käyrä $$y = e^x - x - 1$$ on suoran $2x - 2y - 1 = 0$ yläpuolella.
- Muokkaa suoran yhtälö muotoon $y = kx + h$.
- Mikä ehto lausekkeiden $e^x - x - 1$ ja $kx + h$ pitää toteuttaa, jotta käyrä on suoran yläpuolella?
- Muodosta sopiva funktio ja määritä sen pienin arvo. Päättele tästä, että b-kohdan ehto toteutuu.
VASTAUS
- $y = x - \frac{1}{2}$.
- Kaikilla muuttujan $x$ arvoilla pitää päteä epäyhtälö $$e^x - x - 1 > x - \frac{1}{2}.$$
- Funktioksi voidaan valita $$ f(x) = e^x - 2x - \frac{1}{2}. $$ Sen derivaattafunktiolla $$ f'(x) = e^x - 2 $$ on yksi nollakohta $x = \ln (2)$. Kulkukaaviosta nähdään, että funktio $f$ saa tässä pienimmän arvonsa $$f(\ln(2)) = \frac{3}{2} - 2\ln(2) \approx 0{,}11 > 0.$$ Siis $f(x) > 0$ kaikilla muuttujan $x$ arvoilla, joten $$e^x - x - 1 > x - \frac{1}{2}$$ kaikilla muuttujan $x$ arvoilla.
Yhdistetyn funktion derivointisäännön avulla pystytään derivoimaan erilaisia ekponenttifunktiosta yhdistettyjä funktioita.
Eksponenttifunktion derivaatta
Derivoi seuraavat funktiot. Kertaa tarvittaessa yhdistetyn funktion derivointisääntö MAA7-kurssin teoreemasta 23.
- $f(x) = e^{-2x}$
- $g(x) = e^{\sin x}$
- $h(x) = e^{1+x^2}$
VASTAUS
- $f'(x) = -2e^{-2x}$.
- $g'(x) = e^{\sin x} \cos x$.
- $h'(x) = 2xe^{1 + x^2}$
Eksponenttifunktion derivaatta
Tutki, onko funktiolla $$ f(x) = xe^{-x} $$ suurinta tai pienintä arvoa. Jos kyseinen arvo on olemassa, mikä se on?
VASTAUS
Funktiolla on suurin arvo $$ f(1) = \frac{1}{e} $$ mutta ei pienintä arvoa.
Derivaattafunktiolla \begin{align*} f'(x) &= e^{-x} -xe^{-x} \\ &= e^{-x} (1 - x) \end{align*} on yksi nollakohta $x = 1$. Kulkukaavion perusteella päätellään, että funktio saa tässä kohdassa suurimman arvonsa.
Eksponenttifunktion derivaatta
Tehtävänä on osoittaa, että funktio $$ f(x) = e^{2x} - 2e^x + x $$ on kaikkialla aidosti kasvava.
- Muodosta derivaattafunktio $f'(x)$.
- Muodosta yhtälö $f'(x) = 0$. Merkitse $e^x = t$, jolloin yhtälön ainoaksi tuntemattomaksi jää $t$ ja yhtälön ratkaisu helpottuu.
Vinkki: potenssin potenssin laskusääntö (MAY1-kurssin teoreema 1). - Onko derivaattafunktiolla nollakohtia? Minkä merkkisiä arvoja derivaattafunktio saa?
- Perustele omin sanoin, miten edellisten kohtien perusteella voidaan päätellä, että funktio $f$ on kaikkialla aidosti kasvava.
VASTAUS
- $f'(x) = 2e^{2x} - 2e^x + 1$
- Kun merkitään $e^x = t$, yhtälö $$2(e^{x})^2 - 2e^x + 1 = 0$$ saadaan muotoon $$2t^2 - 2t + 1 = 0.$$
- Yhtälöllä $$2t^2 - 2t + 1 = 0$$ ei ole ratkaisuja, joten derivaattafunktiolla ei ole nollakohtia. Koska esimerkiksi $$f'(0) = 2e^0 - 2e^0 + 1 = 1 > 0,$$ on derivaattafunktion arvo aina positiivinen.
- Koska derivaattafunktion arvo on kaikkialla positiivinen, on funktio $f$ kaikkialla aidosti kasvava.
Luonnollisen logaritmin määritelmän ja yhdistetyn funktion derivointisäännön avulla saadaan johdettua derivaattafunktiot myös niille eksponenttifunktioille, joiden kantalukuna ei ole Neperin luku.
Eksponenttifunktion derivaatta
Oletetaan, että $k \neq 1$ on positiivinen reaaliluku. Tehtävänä on määrittää eksponenttifunktion $f(x) = k^x$ derivaattafunktio.
- Ilmaise luku $k$ Neperin luvun $e$ ja luonnollisen logaritmin avulla.
Vinkki: Palauta mieleesi luonnollisen logaritmin määritelmä ja siitä seuraavat yhtälöt. - Sijoita a-kohdan lauseke eksponenttifunktion lausekkeeseen kantaluvun $k$ paikalle ja sievennä potenssien laskusääntöjen avulla.
Vinkki: Potenssien laskusääntöjä voit kerrata MAY1-kurssin teoreemasta 1. - Määritä funktion $f$ derivaattafunktio.
Vinkki: b-kohdan lauseke ja yhdistetyn funktion derivointisääntö.
VASTAUS
- Luonnollisen logaritmin määritelmästä seuraa, että $$ e^{\ln(k)} = k. $$
- $$ f(x) = k^x = \left(e^{\ln(k)}\right)^x = e^{x\ln(k)} $$
- \begin{align*} f'(x) &= e^{x\ln (k)} \ln (k)\\ &= k^x \ln(k) \end{align*}
Tehtävän 2.17 tuloksena saadaan seuraava teoreema:
TEOREEMA
Oletetaan, että $k \neq 1$ on positiivinen reaaliluku. Eksponenttifunktio $f(x) = k^x$ on kaikkialla derivoituva ja sen derivaattafunktio on $$ f'(x) = k^x \ln(k). $$
Perustelu tehtävässä 2.17.
Eksponenttifunktion derivaatta
Derivoi seuraavat funktiot. Kertaa tarvittaessa yhdistetyn funktion derivointisääntö MAA7-kurssin teoreemasta 23.
- $f(x) = 2^x$
- $g(x) = 3^{-x}$
- $h(x) = 10^{2x}$
VASTAUS
- $f'(x) = 2^x \ln(2)$.
- $g'(x) = -3^{-x} \ln(3)$.
- $h'(x) = 2 \ln(10) \cdot 10^{2x}$
Eksponenttifunktion derivaatta
Jos raakaa jauhelihaa säilytetään huoneenlämmössä, lihassa olevien bakteerien määrä noin 7,9-kertaistuu joka tunti. Arvioidaan, että bakteerien lukumäärä jauhelihaerässä on nyt noin 1500.
- Muodosta funktio $B(t)$, joka ilmaisee bakteerien määrän $t$ tunnin kuluttua.
- Kuinka paljon bakteereita jauhelihassa on, jos se unohtuu keittiön pöydälle 1,5 tunniksi?
- Millä nopeudella bakteerien määrä lisääntyy hetkellä $t = 1{,}5$? Entä hetkellä $t = 3$?
VASTAUS
- Kantaluku voidaan valita kahdella tavalla: $$B(t) = 1500 \cdot 7{,}9^t$$ tai $$B(t) = 1500 \cdot e^{t \ln (7{,}9)}.$$
- Noin 33 000 kpl.
- Derivaattafunktio on $$B'(t) = 1500 \cdot \ln (7{,}9) \cdot 7{,}9^t,$$ joten $$ B'(1{,}5) \approx 69\,000 $$ ja $$ B'(3) \approx 1\,500\,000. $$ Bakteerien määrä lisääntyy siis 1,5 tunnin kuluttua noin 69 000 bakteeria tunnissa ja 3 tunnin kuluttua noin 1,5 miljoonaa bakteeria tunnissa.
TEHTÄVÄSARJA II
Eksponenttifunktiot
Vanhemmat sijoittivat lastensa nimiin yhtä suuret rahasummat. Esikoisen osuus sijoitettiin pankkitilille, jonka nimellinen vuosikorko oli 5 %. Korkotuloista kuitenkin perittiin vuosittain 30 % lähdevero, minkä vuoksi talletus kasvoi vuosittain korkoa 3,5 %.
Kuopuksen osuus sijoitettiin osakkeisiin, joiden arvon kasvoi keskimäärin noin 4 % vuodessa. Kymmenen vuoden kuluttua nuorempi lapsista myi osakkeensa pois ja maksoi niiden arvonnoususta 30 % pääomatuloveron. Kummalla oli tällöin enemmän rahaa? Kuinka monta prosenttia enemmän?
Vinkki: Voit ensin valita jonkin sopivan rahasumman ja laskea laskun sen avulla. Sen jälkeen voit kuvata rahasummaa jollakin kirjaimella ja tarkistaa samojen laskutoimitusten avulla, ettei tulos riipu rahasumman suuruudesta.
Vastaus
Merkitään alkuperäistä yhden lapsen nimiin sijoitettua rahasummaa kirjaimella $a$. Esikoisen rahasumma 10 vuoden kuluttua oli $$ 1{,}035^{10} \cdot a \approx 1{,}411a. $$ Kuopuksen osakkeiden arvo oli $$ 1{,}04^{10}a \approx 1{,}480a. $$ Arvonnoususta meni 30 % vero, minkä jälkeen rahaa jäi noin $$ 0{,}7 \cdot 0{,}480a + a = 1{,}336a. $$ Esikoisella oli siis enemmän rahaa, tarkemmin sanottuna noin 5,6 % enemmän kuin kuopuksella.
Eksponenttifunktiot
Bakteeriviljelmä kaksinkertaistui kolmessa tunnissa. Kuinka monta bakteeria viljelmässä on 20 tunnin kuluttua, jos niitä 5 tunnin kuluttua oli noin 600 000?
Vastaus
Bakteerien määrää $t$ tunnin kuluttua kuvaa likimain funktio $$ B(t) = 188\,988 \cdot 2^{\frac{t}{3}} $$ joten 20 tunnin kuluttua bakteereja on noin $B(20) \approx 19\,000\,000$.
Eksponenttifunktiot
Olkoon radioaktiivisen aineen puoliintumisaika $T$. Selvitä, kuinka monta prosenttia kyseisen aineen atomeista on jäljellä, kun aikaa on kulunut
- $2T$
- $\dfrac{T}{2}$
- $10T$.
Vastaus
Atomeista on jäljellä
- $\left(\dfrac{1}{2}\right)^\frac{2T}{T} = \dfrac{1}{4}$ eli 25 %.
- $\left(\dfrac{1}{2}\right)^\frac{T}{2T} = \dfrac{1}{\sqrt{2}}$ eli noin 71 %.
- $\left(\dfrac{1}{2}\right)^\frac{10T}{T} = \dfrac{1}{1024}$ eli noin 0,098 %.
Eksponenttifunktiot
Tshernobylin ydinvoimalaonnettomuuden seurauksena Suomeen tullut radioaktiivinen laskeuma sisälsi liukenevaa cesiumia, jonka puoliintumisaika eläimissä on 3 kuukautta. Kuinka monta prosenttia laskeuman radioaktiivisesta cesiumista oli eläimissä jäljellä 1,5 vuoden kuluttua onnettumuudesta lokakuun lopussa 1987?
Vastaus
Olkoon cesiumin määrä alussa $a$. Määrä $t$ kuukauden kuluttua saadaan funktiosta $$ f(t) = a \cdot \left(\frac{1}{2}\right)^\frac{t}{3}. $$ Lokakuun lopussa vuonna 1987 cesiumia oli $$ f(18) = a \cdot \left(\frac{1}{2}\right)^\frac{18}{3} = 0{,}015625a. $$ Jäljellä oli siis noin 1,6 % alkuperäisestä määrästä.
Eksponenttifunktio
Oletetaan, että $k > 0$ ja $k \neq 1$. Ratkaise potenssin laskusääntöjen ja eksponenttifunktion ominaisuuksien avulla yhtälö
- $k^5\cdot k^x = k^{3x}$
- $\dfrac{k^x}{k^4} = k^{\frac{x}{3}}$
Vastaus
- $x = \dfrac{5}{2}$
(Koska eksponenttifunktio on aidosti monotoninen riippumatta kantaluvusta $k$, saadaan yhtälö $5 + x = 3x$.) - $x = 6$
(Koska eksponenttifunktio on aidosti monotoninen riippumatta kantaluvusta $k$, saadaan yhtälö $x-4 = \frac{x}{3}$.)
Eksponenttifunktiot
Oletetaan, että $k > 0$ ja $a \in \R$. Osoita, että funktiolla $f(x) = k^x$ on ominaisuus $$ f(ax) = \left(f(x)\right)^a. $$
Vastaus
Sovelletaan funktion $f$ määritelmää ja potenssien laskusääntöjä: \begin{align*} f(ax) &= k^{ax} = \left(k^x\right)^a = \left(f(x)\right)^a. \end{align*}
Eksponentiaalinen kasvu ja väheneminen
Elävät kasvit sisältävät radioaktiivista hiilen isotooppia ${}^{14}\text{C}$. Tämän vuoksi kasvien radioaktiivisuus massayksikköä kohti on $$ \frac{A_0}{m} \approx 0{,}23 \, \frac{\text{Bq}}{\text{g}}. $$ Tässä $A_0$ on kasvinäytteen aktiivisuus (yksikkönä Becquerel) ja $m$ on kasvinäytteen sisältämän hiilen massa (yksikkönä gramma). Kasvin kuoltua hiilen aktiivisuuden vähenemistä voidaan kuvata funktiolla $$ A(t) = A_0e^{-kt}. $$ Tässä $A(t)$ on kasvinäytteen aktiivisuus $t$ vuoden kuluttua ja $k \approx 1{,}20968\cdot 10^{-4}$.
Tehtävänä on selvittää, kuinka monta prosenttia kasvin radioaktiivisuus massayksikköä kohti vähenee 2000 vuoden aikana kasvin kuoltua (olettaen, että kasvi ei maadu vaan säilyy esimerkiksi ikiroudan suojassa).
- Elävästä kasvista otetaan näyte, joka sisältää 1 gramman hiiltä. Mikä on näytteen aktiivisuus $A_0$?
- Mikä on yhden hiiligramman aktiivisuus 2000 vuoden kuluttua?
- Kuinka monta prosenttia kasvin radioaktiivisuus massayksikköä kohti on vähentynyt 2000 vuoden aikana kasvin kuoltua?
Vastaus
- $A_0 \approx 0{,}23 \text{ Bq}.$
- \begin{align*} A(2000) &\approx 0{,}23e^{-1{,}20968\cdot 10^{-4} \cdot 2000} \text{ Bq} \\ &\approx 0{,}18 \text{ Bq}. \end{align*}
- Noin 21,4 %.
Tämä on laskettu b-kohdan pyöristämättömällä tuloksella $0{,}180574477234\ldots \text{ Bq}$.
Eksponentiaalinen kasvu ja väheneminen
Elektronisessa laitteessa on sähkökatkosten varalta kondensaattori, jonka jännite turvaa laitteen muistissa olevat tiedot. Kun sähkökatkos alkaa, kondensaattori alkaa purkautua ja sen jännite $u(t)$ ajan funktiona pienenee yhtälön $$ u(t) = 12 \text{ V} \cdot e^{-0{,}1054t} $$ mukaisesti. (Tässä V tarkoittaa jännitteen yksikköä voltti.)
- Kuinka monta prosenttia kondensaattorin jännite pienenee sähkökatkoksen ensimmäisen tunnin aikana?
- Tiedetään, että tiedot säilyvät laitteen muistissa niin kauan kuin kondensaattorin jännite on vähintään 50 % sen jännitteestä sähkökatkoksen alussa. Piirrä kondensaattorin jännitettä kuvaavan funktion kuvaaja esimerkiksi Geogebralla. Tutki sen avulla graafisesti, kuinka pitkän sähkökatkoksen ajan kondensaattori pystyy turvaamaan laitteen muistissa olevat tiedot.
Vastaus
- Noin 10,0 %.
- Kuvaajasta voidaan lukea, että kondensaattorin jännite turvaa tiedot noin 6,5 tunnin sähkökatkoksen ajan:
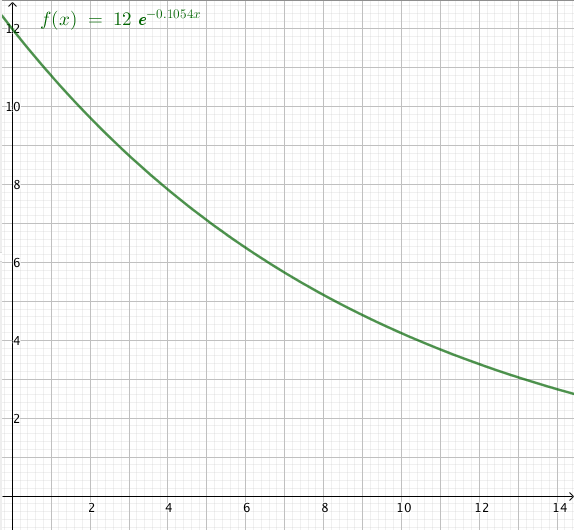
Luonnollinen logaritmi
- Määritä lukujen $e^9$ ja $\dfrac{1}{e^5}$ luonnolliset logaritmit.
- Minkä luvun luonnollinen logaritmi on $-0{,}5$? Anna vastauksena tarkka arvo, jos mahdollista.
Vastaus
- Luonnollisen logaritmin määritelmän mukaan \begin{align*} \ln (e^9) &= 9 \\[2mm] \ln \left(\dfrac{1}{e^5}\right) &= \ln (e^{-5}) = -5 \end{align*}
- Yhtälön $\ln x = -0{,}5$ ratkaisu on luonnollisen logaritmin määritelmän mukaan $$x = e^{-0{,}5} = \dfrac{1}{\sqrt{e}}.$$
Eksponenttifunktion derivaatta
Derivoi seuraavat funktiot:
- $f(x) = \dfrac{e^{3x} - 2}{e^x}$
- $g(x) = \left(e^x + e^{-x}\right)^2$
- $h(x) = e^{-\frac{1}{2}(5x+1)^4}$
Vastaus
- $f'(x) = \dfrac{2e^{3x} + 2}{e^x}$
- $g'(x) = 2(e^{2x} - e^{-2x}) =\dfrac{2(e^{4x} - 1)}{e^{2x}}$
- $h'(x) = -10(5x+1)^3e^{-\frac{1}{2}(5x+1)^4}$
Eksponenttifunktion derivaatta
Osoita, että funktio $$ f(x) = e^{-x} - x + 1 $$ on kaikkialla aidosti vähenevä.
Vastaus
Derivaattafunktion $$ f'(x) = -e^{-x} - 1 $$ arvot ovat kaikkialla negatiivisia. Nimittäin kaikilla $x \in \R$ pätee $e^{-x} > 0$ ja siten $$ f'(x) = -e^{-x} - 1 < 0 - 1 = -1. $$ Koska derivaattafunktion arvot ovat kaikkialla negatiivisia, on funktio $f$ kaikkialla aidosti vähenevä.
Eksponenttifunktion derivaatta
Osoita, että funktio $$ f(x) = xe^x + 1 $$ saa vain positiivisia arvoja.
Vastaus
Derivaattafunktiolla $$ f'(x) = xe^x + e^x $$ on yksi nollakohta $x = -1$. Kulkukaavion avulla nähdään, että funktio $f$ saa siinä pienimmän arvonsa. Tämä on $$ f(-1) = -e^{-1} + 1 \approx 0{,}63 > 0. $$ Koska funktion pienin arvo on positiivinen, ovat sen kaikki arvot positiivisia.
Eksponenttifunktion derivaatta
Osoita sopivan funktion kulkua tutkimalla, että
- yhtälöllä $e^x = 2x$ ei ole yhtään ratkaisua
- yhtälöllä $e^x = 3x$ on täsmälleen kaksi ratkaisua.
Vinkki: MAA6-kurssin teoreema 1 ja teoreema 10.
VASTAUS
- Funktion $f(x) = e^x - 2x$ derivaattafunktiolla $$f'(x) = e^x - 2$$ on tasan yksi nollakohta $x = \ln (2)$. Kulkukaaviosta nähdään, että funktio saa siinä pienimmän arvonsa. Koska pienin arvo on \begin{align*} f(\ln (2)) &= 2 - 2\ln(2) \\ &\approx 0{,}62 > 0, \end{align*} ovat funktion kaikki arvot positiivisia. Funktiolla ei siis ole nollakohtia eikä alkuperäisellä yhtälöllä ole ratkaisuja.
- Funktion $g(x) = e^x - 3x$ derivaattafunktiolla $$g'(x) = e^x - 3$$ on tasan yksi nollakohta $x = \ln (3)$. Kulkukaaviosta nähdään, että funktio saa siinä pienimmän arvonsa. Tämä on \begin{align*} g(\ln(3)) &= 3 - 3\ln(3) \\ &\approx -0{,}30 < 0. \end{align*} Lisäksi $$g(0) = 1 > 0$$ ja $$g(2) = e^2 - 6 \approx 1{,}4 > 0,$$ joten jatkuvalla funktiolla $g$ on Bolzanon lauseen mukaan ainakin yksi nollakohta välillä $\pa 0, \ln(3)\pe$ ja ainakin yksi nollakohta välillä $\pa \ln(3), 2\pe$ (MAA6, teoreema 1). Kulkukaavion mukaan $g$ on aidosti vähenevä välillä $\pa 0, \ln(3)\pe$ ja aidosti kasvava välillä $\pa \ln(3), 2\pe$, joten kummallakin välillä nollakohtia on enintään yksi.
Eksponenttifunktion derivaatta
Suorakulmion kaksi kärkeä on $x$-akselilla ja kaksi muuta käyrällä $$ y = e^{-\left|x\right|}. $$ Tehtävänä on määrittää tällaisen suorakulmion suurin mahdollinen pinta-ala.
- Piirrä tilanteesta kuva esimerkiksi Geogebralla.
- Muodosta funktio, joka ilmaisee suorakulmion pinta-alan.
- Mikä on suorakulmion suurin mahdollinen pinta-ala?
Vastaus
- Kuva:
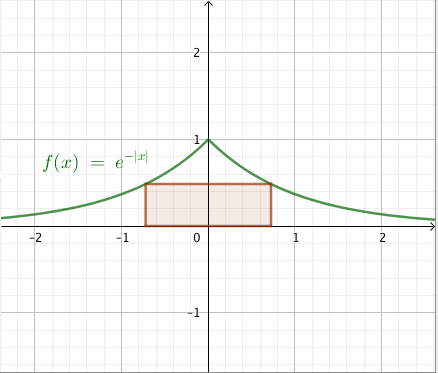
- $A(x) = 2xe^{-x}$, missä $x > 0$.
- Suurin mahdollinen pinta-ala on $$A(1) = 2e^{-1} \approx 0{,}736.$$ Se löydetään derivaattafunktion $$ A'(x) = (2-2x)e^{-x} $$ nollakohdasta. Kulkukaavion avulla voidaan varmistaa, että kysymyksessä todella on pienin arvo.
Eksponenttifunktion derivaatta
Oletetaan, että $a \neq 0$. Käyrälle $$ y = ae^{-\frac{1}{2}x^2} $$ piirretään tangentti kohtaan $x = 1$. Osoita, että tangentti leikkaa $x$-akselin samassa pisteessä vakion $a$ arvosta riippumatta. Mikä tämä leikkauspiste on?
Vastaus
Käyrälle piirretyn tangentin kulmakerroin on funktion $$ f(x) = ae^{-\frac{1}{2}x^2} $$ derivaattafunktion $$ f'(x) = -axe^{-\frac{1}{2}x^2} $$ arvo kohdassa $x = 1$: $$ f'(1) = -ae^{-\frac{1}{2}} = -\frac{a}{\sqrt{e}}. $$ Sivuamispiste on $(1, f(1)) = \left(1, \frac{a}{\sqrt{e}}\right)$, joten tangentin yhtälö on $$ y = -\frac{a}{\sqrt{e}} x + \frac{2a}{\sqrt{e}}. $$ Sen ja $x$-akselin leikkauspisteen $y$-koordinaatti on nolla. Yhtälön $$ -\frac{a}{\sqrt{e}} x + \frac{2a}{\sqrt{e}} = 0 $$ ratkaisuksi saadaan $x = 2$. Leikkauspiste on siis $(2,0)$.
Eksponenttifunktion derivaatta
Määritä funktion $$ f(x) = x^2e^{-x} $$ ääriarvot. Onko funktiolla suurinta tai pienintä arvoa?
Vastaus
Funktiolla on minimiarvo $f(0) = 0$ ja maksimiarvo $f(2) = 4e^{-2}$.
Derivaattafunktiolla $$ f'(x) = (2x-x^2)e^{-x} $$ on kaksi nollakohtaa: $x_1 = 0$ ja $x_2 = 2$. Kulkukaavion avulla saadaan selville, että $x_1 = 0$ on minimikohta ja $x_2 = 2$ on maksimikohta.
Tiedetään, että kaikilla $x \in \R$ pätee $x^2 \geq 0$ ja $e^{-x} > 0$, joten funktion $f$ arvot ovat aina epänegatiivisia. Siten $f(0) = 0$ on funktion $f$ pienin arvo.
Funktio $f$ on välillä $\pa -\infty, 0]$ aidosti vähenevä ja esimerkiksi $f(-2) = 4e^{2} \approx 29{,}6$ on suurempi kuin maksimiarvo $f(2)$, joten funktiolla $f$ ei ole suurinta arvoa.
Eksponenttifunktion derivaatta
Osoita, että $$ e^x \geq 1 + x $$ kaikilla reaaliluvuilla $x$.
Vastaus
Tutkitaan, onko erotusfunktiolla $$ f(x) = e^x - x - 1 $$ pienin arvo. Derivaattafunktiolla $$ f'(x) = e^x - 1 $$ on tasan yksi nollakohta $x = 0$. Kulkukaavion avulla nähdään, että funktio $f$ saa siinä pienimmän arvonsa. Pienin arvo on $$ f(0) = e^0 - 0 - 1 = 0, $$ joten $f(x) \geq 0$ kaikilla reaaliluvuilla $x$. Siis $$ e^x \geq 1 + x $$ kaikilla reaaliluvuilla $x$.
Eksponenttifunktion derivaatta
Määritä käyrien $$ y = (x^2 + 2x - 1)e^x $$ ja $$ y = -e^x $$ leikkauspisteet. Osoita, että yhdessä leikkauspisteessä käyrät leikkaavat toisensa kohtisuorasti.
Vastaus
Leikkauspisteet löydetään ratkaisemalla yhtälö $$ (x^2 + 2x - 1)e^x = -e^x. $$ Leikkauspisteet ovat $x_1 = 0$ ja $x_2 = -2$. Käyrät voidaan ajatella funktioiden $$ f(x) = (x^2 + 2x - 1)e^x $$ ja $$ g(x) = -e^x $$ kuvaajiksi. Derivaattafunktiot ovat $$ f'(x) = (x^2 + 4x + 1)e^x $$ ja $$ g'(x) = -e^x. $$ Kohdassa $x = 0$ käyrille piirrettyjen tangenttien kulmakertoimien tulo on $-1$, sillä $f'(0) = 1$ ja $g'(0) = -1$. Käyrät siis leikkaavat toisensa kohtisuorasti, koska niiden tangentit ovat kohtisuorassa toisiaan vastaan.
Eksponenttifunktion derivaatta
Käyrälle $y = e^x$ piirretään tangentti pisteeseen $P$. Lisäksi piirretään pisteen $P$ kautta kulkeva $y$-akselin suuntainen suora. Tehtävänä on osoittaa, että näiden kahden suoran $x$-akselista erottaman janan pituus ei riipu pisteen $P$ paikasta käyrällä.
- Piirrä tilanteesta mallikuva esimerkiksi Geogebralla.
- Merkitse pisteen $P$ $x$-koordinaattia jollakin kirjaimella. Mikä on tällöin sen $y$-koordinaatti?
- Määritä pisteen $P$ kautta kulkevan tangentin yhtälö. Missä pisteessä tangentti leikkaa $x$-akselin?
- Määritä pisteen $P$ kautta kulkevan $y$-akselin suuntaisen suoran yhtälö. Miten pitkän janan se erottaa $x$-akselista yhdessä tangentin kanssa?
Vastaus
- Kuva:
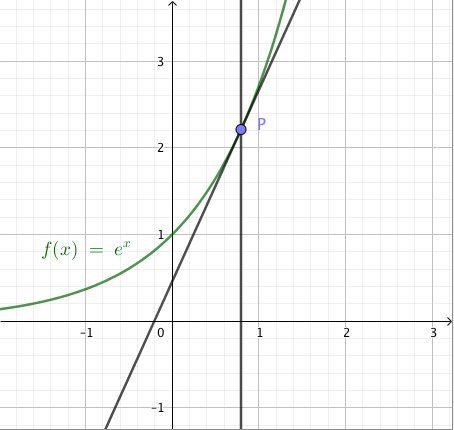
- Esimerkiksi $P = (a, e^a)$.
- Tangentin yhtälö on $$ y = e^ax + (1-a)e^a. $$ Se leikkaa $x$-akselin pisteessä $(a-1, 0)$.
- Pisteen $P$ kautta kulkevan $y$-akselin suuntaisen suoran yhtälö on $x = a$, joten se leikkaa $x$-akselin pisteessä $(a,0)$. Tämä suora ja tangentti erottavat $x$-akselista janan, jonka pituus on $a - (a-1) = 1$.
Eksponenttifunktion derivaatta
Määritä funktion $$ f(x) = e^{-x}\sin x $$ suurin ja pienin arvo välillä $\left[0, \frac{\pi}{2}\right]$.
Vinkki: MAA7-kurssin teoreemasta 16 voi olla apua yhtälönratkaisussa.
Vastaus
Derivaattafunktion $$ f'(x) = e^{-x}(\cos x - \sin x) $$ nollakohdat löydetään ratkaisemalla yhtälö $$ \cos x = \sin x. $$ MAA7-kurssin teoreeman 16 mukaan se voidaan kirjoittaa muodossa $$ \sin\left(x + \frac{\pi}{2}\right) = \sin x. $$ Ratkaisuiksi saadaan välivaiheiden jälkeen $$ x = \frac{\pi}{4} + n \cdot \pi, $$ missä $n$ on kokonaisluku. Suurin ja pienin arvo löytyvät nyt välin $\left[0, \frac{\pi}{2}\right]$ päätepisteistä tai sille osuvasta derivaatan nollakohdasta: \begin{align*} f(0) &= \sin 0 = 0 \\[2mm] f\left(\frac{\pi}{4}\right) &= e^{-\frac{\pi}{4}} \frac{1}{\sqrt{2}} \approx 0{,}322 \\[2mm] f\left(\frac{\pi}{2}\right) &= e^{-\frac{\pi}{2}} \approx 0{,}208. \end{align*} Funktion pienin arvo välillä $\left[0, \frac{\pi}{2}\right]$ on siis $f(0) = 0$ ja suurin arvo on $$ f\left(\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}e^{-\frac{\pi}{4}}. $$
Eksponenttifunktion derivaatta
Radioaktiivista jodia käytetään joissakin tilanteissa lääketieteellisenä hoitona. Tällöin on otettava huomioon, että potilas on hoidon aikana itsekin radioaktiivinen ja hänet on eristettävä ympäristöstä, jotta muut ihmiset eivät altistu haitalliselle säteilylle.
Potilaalle annettiin radiojodiannos, jonka aktiivisuus oli $3{,}0$ GBq eli $3{,}0 \cdot 10^9$ Bq. Jodin radioaktiivisen isotoopin jodi-131 puoliintumisaika on 8,0 vuorokautta, joten aktiivisuus puolittuu aina kahdeksan vuorokauden kuluessa.
- Muodosta funktio $A(t)$, joka ilmaisee aktiivisuuden $t$ vuorokauden kuluttua radiojodiannoksen antamisesta.
- Millä nopeudella aktiivisuus pienenee yhden vuorokauden kuluttua radiojodiannoksen antamisen jälkeen?
- Millä nopeudella aktiivisuus pienenee viikon kuluttua radiojodiannoksen antamisen jälkeen?
Vastaus
- Funktio on \begin{align*} A(t) &= 3 \text{ GBq} \cdot \left(\frac{1}{2}\right)^\frac{t}{8} \\[2mm] &= 3 \text{ GBq} \cdot e^{\ln\left(\frac{1}{2}\right)\cdot \frac{t}{8}} \end{align*}
- Derivaattafunktio on $$ A'(t) = 3 \text{ GBq} \cdot \ln\left(\frac{1}{2}\right) \cdot \frac{1}{8} e^{\ln\left(\frac{1}{2}\right)\cdot \frac{t}{8}}, $$ joten vuorokauden kuluttua $$ A'(1) \approx -0{,}24 \text{ GBq}. $$ Aktiivisuus siis pienenee noin $0{,}24 \text{ GBq}$ vuorokaudessa.
- Seitsemän vuorokauden kuluttua muutosnopeus on $$ A'(7) \approx -0{,}14 \text{ GBq}. $$ Aktiivisuus siis pienenee noin $0{,}14 \text{ GBq}$ vuorokaudessa.
Eksponenttifunktion derivaatta
Suora sivuaa funktion $$ f(x) = e^{\frac{1}{2}x^2} $$ kuvaajaa. Osoita, että suoran kulmakerroin on sivuamispisteen $x$- ja $y$-koordinaattien tulo.
Vastaus
Olkoon sivuamispisteen $x$-koordinaatti $a$, jolloin sivuamispiste on $$ \left(a, e^{\frac{1}{2}a^2}\right) $$ Suoran kulmakerroin on derivaatan arvo: $$ f'(a) = ae^{\frac{1}{2}a^2}. $$ Huomataan, että se on sama kuin sivuamispisteen $x$- ja $y$-koordinaattien tulo.
Eksponenttifunktion derivaatta
Funktion $$ f(x) = e^{-x^2} $$ kuvaajalle piirretään normaali pisteeseen $(a, f(a))$, missä $a \neq 0$. Mitä pistettä normaalin ja $y$-akselin leikkauspiste lähenee, kun $a$ lähenee nollaa?
Vastaus
Tangentin kulmakerroin on derivaatan arvo: $$ f'(a) = -2ae^{-a^2} $$ Tangentin ja normaalin kulmakertoimien tulo on $-1$, joten normaalin kulmakerroin on $$ \frac{e^{a^2}}{2a}. $$ Normaalin yhtälöksi saadaan $$ y = \frac{e^{a^2}}{2a} x - \frac{e^{a^2}}{2} + e^{-a^2}. $$ Normaalin ja $y$-akselin leikkauspisteessä $x = 0$, joten sen $y$-koordinaatti on $$ y = - \frac{e^{a^2}}{2} + e^{-a^2}. $$ Kun $a \rightarrow 0$, niin $$ y \rightarrow -\frac{1}{2} + 1 = \frac{1}{2}. $$ Leikkauspiste lähestyy siis pistettä $\left(0, \frac{1}{2}\right)$.
Eksponenttifunktion derivaatta
Millä vakion $a$ arvoilla funktio $$ g(x) = xe^{ax} + a $$ saa vain positiivisia arvoja?
Vastaus
Jos $a = 0$, funktio on $g(x) = x$. Tämä funktio saa myös negatiivisia arvoja, esim. $g(-1) = -1$.
Oletetaan, että $a \neq 0$. Tutkitaan funktion $g$ pienintä arvoa. Derivaattafunktiolla $$ g'(x) = (ax + 1)e^{ax} $$ on tasan yksi nollakohta $x = -\frac{1}{a}$. Lausekkeen $e^{ax}$ arvo on aina positiivinen, joten derivaatan arvo määräytyy lausekkeen $ax + 1$ arvon mukaan.
- Jos $a > 0$, $y = ax + 1$ on nouseva suora, eli derivaatan arvo on negatiivinen nollakohdan vasemmalla puolella ja positiivinen nollakohdan oikealla puolella. Derivaatan nollakohdassa funktio saa pienimmän arvonsa: $$ g\left(-\frac{1}{a}\right) = -\frac{1}{a}e^{-1} + a. $$ Tämä on positiivinen, jos ja vain jos \begin{align*} a &> \frac{1}{a}e^{-1} \\[2mm] a^2 &> \frac{1}{e} \\[2mm] (a < -\frac{1}{ \sqrt{e} } \text{ tai) } &a > \frac{1}{ \sqrt{e} } \end{align*} Huomaa, että epäyhtälön ratkaisussa käytettiin oletusta $a > 0$ kahdessa kohdassa.
- Jos $a < 0$, $y = ax + 1$ on laskeva suora, eli derivaatan arvo on positiivinen nollakohdan vasemmalla puolella ja negatiivinen nollakohdan oikealla puolella. Kokeilemalla huomataan, että esimerkiksi $g(0) = a < 0$. Tässä tilanteessa funktio saa siis negatiivisen arvon ainakin kohdassa $x = 0$.
Funktio $g$ saa siis vain positiivisia arvoja, jos ja vain jos $$ a > \frac{1}{\sqrt{e}}. $$
Eksponenttifunktion derivaatta
Määritä suoran $y = x$ se piste, jonka etäisyys käyrästä $y = e^x$ on pienin.
Vinkki: MAA5-kurssin teoreema 13.
Vastaus
Pisteen $(x, e^x)$ suorasta $x - y = 0$ on MAA5-kurssin teoreeman 13 mukaan \begin{align*} d(x) &= \frac{\left|x-e^x\right|}{\sqrt{2}} \\ &= \frac{1}{\sqrt{2}} (e^x - x). \end{align*} Itseisarvojen poistamiseen käytettiin tietoa, että $e^x > x$ kaikilla reaaliluvuilla $x$.
Etäisyysfunktion derivaattafunktio on $$ d'(x) = \frac{1}{\sqrt{2}} (e^x - 1). $$ Sillä on tasan yksi nollakohta $x = 0$. Kulkukaaviosta nähdään, että funktio $d$ saa siinä pienimmän arvonsa. Siis käyrän $y = e^x$ suoraa $y = x$ lähinnä oleva piste on $(0,e^0) = (0,1)$.
Käyrälle $y = e^x$ pisteeseen $(0,1)$ asetetun tangentin kulmakerroin on $e^0 = 1$, joten normaalin kulmakerroin on $-1$. Normaalin yhtälö on siten $$ y = -x + 1. $$ Normaalin ja suoran $y = x$ leikkauspiste on $\left(\frac{1}{2}, \frac{1}{2}\right)$. Tämä on etsitty piste.
Eksponenttifunktion derivaatta
Oletetaan, että $k > 0$ ja $k \neq 1$. Eksponenttifunktion $$ f(x) = k^x $$ kuvaajalle piirretään origon kautta kulkeva tangentti. Osoita, että sivuamispisteen $y$-koordinaatti ei riipu kantaluvusta $k$.
Vinkki: tehtävä 2.12 ja tehtävä 2.17 (a).
Vastaus
Olkoon sivuamispisteen $x$-koordinaatti $a$. Sivuamispiste on silloin $(a, k^a)$ ja tangentin kulmakerroin on $$ f'(a) = k^a\ln(k). $$ Koska tangentti kulkee origon kautta, sen yhtälö on $$ y = k^a\ln(k)x. $$ Sivuamispisteen koordinaatit toteuttavat tangentin yhtälön, joten saadaan yhtälö $$ k^a = k^a\ln(k)a. $$ Siitä saadaan ratkaistua $$ a = \frac{1}{\ln(k)}. $$ Sivuamispisteen $y$-koordinaatti on siten $$ k^a = e^{\ln(k)a} = e^{\ln(k)\frac{1}{\ln(k)}} = e^1 = e. $$
TEHTÄVÄSARJA III
Tiedetään, että $h(x) = g(f(x))$, $f(x) = e^x$ ja $g(x)=2x^2 + 1$. Elmeri ja Uolevi laskevat derivaatan h'(x) seuraavalla tavalla:
Elmerin ratkaisu: \begin{align*} f(x) &= e^x \\ g'(x) &= 4x \end{align*} joten $h'(x) = g'(f(x)) = 4e^x$
Uolevin ratkaisu: \begin{align*} h(x) &= g(f(x)) \\ &= 2(e^x)^2 + 1\\ &= 2e^{x^2} + 1 \\[1mm] h'(x) &= 2e^{x^2}\cdot (2x) \end{align*} joten $h'(x) = 4xe^{x^2}$.
Mari saa laskimella vastaukseksi $4e^{2x}$. Kenen vastaus on oikein? Etsi väärien ratkaisujen virheet ja esitä korjatut ratkaisut.
[Pitkä K2017/10]
Vastaus
Marin vastaus on oikein.
Elmerin ratkaisussa yhdistetyn funktion derivointisäännön mukaan \begin{align*} h'(x) &= g'(f(x))\cdot f'(x) \\ &= 4e^x\cdot e^x \\ &= 4(e^x)^2 = 4e^{2x}. \end{align*} Uolevin ratkaisussa yhdistetty funktio on \begin{align*} h(x) &= g(f(x)) \\ &= 2(e^x)^2 + 1 = 2e^{2x} + 1. \end{align*} Sen derivaatta on $$ h'(x) = 2e^{2x} \cdot 2 = 4e^{2x}. $$
- Pekka aloittaa kuumeen mittaamisen ajanhetkellä $t = 0$. Pekan käyttämän mittarin lukema $f(t)$ hetkellä $t$ minuuttia saadaan kaavasta $f(t) = 38 - 2e^{-0{,}6t}$ celsiusastetta. Kuinka kauan mittausta pitää jatkaa, jotta tulos poikkeaa enintään asteen kymmenesosan arvosta $38{,}0$ celsiusastetta? Anna vastaus minuutin tarkkuudella.
- Määritä lämpötilan muutosnopeus $f'(3)$. Anna vastaus yhden desimaalin tarkkuudella.
[Pitkä S2014/3]
Vastaus
- $t \geq \dfrac{\ln (20)}{0{,}6} \approx 5$ minuuttia.
- Noin 0,2 astetta minuutissa.
Oheisessa kuvassa on rakenteilla arkkitehti Eero Saarisen suunnittelema Gateway Arch Saint Louisissa USA:ssa. Se rakennettiin vuosina 1963-1965. Kaaren muotoa kuvaa yhtälö $$ y = -39f\left(\frac{x}{39}\right) + 231. $$ Tässä $f(t) = \frac{1}{2}\left(e^t + e^{-t}\right)$, $x$-akseli kulkee maan pinnalla kaaren tyvien kautta ja $y$-akseli on kaaren symmetria-akseli. Mittayksikkönä on metri.
- Määritä kaaren korkeus metrin tarkkuudella.
- Määritä kaaren leveys metrin tarkkuudella.
- Kuinka suuressa terävässä kulmassa kaari kohtaa maanpinnan? Anna vastaus asteen tarkkuudella.

[Pitkä S2014/9]
Vastaus
- Kaaren korkeus on noin 192 metriä.
- Kaaren leveys on noin 192 metriä.
- Kulma on noin $80^\circ$.
- Osoita, että funktio $$ f(x) = \frac{e^x}{1 + e^x} $$ on aidosti kasvava, kun $x \in \R$.
- Määritä funktion $f(x)$ raja-arvo, kun $x$ kasvaa rajatta.
- Päteekö kaikilla $x \geq 10$ epäyhtälö $f(x) \geq 0{,}999$?
[Pitkä S2014/11]
Vastaus
- Derivaattafunktion $$ f'(x) = \frac{e^x}{(1 + e^x)^2} $$ arvo on positiivinen kaikilla muuttujan $x$ arvoilla, joten funktio $f$ on aidosti kasvava koko lukusuoralla.
- Supistetaan lausekkeella $e^x$: \begin{align*} f(x) &= \frac{e^x}{1 + e^x} \\[2mm] &= \frac{1}{\frac{1}{e^x} + 1} \\[2mm] &\xrightarrow[x \rightarrow \infty]{} \frac{1}{0+1} = 1 \end{align*}
- Koska $$f(10) = 0{,}99995\ldots > 0{,}999$$ ja funktio $f$ on aidosti kasvava, niin epäyhtälö pätee.
Käyrien $y = 2e^{-x}$ ja $y = x^2e^{-x}$ väliin jäävään rajoitettuun alueeseen asetetaan $y$-akselin suuntainen jana oheisen kuvion mukaisesti. Määritä tämän janan suurin mahdollinen pituus. Anna vastauksena tarkka arvo ja kaksidesimaalinen likiarvo.
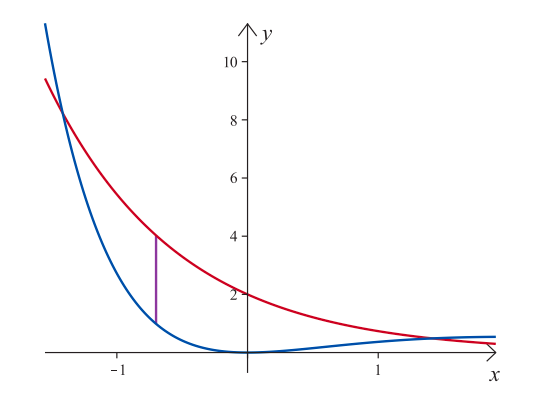
[Pitkä S2013/9]
Vastaus
Janan pituutta kuvaa funktio $$ f(x) = 2e^{-x} - x^2e^{-x}. $$ Sen suurin arvo on \begin{align*} f\left(1-\sqrt{3}\right) &= 2e^{\sqrt{3}-1}\left(\sqrt{3} - 1\right) \\ &\approx 3{,}04. \end{align*}
Määritä funktion $$ f(x) = (x^2-x-5)e^{-x} $$ suurin ja pienin arvo, kun $x \geq 0$.
[Pitkä K2013/5]
Vastaus
Funktion pienin arvo on $$f(0) = -5$$ ja suurin arvo on $$f(4) = \dfrac{7}{e^4}.$$
Eräässä huippuyliopistossa on 5 000 opiskelijaa, joista yksi sairastuu hiihtolomalta palattuaan influenssaan. Virus alkaa levitä kampuksella, ja siihen sairastuneiden opiskelijoiden lukumäärää kuvaa funktio $$ f(t) = \frac{5000}{1 + 4999e^{-0{,}8t}}, $$ jossa aika $t \geq 0$ lasketaan vuorokausina ensimmäisestä sairastumisesta alkaen.
- Luennot peruutetaan, jos yli 50 % opiskelijoista on sairaana. Kuinka monen vuorokauden kuluttua ensimmäisestä sairastumisesta näin tapahtuu?
- Näytä, että $f(t)$ on kasvava funktio, kun $t > 0$.
- Laske $$ \lim_{t \rightarrow \infty} f(t). $$ [Pitkä K2012/8]
Vastaus
- 11 vuorokauden kuluttua: $$ t > \frac{\ln (4999)}{0{,}8} \approx 10{,}6. $$
- Derivaattafunktio $$ f'(t) = \frac{19996000e^{-0{,}8t}}{(1 + 4999e^{-0{,}8t})^2} > 0, $$ joten funktio $f$ on aidosti kasvava.
- $$ \lim_{t \rightarrow \infty} f(t) = \frac{5000}{1 + 0} = 5000. $$
Tutki, kuinka monta ratkaisua yhtälöllä $$e^{x + a} = x$$ on vakion $a \in \R$ eri arvoilla.
[Pitkä S2012/10]
Vastaus
Yhtälön ratkaisujen määrä on sama kuin erotusfunktion $$f(x) = e^{x+a} −x$$ nollakohtien määrä. Funktion derivaatalla $$f'(x) = e^{x+a} − 1$$ on yksi nollakohta $x = −a$. Kun $x < −a$, on $f$ aidosti vähenevä ja kun $x > −a$ on $f$ aidosti kasvava. Funktion $f$ pienin arvo on $f(−a) = 1+a$. Tämän perusteella saadaan pääteltyä, että yhtälöllä
- ei ole ratkaisuja, jos $f(−a) > 0$ eli $a > −1$
- on yksi ratkaisu, jos $f(-a) = 0$ eli $a = -1$
- on kaksi ratkaisua, jos $f(-a) < 0$ eli $a < -1$.
Millä vakion $a$ arvoilla funktio $$ f(x) = e^x - a\left|x-1\right| $$ on kaikkialla kasvava?
[Pitkä K2008/10]
Vastaus
Funktio $f$ on kaikkialla jatkuva. Tarkastellaan erikseen tilanteet, joissa itseisarvojen sisällä oleva lauseke on positiivinen tai negatiivinen.
- Jos $x > 1$, niin $$ f(x) = e^x - a(x-1) $$ ja derivaattafunktio on $$ f'(x) = e^x - a. $$ Derivaattafunktio on siis positiivinen tai nolla, jos ja vain jos $e^x \geq a$. Koska eksponenttifunktio on aidosti kasvava, tämä epäyhtälö toteutuu tarkasteltavalla välillä $\pa 1, \infty\pe$, jos ja vain jos $e^1 \geq a$ eli $a \leq e$.
- Jos $x < 1$, niin $$ f(x) = e^x - a(1-x) $$ ja derivaattafunktio on $$ f'(x) = e^x + a. $$ Derivaattafunktio on siis positiivinen tai nolla, jos ja vain jos $e^x \geq -a$. Koska eksponenttifunktion arvot ovat positiivisia mutta lähenevät nollaa muuttujan arvon pienentyessä rajatta, tämä epäyhtälö toteutuu tarkasteltavalla välillä $\pa -\infty, 1\pe$, jos ja vain jos $-a \leq 0$ eli $a \geq 0$.
Jos siis $0 \leq a \leq e$, on jatkuva funktio $f$ kasvava sekä välillä $\pa -\infty, 1\pe$ että välillä $\pa 1, \infty\pe$, jolloin se on kasvava kaikkialla.
- Sievennä lauseke $$e^{2\ln x} - 2x^2.$$
- Laske funktion $$f(x) = 4e^{2x}$$ derivaatta kohdassa $x = 0$.
[Pitkä K2007/2c & K2012/2f]
Vastaus
- Logaritmin laskusääntöjen ja määritelmän avulla saadaan \begin{align*} e^{2\ln x} - 2x^2 &= e^{\ln(x^2)} - 2x^2 \\ &= x^2 - 2x^2 = -x^2 \end{align*}
- $f'(x) = 8e^{2x}$, joten $f'(0) = 8$.
- Ratkaise yhtälö $$ \left(e^x\right)^3 = e^{x^2} $$
- Funktion $$ f(x) = ax^2e^x + bxe^x $$ derivaatta on $$ f'(x) = 2x^2e^x + xe^x - 3e^x. $$ Määritä $a$ ja $b$.
[Pitkä K2009/2b & S2009/3a]
Vastaus
- Yhtälö toteutuu, jos ja vain jos $x = 0$ tai $x = 3$.
- $a = 2$ ja $b = -3$.
Olkoon $x \geq 1$. Osoita, että $$ x^x - e^{x - 1} \geq 0. $$ Millä muuttujan $x$ arvoilla pätee yhtäsuuruus?
[Pitkä K2004/11]
Vastaus
Epäyhtälön vasen puoli voidaan kirjoittaa muodossa $e^{x\ln x} - e^{x-1}$. Koska eksponenttifunktio on aidosti kasvava, on $$e^{x\ln x} - e^{x-1} \geq 0,$$ jos ja vain jos $$x\ln x \geq x - 1.$$ Tutkitaan erotusfunktiota $$ g(x) = x\ln x - x + 1. $$ Sen derivaattafunktioksi saadaan $$ g'(x) = \ln x. $$ Oletuksen mukaan $x \geq 1$. Jos $x > 1$, niin $g'(x) = \ln x > 0$. Lisäksi $g'(1) = 0$, joten funktio $g$ on aidosti kasvava välillä $[1, \infty\pe$. Pienimmän arvonsa se saa välin vasemmassa päätepisteessä: $$ g(1) = 0. $$ Tästä voidaan päätellä, että $g(x) \geq 0$ eli $$x\ln x \geq x - 1$$ kaikilla $x \geq 1$. Lisäksi yhtäsuuruus pätee, jos ja vain jos $x = 1$.
- Derivoi funktio $$f(x) = e^{2x-2} + x^3 -1.$$
- Määritä käyrän $$y = e^{2x-2} + x^3 -1$$ pisteeseen $(1,1)$ piirretyn tangentin yhtälö.
- Määritä sen janan pituus, jonka koordinaattiakselit erottavat edellisen kohdan tangentista.
[Pitkä S2003/3]
Vastaus
- $f'(x) = 2e^{2x-2} + 3x^2$
- Koska $f'(1) = 5$, saadaan pisteeseen $(1,1)$ piirretyn tangentin yhtälöksi $y = 5x-4$.
- Tangentti leikkaa akseleita pisteissä $(0,-4)$ ja $\left(\frac{4}{5},0\right)$. Niiden välisen janan pituus on $\frac{4}{5}\sqrt{26}$.
Funktiolla $$ f(x) = Ae^x + 2Be^{-x} $$ on ominaisuudet $f(0) = 1$ ja $f'(0) = 2$. Määritä kertoimet $A$ ja $B$.
Vastaus
Derivaatta on $$ f'(x) = Ae^x - 2Be^{-x}. $$ Ehdoista saadaan yhtälöpari $A + 2B = 1$ ja $A - 2B = 2$. Sen ratkaisu on $A = \frac{3}{2}$ ja $B = -\frac{1}{4}$.
Reaalilukujen joukossa määritellyn funktion $f$ kuvaajan pisteenseen $(x,y)$ piirretyn tangentin kulmakerroin on $$ k(x) = 1 - e^{-2x}. $$ Funktion pienin arvo on $2$. Määritä funktio $f$.
Vastaus
Kokeilemalla huomataan, että funktio on muotoa $$ f(x) = x + \frac{1}{2}e^{-2x} + C, $$ missä $C$ on mikä tahansa reaalilukuvakio. (Tällöin $f'(x) = k(x)$ kuten pitääkin.)
Derivaattafunktiolla $k$ on yksi nollakohta $x = 0$. Kulkukaaviosta nähdään, että funktio $f$ saa siinä pienimmän arvonsa. Yhtälöstä $f(0) = 2$ saadaan ratkaistua $C = 1{,}5$. Siis $$ f(x) = x + \frac{1}{2}e^{-2x} + \frac{3}{2}. $$
Olkoon $$ f(x) = e^{-x} + 1, $$ missä $x \in [1,2]$. Osoita, että $$ 1 < f(x) < 2 \ \text{ ja } \ \left|f'(x) \right| < 0{,}4. $$ Tiedetään, että tällöin yhtälö $x = f(x)$ voidaan ratkaista numeerisesti muodostamalla yhtälön ratkaisua kohden suppeneva jono $x_0$, $x_1$, $x_2$, $x_3, \ldots$ seuraavalla tavalla: valitaan jokin $x_0 \in [1,2]$ ja määritellään $x_n = f(x_{n-1})$, kun $n = 1, 2, 3, \ldots$. Määritä tällä tavoin yhtälön ratkaisu neljän merkitsevän numeron tarkkuudella lähtemällä arvosta $x_0 = 1{,}3$. Ilmoita laskemasi jonon termit.
Vastaus
Derivaattafunktion $f'(x) = -e^{-x}$ arvot ovat aina negatiivisia, joten $f$ on aidosti vähenevä. Funktion suurin arvo välillä $[1,2]$ on siten $f(1) = e^{-1} + 1 < 2$ ja pienin arvo $f(2) = e^{-2} + 1 > 1$. Siis $1 < f(x) < 2$ kaikilla $x \in [1,2]$.
Toisen derivaatan $f''(x) = e^{-x}$ arvot ovat aina positiivisia, joten derivaattafunktio $f'$ on aidosti kasvava. Derivaattafunktion arvot ovat aina negatiivisia, joten se saa itseisarvoltaan suurimman arvon välillä $[1,2]$ kohdassa $x = 1$: $$\left|f'(1)\right| = \left|-e^{-1}\right| < 0{,}4.$$
Etsitty ratkaisu on $x \approx 1{,}278$.
- Derivoi lauseke $$ (x^2 + 1)e^{2x}. $$
- Olkoon $$f(x) = 2^{-x}.$$ Laske $f'(1)$.
[Pitkä S2006/2a & S2011/2c]
Vastaus
- $2(x^2 + x + 1)e^{2x}$
- $f'(x) = -2^{-x}\ln(2)$, joten $f'(1) = -\dfrac{1}{2}\ln(2)$.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

