Suorat ja tasot
Luvun tavoitteet
Tämän luvun tavoitteena on, että osaat esittää suoria ja tasoja vektorien avulla sekä tutkia niiden ominaisuuksia. Osaat
- muodostaa suoralle ja tasolle sekä vektorimuotoisen että koordinaattimuotoisen parametriesityksen
- tutkia, onko annettu piste tietyllä suoralla tai tietyssä tasossa
- määrittää kahden suoran leikkauspisteen sekä suoran ja tason leikkauspisteen
- laskea kahden suoran välisen kulman sekä suoran ja tason välisen kulman
- laskea pisteen etäisyyden suorasta ja tasosta
- muodostaa $xy$-koordinaatiston suoralle ja $xyz$-koordinaatiston tasolle normaalimuotoisen yhtälön.
Tavoitteiden toteutumista pääset arvioimaan luvun lopussa olevan itsearviointitestin avulla
Suora
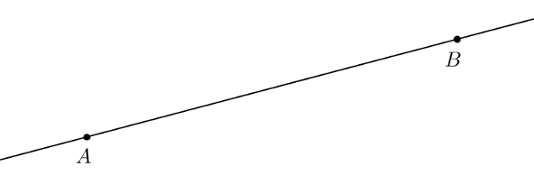
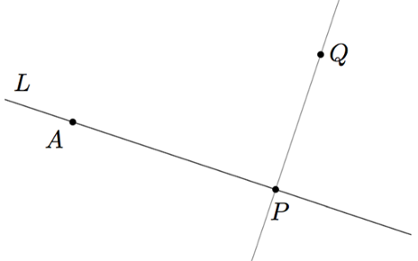
Tarkastellaan alla olevaa kuvaa. Sen pisteiden $A$ ja $B$ kautta on mahdollista piirtää ainoastaan yksi suora — pisteet $A$ ja $B$ määräävät suoran yksiselitteisesti.
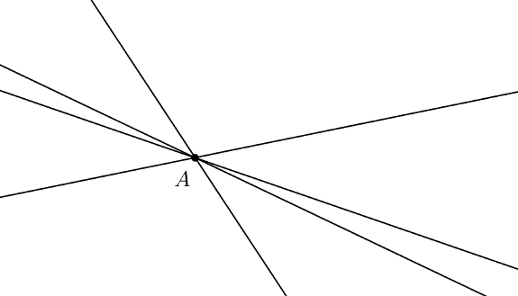
Yksi piste ei riitä, sillä sen kautta voi kulkea äärettömän monta eri suoraa.
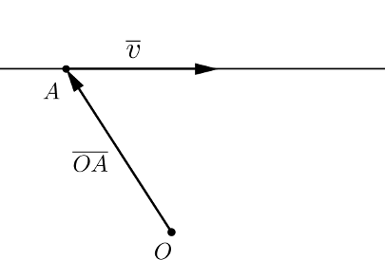
Suora voidaan määrittää vektoreiden avulla. Tällöin tarvitaan yhden suoran pisteen paikkavektori sekä yksi suoran suuntainen vektori. Tätä vektoria kutsutaan suoran suuntavektoriksi. Näitä on havainnollistettu alla olevassa kuvassa.
Suora
Tutki pisteiden $A=(-1,2)$ ja $B=(1,1)$ kautta kulkevaa suoraa $L$.
- Piirrä koordinaatistoon pisteet $A$ ja $B$ sekä suora $L$.
- Ilmaise vektorit $\pv{OA}$ ja $\pv{AB}$ vektoreiden $\vi$ ja $\vj$ avulla.
- Laske vektorit $\pv{OQ} = \pv{OA} + 2\pv{AB}$ ja $\pv{OR} = \pv{OA} - \pv{AB}$.
- Merkitse piirrokseesi vektorit $\pv{OA}$, $\pv{AB}$, $\pv{OQ}$ ja $\pv{OR}$.
- Merkitse piirrokseesi piste $S = (5,-1)$. Etsi sellainen luku $t$, että yhtälö $\pv{OS} = \pv{OA} + t\pv{AB}$ toteutuu.
- Merkitse piirrokseesi piste $C = (3,2)$. Onko mahdollista löytää sellainen luku $t$, että yhtälö $\pv{OC} = \pv{OA} + t\pv{AB}$ toteutuu? Selitä omin sanoin.
VASTAUS
- $\pv{OA} = -\vi + 2\vj\ $ ja $\ \pv{AB} = 2\vi - \vj$.
- $\pv{OQ} = 3\vi\ $ ja $\ \pv{OR} = -3\vi + 3\vj$.
- $t = 3$.
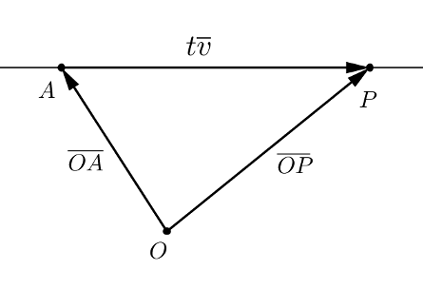
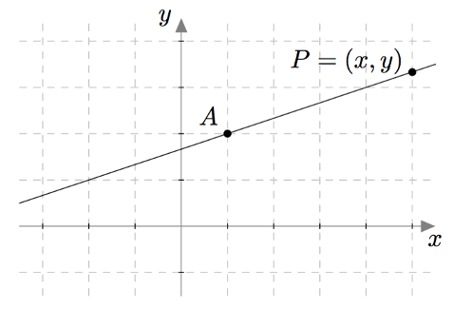
Edellisessä tehtävässä tarkasteltiin suoraa $L$, joka kulkee pisteen $A$ kautta ja jonka suuntavektori on $\vv = \pv{AB}.$ Tehtävässä havaittiin, että piste $P$ on suoralla $L$, jos ja vain jos on olemassa sellainen luku $t$, että $$\pv{OP} = \pv{OA} + t\vv.$$
MÄÄRITELMÄ: SUORAN VEKTORIMUOTOINEN PARAMETRIESITYS
Oletetaan, että $A$ on suoran $L$ piste ja $\vv$ on suoran $L$ suuntavektori. Yhtälö $$\pv{OP} = \pv{OA} + t\vv$$ on suoran $L$ vektorimuotoinen parametriesitys.
Tässä esiintyvä kerroin $t$ on parametri ja vektori $\pv{OA}$ on suoran paikkavektori.

Suoran vektorimuotoinen parametriesitys kertoo, millaisia suoran pisteiden paikkavektorit ovat. Antamalla parametrille $t$ eri arvoja, saadaan suoran eri pisteiden paikkavektoreita.
Suoran vektorimuotoinen parametriesitys
Tarkastele tätä Geogebra-sovellusta. Siinä on näkyvissä suora, jonka vektorimuotoinen parametriesitys on $$\pv{OP} = \pv{OA} + t\vv.$$ Säädä parametrin $t$ arvoa liukukytkimellä ja selvitä silmämääräisesti arvioiden,
- mikä on suoran paikkavektori $\pv{OA}$
- mikä on suoran suuntavektori $\vv$
- millä parametrin $t$ arvolla suoran vektorimuotoinen parametriesitys antaa suoran pisteen $P = (-1,2)$ paikkavektorin
- minkä suoran pisteen paikkavektori saadaan parametrin arvolla $t=3{,}7$.
Suoran vektorimuotoisen parametriesityksen avulla voidaan määrittää sekä tason että avaruuden suoria. Samaa suoraa voidaan kuvata usealla erilaisella parametriesityksellä, sillä suoran paikkavektoriksi voidaan valita suoran minkä tahansa pisteen paikkavektori ja suoran suuntavektoriksi voidaan valita mikä tahansa suoran suuntainen vektori.
Suoran vektorimuotoinen parametriesitys
Suoran $L$ vektorimuotoinen parametriesitys on $\pv{OP} = -2\vi + \vj + t(3\vi + 2\vj)$. Päättele parametriesityksen avulla suoralle $L$
- yksi paikkavektori
- yksi suuntavektori.
- Piirrä suora $L$ koordinaatistoon.
VASTAUS
- Esimerkiksi $-2\vi + \vj$.
- Esimerkiksi $3\vi + 2\vj$.
Suoran vektorimuotoinen parametriesitys
Tarkastele alla olevan kuvan suoraa $L$.
- Valitse suoralta $L$ yksi piste ja muodosta sen paikkavektori.
- Muodosta jokin suoran $L$ suuntavektori.
- Kirjoita näkyviin suoran $L$ vektorimuotoinen parametriesitys.
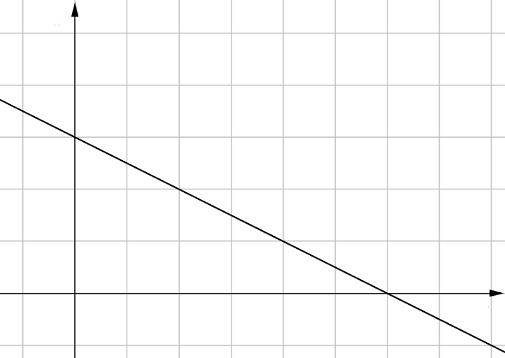
Alla olevassa kuvassa on suora, jonka vektorimuotoinen parametriesitys on $$\pv{OP} = \vi + 2\vj + t(3\vi + \vj).$$
Jos pisteen $P$ koordinaatteja merkitään kirjaimilla $x$ ja $y$, voidaan yllä oleva parametriesitys kirjoittaa muodossa $$x\vi + y\vj = \vi + 2\vj + t(3\vi + \vj).$$ Tämän yhtälön oikealla puolella voidaan kertoa sulut auki, jolloin yhtälö saadaan muotoon $$x\vi + y\vj = \vi + 2\vj + 3t\vi + t\vj.$$ Yhtälön oikeaa puolta voidaan vielä sieventää suorittamalla yhteenlaskut, minkä jälkeen yhtälö näyttää tältä: $$x\vi + y\vj = (1+3t)\vi + (2+t)\vj.$$ Vektoreiden samuuden määritelmän mukaan tämä yhtälö toteutuu, jos ja vain jos yhtälön eri puolilla olevat vektorit voidaan ilmaista samalla tavalla vektoreiden $\vi$ ja $\vj$ avulla eli $$ \left\{\begin{aligned} x &= 1+3t \\ y &= 2+t. \end{aligned}\right. $$ Minkä tahansa suoran vektorimuotoinen parametriesitys voidaan muuttaa vastaavaan muotoon, jossa suoran pisteen jokaiselle koordinaatille on oma yhtälönsä. Tätä esitystapaa sanotaan suoran koordinaattimuotoiseksi parametriesitykseksi.
Suoran koordinaattimuotoinen parametriesitys
Avaruuden suora $L$ kulkee pisteiden $A = (4,-1,3)$ ja $B = (2,1,3)$ kautta. Koska kysymyksessä on avaruuden suora, tarkan kuvan piirtäminen on hankalaa. Tilannetta voi kuitenkin havainnollistaa mallikuvalla:
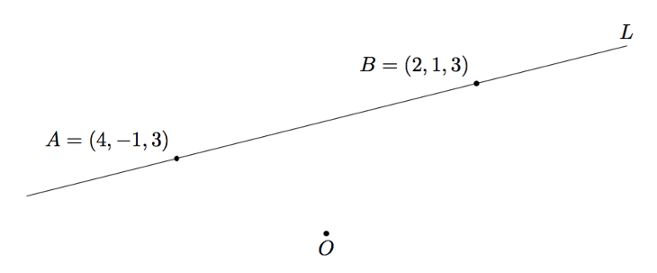
- Piirrä tilanteesta mallikuva omaan vihkoosi.
- Muodosta suoran $L$ jonkin pisteen paikkavektori ja jokin suoran $L$ suuntavektori. Merkitse nämä mallikuvaan.
- Muodosta suoran $L$ vektorimuotoinen parametriesitys.
- Määritä vektorimuotoisen parametriesityksen avulla kolme uutta pistettä suoralta $L$ antamalla eri arvoja parametrille $t$. Havainnollista näitä pisteitä mallikuvasi avulla.
- Muodosta suoran $L$ koordinaattimuotoinen parametriesitys c-kohdan avulla.
Suoran vektorimuotoisen parametriesityksen ja siitä saatavan koordinaattimuotoisen parametriesityksen avulla voidaan tutkia, onko jokin piste suoralla. Jos tarkastellun pisteen paikkavektori ei toteuta suoran parametriesitystä millään parametrin $t$ arvolla, voidaan päätellä, että tämä piste ei ole suoralla.
Onko piste suoralla?
Suoran $L$ koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 1-t \\ y &= -2+t \\ z &= 4t. \end{aligned}\right. $$
- Määritä suoralta $L$ kaksi pistettä antamalla parametrille $t$ kaksi eri arvoa.
- Tutki, onko piste $R=(4,-5,-12)$ suoralla $L$.
VASTAUS
- Kyllä, sillä parametrin arvolla $t = -3$ saadaan parametriesityksestä piste $R$.
Onko piste suoralla?
Suora $L$ kulkee pisteen $A = (1,4,-2)$ kautta ja sillä on suuntavektori $\vv = \vi - 2\vj + 3\vk$.
- Muodosta pisteen $Q = (-1,8,-8)$ paikkavektori ja tutki, onko yhtälöllä $\pv{OQ} = \pv{OA} + t\vv$ ratkaisua.
- Päättele a-kohdan avulla, onko piste $Q$ suoralla $L$. Selitä omin sanoin. Voit havainnollistaa tilannetta mallikuvalla.
- Tutki samaan tapaan, onko piste $R = (3,0,6)$ suoralla $L$. Voit havainnollistaa tilannetta mallikuvalla.
VASTAUS
- Yhtälöllä on ratkaisu $t = -2$.
- Piste $Q$ on suoralla $L$.
- Piste $R$ ei ole suoralla $L$.
Suoran koordinaattimuotoisesta parametriesityksestä voidaan tarvittaessa siirtyä takaisin vektorimuotoiseen parametriesitykseen, kuten seuraavassa tehtävässä tehdään.
Suoran vektorimuotoinen parametriesitys
Tehtävänä on muodostaa suoran $L$ vektorimuotoinen parametriesitys, kun tiedetään, että sen koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 2-2t \\ y &= 5+t \\ z &= 1 + 4t \end{aligned}\right. $$
- Määritä parametrin $t$ arvoa $t = 0$ vastaava suoran $L$ piste ja muodosta sen paikkavektori.
- Selitä, miten voit lukea a-kohdan paikkavektorin koordinaattimuotoisesta parametriesityksestä ilman laskuja.
- Miten voisit lukea suoran suuntavektorin koordinaattimuotoisesta parametriesityksestä ilman laskuja?
- Olkoon $A$ arvoa $t = 0$ vastaava suoran piste ja $B$ arvoa $t = 1$ vastaava suoran piste. Määritä nämä pisteet ja muodosta niiden avulla vektori $\pv{AB}$. Se on yksi suoran $L$ suuntavektori. Saitko saman tuloksen kuin c-kohdassa päättelemällä?
- Muodosta suoran $L$ vektorimuotoinen parametriesitys.
VASTAUS
- Piste on $(2,5,1)$ ja sen paikkavektori on $2\vi + 5\vj + \vk$.
- $\pv{AB} = -2\vi + \vj + 4\vk$
- Esimerkiksi $\pv{OP} = 2\vi + 5\vj + \vk + t(-2\vi + \vj + 4\vk)$
Tutkitaan seuraavaksi suorien leikkauspisteitä. Kaksi suoraa leikkaa toisensa, jos ja vain jos niillä on yhteinen piste. Toisin sanottuna kaksi suoraa leikkaa toisensa, jos ja vain jos on olemassa sellainen piste $P$, jonka paikkavektori $\pv{OP}$ saadaan kummankin suoran parametriesityksestä joillakin parametrien arvoilla. Tätä on havainnollistettu alla olevassa kuvassa.
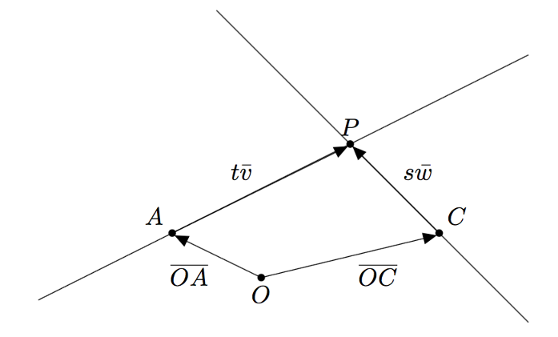
Suorien leikkauspiste
Suoran $L_1$ vektorimuotoinen parametriesitys on $\pv{OP} = -2\vi + 2\vj + t(\vi + 3\vj)$. Suoran $L_2$ vektorimuotoinen parametriesitys on $\pv{OP} = 2\vi - \vj + s(-2\vi - \vj)$.
- Piirrä kumpikin suora koordinaatistoon. Merkitse kuvaan suorien paikkavektorit ja suuntavektorit.
- Suorilla on yksi leikkauspiste $P$. Määritä sen koordinaatit piirroksesi avulla.
- Päättele piirroksesi avulla, millä parametrin $t$ arvolla leikkauspisteen paikkavektori $\pv{OP}$ saadaan suoran $L_1$ parametriesityksestä.
- Päättele piirroksesi avulla, millä parametrin $s$ arvolla leikkauspisteen paikkavektori $\pv{OP}$ saadaan suoran $L_2$ parametriesityksestä.
VASTAUS
- $P = (-4,-4)$
- $t = -2$
- $s = 3$
Tarkastellaan suoria, joiden vektorimuotoiset parametriesitykset ovat $\pv{OP} = \pv{OA} + t\vv$ ja $\pv{OP} = \pv{OC} + s\vw$. Jos näillä suorilla on leikkauspiste, sen paikkavektori saadaan näistä parametriesityksistä joillakin parametrien $t$ ja $s$ arvoilla. Leikkauspiste löydetään siis tutkimalla yhtälöä $$\pv{OA} + t\vv = \pv{OC} + s\vw.$$ Jos tällä yhtälöllä ei ole ratkaisua, tarkoittaa se, ettei suorilla ole yhtään leikkauspistettä.
Esimerkiksi edellisen tehtävän suorien $L_1$ ja $L_2$ leikkauspiste löydetään tutkimalla yhtälöä $$-2\vi + 2\vj + t(\vi + 3\vj) = 2\vi - 1\vj + s(-2\vi - \vj).$$ Kertomalla sulut auki se saadaan muotoon $$-2\vi + 2\vj + t\vi + 3t\vj = 2\vi - 1\vj + -2s\vi - s\vj.$$ Vasenta ja oikeaa puolta voidaan vielä sieventää suorittamalla yhteenlaskut, jolloin päästään yhtälöön $$(-2+t)\vi + (2+3t)\vj= (2-2s)\vi +(-1-s)\vj.$$ Vektoreiden samuuden määritelmän mukaan tämä yhtälö toteutuu, jos ja vain jos yhtälön eri puolilla olevat vektorit voidaan ilmaista samalla tavalla vektoreiden $\vi$ ja $\vj$ avulla eli $$ \left\{\begin{aligned} -2+t &= 2-2s \\ 2+3t &= -1-s. \end{aligned}\right. $$ Lisäämällä ensimmäisen yhtälön molemmille puolille $2+2s$ ja toisen yhtälön molemmille puolille $s-2$ saadaan yhtälöryhmä muotoon $$ \left\{\begin{aligned} 2s+t &= 4 \\ s+3t &= -3. \end{aligned}\right. $$ Tämä yhtälöpari voidaan ratkaista samaan tapaan kuin edellisessä luvussa tehtiin.
Suorien leikkauspiste
Ratkaise yhtälöpari $$ \left\{\begin{aligned} 2s+t &= 4 \\ s+3t &= -3. \end{aligned}\right. $$ ja vertaa tulosta edellisen tehtävän tulokseen. Saitko laskemalla saman tuloksen kuin kuvasta päättelemällä?
Suorien leikkauspiste
Suoran $L_1$ vektorimuotoinen parametriesitys on $\pv{OP}=\vi-2\vk+t(2\vi+\vj+4\vk)$ ja suoran $L_2$ koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 3-s \\ y &= 1+s\\ z &= 2+s. \end{aligned}\right. $$
- Lausu suoran $L_1$ vektorimuotoinen parametriesitys koordinaattimuotoisena parametriesityksenä.
- Tutki, leikkaavatko suorat $L_1$ ja $L_2$ toisensa. Mitkä ovat mahdollisen leikkauspisteen koordinaatit?
VASTAUS
- Koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 1 + 2t \\ y &= t\\ z &= -2+4t. \end{aligned}\right. $$
- Leikkauspiste on $(3,1,2)$.
Suorien leikkauspiste
Suora $L_1$ kulkee pisteiden $A = (4;4;-4{,}5)$ ja $B = (5,6,-7)$ kautta. Suora $L_2$ kulkee pisteiden $C = (5,0,-1)$ ja $D = (7,1,-3)$ kautta.
- Harjoittele Geogebran käyttöä piirtämällä sen avulla tilanteesta kaksiulotteinen mallikuva. Katso tarvittaessa mallia tästä videosta.
- Muodosta suoran $L_1$ vektorimuotoinen parametriesitys.
- Muodosta suoran $L_2$ vektorimuotoinen parametriesitys. Käytä parametrina jotain toista kirjainta kuin a-kohdassa.
- Tutki, leikkaavatko suorat $L_1$ ja $L_2$ toisensa. Mitkä ovat mahdollisen leikkauspisteen koordinaatit?
- Harjoittele Geogebran käyttöä piirtämällä sen avulla tilanteesta tarkka kolmiulotteinen kuva, jota voit käyttää myös d-kohdan vastauksen tarkistamiseen. Katso tarvittaessa mallia tästä videosta.
VASTAUS
- Suorat leikkaavat toisensa, leikkauspiste on $(1, -2, 3)$.
Suorien leikkauspiste
Suora $L_1$ kulkee pisteiden $A = (1,-3,0)$ ja $B = (4,0,3)$ kautta. Suora $L_2$ kulkee pisteiden $C = (5,2,2)$ ja $D = (8,0,1)$ kautta.
- Muodosta suoran $L_1$ vektorimuotoinen parametriesitys.
- Muodosta suoran $L_2$ vektorimuotoinen parametriesitys. Käytä parametrina jotain toista kirjainta kuin a-kohdassa.
- Tutki, leikkaavatko suorat $L_1$ ja $L_2$ toisensa. Mitkä ovat mahdollisen leikkauspisteen koordinaatit?
VASTAUS
- Suorat eivät leikkaa toisiaan.
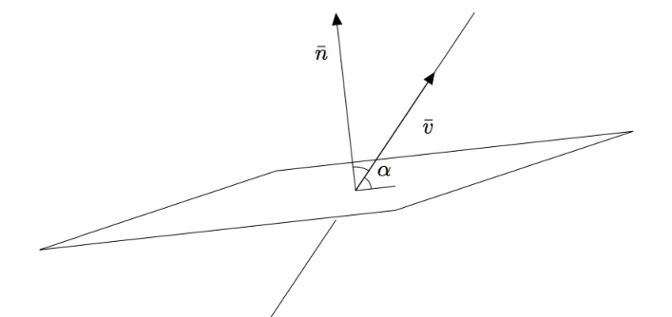
MÄÄRITELMÄ: SUORIEN VÄLINEN KULMA
Suorien välinen kulma tarkoittaa toisensa leikkaavien suorien muodostamista kulmista sitä, joka on terävä tai suora kulma. Esimerkiksi alla olevan kuvan suorien välinen kulma on $\alpha$.
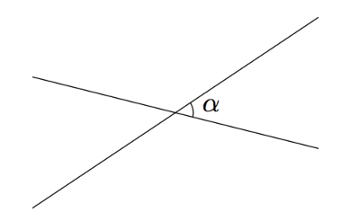
Jos suorat eivät leikkaa toisiaan, tarkoittaa suorien välinen kulma näiden suorien kanssa yhdensuuntaisten toisensa leikkaavien suorien välistä kulmaa.
Kahden suoran välistä kulmaa voidaan tutkia pistetulon avulla. Esimerkiksi alla olevassa kuvassa suoran $L_1$ suuntavektoriksi voidaan valita vektori $\vv = -3\vi + 2\vj$ ja suoran $L_2$ suuntavektoriksi voidaan valita $\vw = 4\vi + 3\vj$.
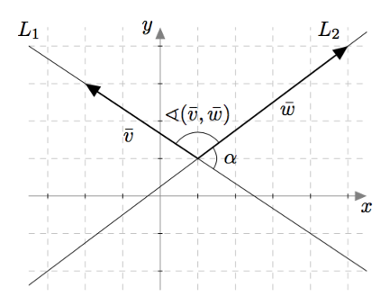
Suuntavektoreiden $\vv$ ja $\vw$ välisen kulman kosini saadaan yhtälöstä $$ \begin{align*} \cos(\vv, \vw) &= \frac{\vv \cdot \vw}{|\vv||\vw|} \\ &= \frac{-3\cdot 4 + 2\cdot 3}{\sqrt{(-3)^2 + 2^2}\sqrt{4^2 + 3^2}} \\ &= \frac{-6}{\sqrt{13}\cdot 5} \\ &\approx -0{,}332820. \end{align*} $$ Tästä saadaan laskimella $\sphericalangle(\vv, \vw) = 109{,}44003\ldots \approx 109{,}4^\circ$. Koska tulos on yli $90^\circ$ eli kulma on tylppä, voidaan päätellä, että suorien $L_1$ ja $L_2$ välinen kulma on $\alpha = 180^\circ - \sphericalangle(\vv, \vw) \approx 180^\circ - 109{,}4^\circ = 70{,}6^\circ$.
Suorien välinen kulma
- Laske tehtävän 3.13 suorien $L_1$ ja $L_2$ välinen kulma asteen kymmenesosan tarkkuudella.
- Miten on mahdollista, että suorat $L_1$ ja $L_2$ eivät leikkaa toisiaan, vaikka ne eivät ole yhdensuuntaisia? Selitä omin sanoin.
VASTAUS
- Suorien $L_1$ ja $L_2$ välinen kulma on tasan $90^\circ$.
Kaksi koordinaattiakselia määrää aina tason. Esimerkiksi $xy$-taso tarkoittaa $x$- ja $y$-akseleiden kautta kulkevaa tasoa, jossa kaikkien pisteiden $z$-koordinaatti on $0$. Suoran koordinaattimuotoisen parametriesityksen avulla voidaan löytää suoran ja tällaisen tason leikkauspiste. Tilannetta on havainnollistettu alla olevassa kuvassa.
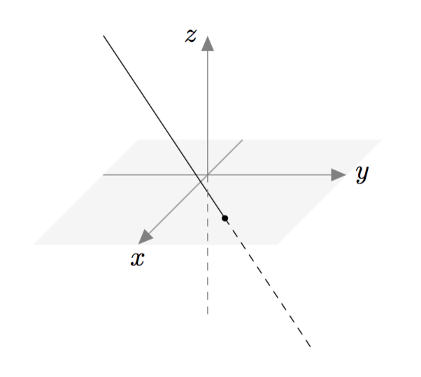
Suoran ja tason leikkauspiste
Suora $L_1$ kulkee pisteen $A = (1,1,2)$ kautta. Lisäksi tiedetään, että se on yhdensuuntainen suoran $L_2$ kanssa, jonka koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 15 + t \\ y &= -7 -2t \\ z &= -8 - t. \end{aligned}\right. $$ Tehtävänä on tutkia, missä pisteessä suora $L_1$ leikkaa $xz$-tason.
- Määritä suoralle $L_1$ suuntavektori.
- Muodosta suoran $L_1$ koordinaattimuotoinen parametriesitys.
- Mitkä seuraavista pisteistä ovat $xz$-tasossa? $B = (1,2,3)$, $C = (1,0,3)$, $D = (-5,0,9)$, $E = (1,2,0)$. Selitä omin sanoin.
- Pystyt päättelemään etsityn leikkauspisteen yhden koordinaatin arvon c-kohdan havaintoja hyödyntämällä. Valitse tätä koordinaattia vastaava yhtälö b-kohdan parametriesityksestä ja ratkaise siitä parametrin arvo.
- Mitkä ovat leikkauspisteen koordinaatit?
VASTAUS
- Suuntavektoriksi kelpaa esimerkiksi $\vi - 2\vj - \vk$.
- Yksi mahdollinen koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 1 + t \\ y &= 1 -2t \\ z &= 2 - t. \end{aligned}\right. $$
- Pisteet $C$ ja $D$.
- Etsitty leikkauspiste löydetään parametrin arvolla $t = \frac{1}{2}$.
- Leikkauspiste on $\left(\frac{3}{2}, 0, \frac{3}{2}\right)$
Alla olevassa mallikuvassa on havainnollistettu suoraa $L$, jonka vektorimuotoinen parametriesitys on $\pv{OP} = 2\vi + \vj + t(-2\vi + 3\vj + 2\vk)$. Tavoitteena on määrittää pisteen $Q = (-2,7,8)$ etäisyys suorasta $L$.
Etäisyyden määrittämiseksi on etsittävä suoran $L$ piste $P$, joka on lähimpänä pistettä $Q$. Se löydetään piirtämällä pisteen $Q$ kautta toinen suora, joka on kohtisuorassa suoraa $L$ vastaan.
Vektori $\pv{QP}$ voidaan kirjoittaa summana $$\pv{QP} = \pv{QA} + \pv{AP}.$$ Tässä vektori $\pv{QA}$ voidaan määrittää pisteiden $A = (2,1,0)$ ja $Q = (3,2,8)$ avulla. (Piste $A$ voidaan päätellä suoran $L$ parametriesityksestä.)
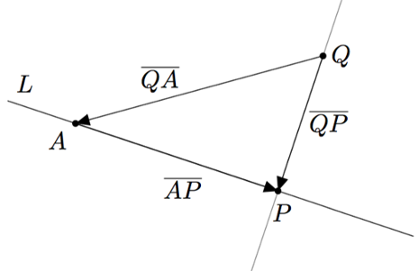
Vektoriksi $\pv{QA}$ saadaan $$\begin{align*} \pv{QA} &= (2-3)\vi + (1-2)\vj + (0-8)\vk \\ &= -\vi - \vj - 8\vk. \end{align*}$$ Vektori $\pv{AP}$ puolestaan on suoran $L$ suuntavektorin $\vv = -2\vi + 3\vj + 2\vk$ jokin skalaarimonikerta. (Suuntavektori voidaan lukea suoran $L$ parametriesityksestä.) Toisin sanottuna $$\begin{align*} \pv{AP} &= t\vv \\ &= t(-2\vi + 3\vj + 2\vk) \\ &= -2t\vi + 3t\vj + 2t\vk. \end{align*}$$ Vektoriksi $\pv{QP}$ saadaan siis $$\begin{align*} \pv{QP} &= \pv{QA} + \pv{AP} \\ &= (-\vi - \vj - 8\vk) + (-2t\vi + 3t\vj + 2t\vk) \\ &= (-1-2t)\vi + (-1+3t)\vj + (-8+2t)\vk. \end{align*}$$ Piste $P$ on lähimpänä pistettä $Q$, jos ja vain jos vektori $\pv{QP}$ on kohtisuorassa suoran $L$ suuntavektoria $\vv$ vastaan. Toisin sanottuna, jos ja vain jos $$\pv{QP} \cdot \vv = 0.$$ Kun tähän yhtälöön sijoitetaan edellä selvitetyt vektorit, se saadaan muotoon $$((-1-2t)\vi + (-1+3t)\vj + (-8+2t)\vk)\cdot (-2\vi + 3\vj + 2\vk) = 0.$$ Kun lasketaan pistetulo, yhtälö saadaan muotoon $$(-1-2t)\cdot (-2) + (-1+3t)\cdot 3 + (-8+2t)\cdot 2 = 0$$ ja sievennyksen sekä muutaman välivaiheen jälkeen muotoon $$17t -17 = 0.$$ Tästä saadaan ratkaistua $$t = 1.$$ Siten $$\begin{align*} \pv{QP} &= (-1-2t)\vi + (-1+3t)\vj + (-8+2t)\vk \\ &= -3\vi + 2\vj-6\vk. \end{align*}$$ Pisteen $Q$ etäisyys suorasta $L$ saadaan selville, kun lasketaan vektorin $\pv{QP}$ pituus $$\begin{align*} |\pv{QP}| &= \sqrt{(-3)^2 + 2^2 + (-6)^2}\\ &= \sqrt{49} = 7. \end{align*}$$
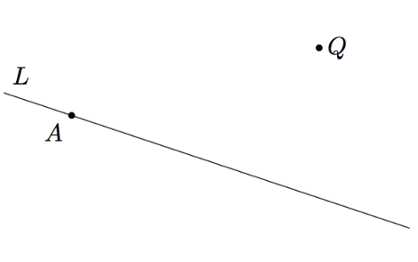
Pisteen etäisyys suorasta
Tehtävänä on määrittää alla olevan kuvan tilanteessa pisteen $Q = (4,4)$ etäisyys suorasta $L$.
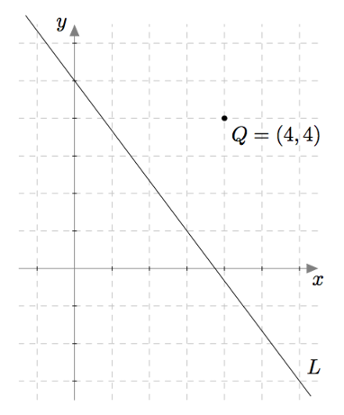
- Päättele kuvan avulla suoralle $L$ jokin suuntavektori $\vv$ ja jonkin suoran pisteen $A$ koordinaatit.
- Piirrä omaan vihkoosi koordinaatisto ja siihen suora $L$ sekä piste $Q$. Piirrä näkyviin myös se suoran $L$ piste, joka on lähinnä pistettä $Q$. Anna sille nimeksi $P$.
- Piirrä näkyviin vektorit $\pv{QA}$ ja $\pv{AP}$.
- Ilmaise vektori $\pv{QA}$ vektoreiden $\vi$ ja $\vj$ avulla. Ilmaise vektori $\pv{AP}$ suuntavektorin $\vv$ avulla. Tässä vaiheessa parametrin $t$ arvo on vielä tuntematon, mutta se ei haittaa.
- Ilmaise vektori $\pv{QP}$ vektoreiden $\pv{QA}$ ja $\pv{AP}$ avulla.
- Tutki pistetulon avulla, millä parametrin $t$ arvolla vektori $\pv{QP}$ on kohtisuorassa suoran $L$ suuntavektoria vastaan.
- Mikä on pisteen $Q$ etäisyys suorasta $L$?
- Mitkä ovat pisteen $P$ koordinaatit?
VASTAUS
- Etäisyys on $\frac{13}{5} = 2{,}6$.
- $P = \left(\frac{48}{25}, \frac{61}{25}\right) = (1{,}92; 2{,}44)$.
Taso
Tarkastellaan alla olevaa kuvaa. Pisteiden $A$, $B$ ja $C$ kautta on mahdollista piirtää ainoastaan yksi taso, sillä nämä pisteet eivät ole samalla suoralla.
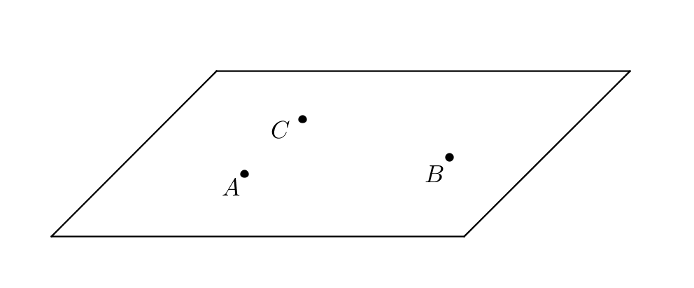
Kaksi pistettä tai kolme samalla suoralla olevaa pistettä ei riitä tason määräämiseen, sillä niiden kautta voi kulkea äärettömän monta eri tasoa.
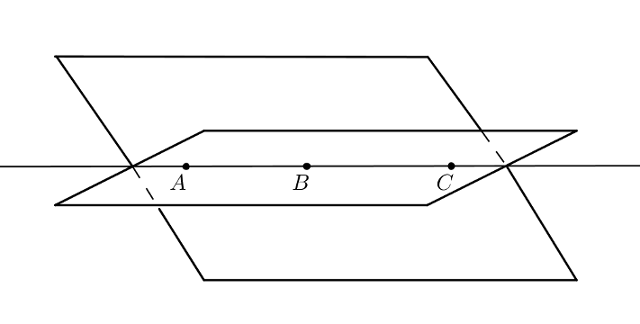
Vektoreiden avulla taso voidaan määrittää samaan tapaan kuin suora. Ainoa ero on, että tason määrittämiseen ei yksi suuntavektori riitä vaan niitä tarvitaan kaksi.
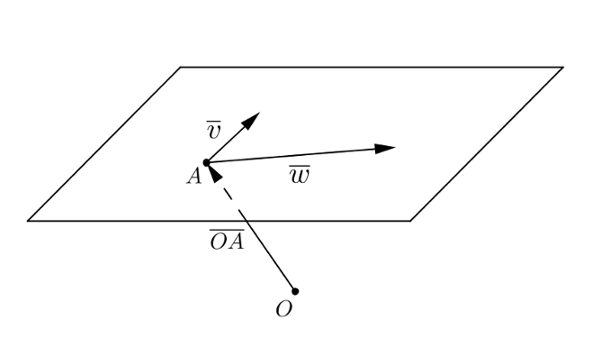
MÄÄRITELMÄ: TASON VEKTORIMUOTOINEN PARAMETRIESITYS
Oletetaan, että piste $A$ on tasossa $T$, jonka suuntavektorit ovat $\vv$ ja $\vw$. Oletetaan lisäksi, että $\vv \nparallel \vw$. Yhtälö $$\pv{OP} = \pv{OA} + s\vv + t\vw$$ on tason $T$ vektorimuotoinen parametriesitys.
Tässä esiintyvät kertoimet $s$ ja $t$ ovat parametreja ja vektori $\pv{OA}$ on tason paikkavektori.
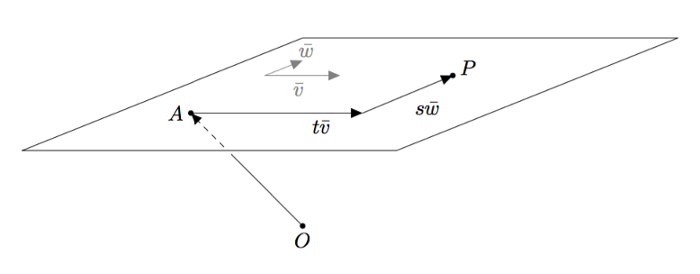
Tason vektorimuotoinen parametriesitys
Taso $T$ kulkee pisteiden $A = (-3,1,2)$, $B = (2,4,1)$ ja $C = (12,0,-1)$ kautta. Tarkan kuvan piirtäminen on hankalaa, mutta tilannetta voi kuitenkin havainnollistaa mallikuvalla:
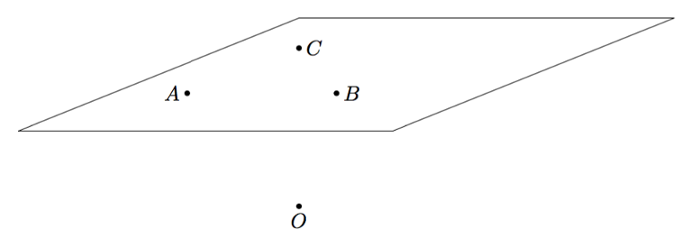
- Piirrä tilanteesta mallikuva omaan vihkoosi.
- Muodosta jonkin tason pisteen paikkavektori ja merkitse se mallikuvaan.
- Muodosta jotkin tason suuntaiset vektorit ja merkitse ne mallikuvaan.
- Tarkista, etteivät muodostamasi vektorit ole yhdensuuntaisia.
- Muodosta tason $T$ vektorimuotoinen parametriesitys.
- Määritä vektorimuotoisen parametriesityksen avulla kolme uutta pistettä tasosta $T$ antamalla eri arvoja parametreille $s$ ja $t$. Havainnollista näitä pisteitä mallikuvasi avulla.
Tason vektorimuotoinen parametriesitys kertoo, millaisia tason pisteiden paikkavektorit ovat. Kun siinä esiintyville parametreille $s$ ja $t$ annetaan eri arvoja, saadaan tason eri pisteiden paikkavektoreita samaan tapaan kuin suoran tilanteessa.
Tarkastellaan tasoa, jonka vektorimuotoinen parametriesitys on $$\pv{OP} = \vi + 2\vj + 3\vk + s(4\vi + 5\vk) + t(6\vi - 7\vj + 8\vk).$$ Sitä on havainnollistettu alla olevassa mallikuvassa:
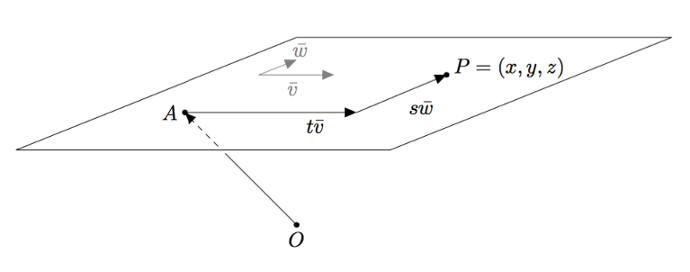
Jos pisteen $P$ koordinaatteja merkitään kirjaimilla $x$, $y$ ja $z$, voidaan yllä oleva parametriesitys kirjoittaa muodossa $$x\vi + y\vj + z\vk = \vi + 2\vj + 3\vk + s(4\vi + 5\vk) + t(6\vi - 7\vj + 8\vk).$$ Tämän yhtälön oikealla puolella voidaan kertoa sulut auki, jolloin yhtälö saadaan muotoon $$x\vi + y\vj + z\vk = \vi + 2\vj + 3\vk + 4s\vi + 5s\vk + 6t\vi - 7t\vj + 8t\vk.$$ Yhtälön oikeaa puolta voidaan vielä sieventää suorittamalla yhteenlaskut, minkä jälkeen yhtälö näyttää tältä: $$x\vi + y\vj + z\vk = (1+4s + 6t)\vi + (2-7t)\vj + (3+5s+8t)\vk.$$ Vektoreiden samuuden määritelmän mukaan tämä yhtälö toteutuu, jos ja vain jos yhtälön eri puolilla olevat vektorit voidaan ilmaista samalla tavalla vektoreiden $\vi$, $\vj$ ja $\vk$ avulla eli $$ \left\{\begin{aligned} x &= 1+4s + 6t \\ y &= 2-7t \\ z &= 3+5s+8t. \end{aligned}\right. $$ Minkä tahansa tason vektorimuotoinen parametriesitys voidaan muuttaa vastaavaan muotoon, jossa tason pisteen jokaiselle koordinaatille on oma yhtälönsä. Tätä esitystapaa sanotaan tason koordinaattimuotoiseksi parametriesitykseksi.
Tason koordinaattimuotoinen parametriesitys
Avaruuden taso $T$ kulkee pisteiden $A = (4,-1,3)$, $B = (2,1,3)$ ja $C = (7,-5,9)$ kautta.
- Piirrä tilanteesta mallikuva.
- Muodosta tason $T$ jonkin pisteen paikkavektori ja jotkin tason $T$ suuntavektorit. Varmista, etteivät suuntavektorit ole yhdensuuntaisia. Merkitse nämä mallikuvaan.
- Muodosta tason $T$ vektorimuotoinen parametriesitys.
- Muodosta tason $T$ koordinaattimuotoinen parametriesitys c-kohdan avulla.
- Määritä kaksi uutta tason $T$ pistettä antamalla parametreille eri arvoja.
Tason vektorimuotoisen parametriesityksen ja siitä saatavan koordinaattimuotoisen parametriesityksen avulla voidaan tutkia, onko jokin piste tasossa. Jos tarkastellun pisteen paikkavektoria ei saada tason parametriesityksestä millään parametrien $s$ ja $t$ arvoilla, voidaan päätellä, että tämä piste ei ole tasossa.
Onko piste tasossa?
Taso $T$ kulkee pisteiden $A = (-2,8,0)$, $B = (-2,12,-5)$ ja $C = (0,5,1)$ kautta.
- Muodosta tason $T$ vektorimuotoinen parametriesitys.
- Muodosta a-kohdan vektorimuotoisesta parametriesityksestä tason $T$ koordinaattimuotoinen parametriesitys.
- Muodosta b-kohdan koordinaattimuotoisesta parametriesityksestä yhtälöryhmä, jolla voit tutkia, onko piste $R = (6,-24,29)$ tasossa $T$. Ratkaise tämä yhtälöryhmä. Onko piste $R$ tasossa $T$? Jos on, millä parametrien arvoilla se saadaan parametriesityksestä?
- Onko piste $S = (2, -10,-13)$ tasossa $T$? Jos on, millä parametrien arvoilla se saadaan parametriesityksestä?
VASTAUS
- Piste $R$ on tasossa $T$.
- Piste $S$ ei ole tasossa $T$.
Tason koordinaattimuotoisesta parametriesityksestä voidaan tarvittaessa siirtyä takaisin vektorimuotoiseen parametriesitykseen samaan tapaan kuin suorien tapauksessa.
Tason vektorimuotoinen parametriesitys
Tehtävänä on muodostaa tason $T$ vektorimuotoinen parametriesitys, kun tiedetään, että sen koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 1+8s-2t \\ y &= 5+3s \\ z &= -7 -9s + 4t \end{aligned}\right. $$
- Määritä parametrien arvoja $s = 0$ ja $t = 0$ vastaava tason $T$ piste ja muodosta sen paikkavektori.
- Selitä, miten voit lukea a-kohdan paikkavektorin koordinaattimuotoisesta parametriesityksestä ilman laskuja.
- Miten voisit lukea tason kaksi suuntavektoria koordinaattimuotoisesta parametriesityksestä ilman laskuja?
- Olkoon $A$ parametrien arvoja $s = 0$ ja $t = 0$ vastaava tason piste, $B$ arvoja $s = 1$ ja $t = 0$ vastaava piste ja $C$ arvoja $s = 0$ ja $t = 1$ vastaava piste. Määritä nämä pisteet ja muodosta niiden avulla tason suuntavektorit $\pv{AB}$ ja $\pv{AC}$. Saitko saman tuloksen kuin c-kohdassa päättelemällä?
- Muodosta tason $T$ vektorimuotoinen parametriesitys.
VASTAUS
- Piste on $(1,5,-7)$ ja sen paikkavektori on $\vi + 5\vj - 7\vk$.
- $\pv{AB} = 8\vi + 3\vj - 9\vk\ $ ja $\ \pv{AC} = -2\vi + 4\vk$.
- Esimerkiksi $\pv{OP} = \vi + 5\vj - 7\vk + s(8\vi + 3\vj - 9\vk) + t(-2\vi + 4\vk)$.
Tutkitaan seuraavaksi suorien ja tasojen leikkauspisteitä. Suora ja taso leikkaavat toisensa, jos ja vain jos niillä on yhteinen piste. Toisin sanottuna suora ja taso leikkaavat toisensa, jos ja vain jos on olemassa piste $P$, jonka paikkavektori $\pv{OP}$ toteuttaa sekä suoran että tason parametriesityksen. Tätä on havainnollistettu alla olevassa kuvassa.
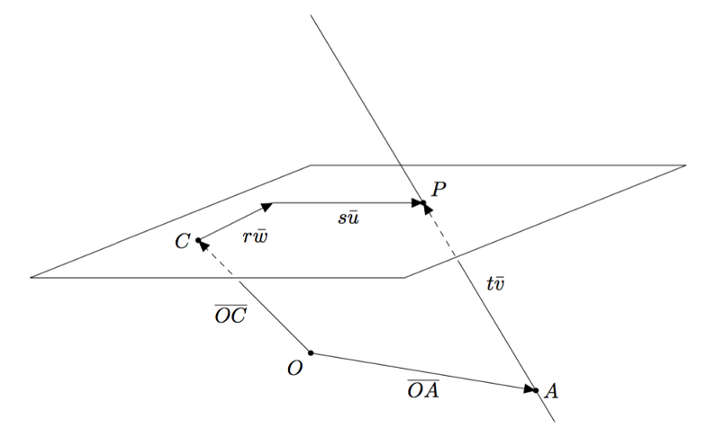
Jos suoran parametriesitys on $\pv{OP} = \pv{OA} + t\vv$ ja tason parametriesitys on $\pv{OP} = \pv{OC} + r\vw + s\vu$, löydetään suoran ja tason leikkauspiste tutkimalla yhtälöä $$\pv{OA} + t\vv = \pv{OC} + r\vw + s\vu.$$ Jos tällä yhtälöllä ei ole ratkaisua, tarkoittaa se, ettei tarkastelluilla suoralla ja tasolla ole yhtään leikkauspistettä.
Vektoriyhtälöstä $\pv{OA} + t\vv = \pv{OC} + r\vw + s\vu$ voidaan muodostaa yhtälöryhmä tarkastelemalla erikseen vektoreiden $\vi$, $\vj$ ja $\vk$ suuntaisia komponentteja. Esimerkiksi yhtälöä $$\vi-3\vj + t(\vi + \vj + \vk) = \vi + 2\vj + 3\vk + r(4\vi + 5\vk) + s(6\vi - 7\vj + 8\vk)$$ vastaa yhtälöryhmä $$ \left\{\begin{aligned} 1 + t &= 1+4r+6s &\quad &\text{(vektoreiden $\vi$ kertoimet)}\\ -3 + t &= 2 -7s &\quad &\text{(vektoreiden $\vj$ kertoimet)}\\ t &= 3 + 5r + 8s &\quad &\text{(vektoreiden $\vk$ kertoimet).} \end{aligned}\right. $$ Tämä yhtälöryhmä voidaan vielä muokata muotoon, jossa yhtälöiden kaikki tuntemattomat ovat yhtäsuuruusmerkin vasemmalla puolella ja vakiot oikealla puolella: $$ \left\{\begin{aligned} t -4r - 6s &= 0 \\ t + 7s&= 5 \\ t -5r -8s&= 3. \end{aligned}\right. $$ Tämän jälkeen yhtälöryhmä voidaan ratkaista tavalliseen tapaan kynän ja paperin avulla tai käyttämällä laskinta tai tietokonetta.
Suoran ja tason leikkauspiste
Suora $L$ kulkee pisteiden $A = (1,0,-2)$ ja $B = (2,1,1)$ kautta. Taso $T_1$ kulkee pisteen $C = (0,2,1)$ kautta. Lisäksi tiedetään, että se on yhdensuuntainen tason $T_2$ kanssa, jonka koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 11 + s \\ y &= -17 + t \\ z &= 28 - s + 2t. \end{aligned}\right. $$ Tehtävänä on tutkia, leikkaavatko suora $L$ ja taso $T_1$ toisensa, ja määrittää mahdollisen leikkauspisteen koordinaatit.
- Muodosta suoran $L$ vektorimuotoinen parametriesitys.
- Muodosta tason $T_1$ vektorimuotoinen parametriesitys. Käytä parametreina jotain muita kirjaimia kuin a-kohdassa.
- Jos suoralla $L$ ja tasolla $T_1$ on leikkauspiste, se toteuttaa sekä a- että b-kohdassa muodostamasi parametriesitykset joillakin parametrien arvoilla. Millaisen yhtälön saat tästä tiedosta?
- Muodosta c-kohdan yhtälöstä yhtälöryhmä tarkastelemalla erikseen vektoreiden $\vi$, $\vj$ ja $\vk$ suuntaisia komponentteja. Ratkaise tämä yhtälöryhmä.
- Leikkaavatko suora $L$ ja taso $T_1$ toisensa? Mitkä ovat mahdollisen leikkauspisteen koordinaatit?
VASTAUS
- Suora $L$ ja taso $T_1$ leikkaavat toisensa, leikkauspiste on $(0,-1,-5)$.
Koordinaattiakselin ja tason leikkauspiste
Taso $T$ kulkee pisteen $A = (1,1,2)$ kautta ja sillä on suuntavektorit $\vv = \vi-2\vj-\vk$ ja $\vw = 4\vi+7\vj-5\vk$. Tehtävänä on tutkia, missä pisteessä taso $T$ leikkaa $z$-akselin.
- Muodosta tason $T$ koordinaattimuotoinen parametriesitys.
- Mitkä seuraavista pisteistä ovat $z$-akselilla? $B = (1,2,0)$, $C = (1,0,3)$, $D = (0,0,9)$, $E = (1,0,0)$. Selitä omin sanoin.
- Pystyt päättelemään etsityn leikkauspisteen kahden koordinaatin arvon c-kohdan havaintoja hyödyntämällä. Valitse näitä koordinaatteja vastaavat yhtälöt b-kohdan parametriesityksestä ja ratkaise niistä parametrien arvot.
- Mitkä ovat leikkauspisteen koordinaatit?
VASTAUS
- Koordinaattimuotoinen parametriesitys on esimerkiksi $$ \left\{\begin{aligned} x &= 1 + s + 4t\\ y &= 1 - 2s + 7t \\ z &= 2 - s - 5t. \end{aligned}\right. $$
- Piste $D$.
- $s = -\frac{1}{5}$ ja $t = -\frac{1}{5}$.
- Leikkauspiste on $\left(0,0, \frac{16}{5}\right) = (0;0;3{,}2)$.
Pisteen etäisyys tasosta
Tarkastellaan tasoa $T$, jonka vektorimuotoinen parametriesitys on $\pv{OP} = -3\vi + 2\vj + \vk + s(\vi + 2\vj + 2\vk) + t(2\vi - 3\vk)$. Sitä on havainnollistettu alla olevassa mallikuvassa. Tehtävänä on määrittää kuvassa näkyvän pisteen $Q = (-28,31,-37)$ etäisyys tasosta $T$.
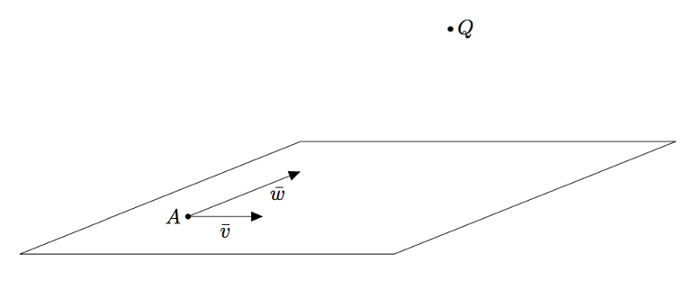
Etäisyyden määrittämiseksi on etsittävä tason $T$ piste $P$, joka on lähimpänä pistettä $Q$. Se löydetään piirtämällä pisteen $Q$ kautta suora, joka on kohtisuorassa tasoa $T$ vastaan. Tällaista suoraa sanotaan tason $T$ normaaliksi.
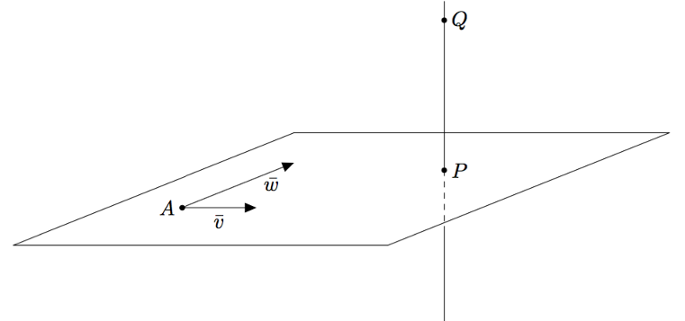
- Päättele tason parametriesityksestä, mitkä ovat tason suuntavektorit $\vw$ ja $\vv$. Päättele lisäksi tason pisteen $A$ koordinaatit.
- Piirrä omaan vihkoosi mallikuva tilanteesta. Merkitse kuvaan vektorit $\pv{QA}$ ja $\pv{AP}$.
- Ilmaise vektori $\pv{QA}$ vektoreiden $\vi$, $\vj$ ja $\vk$ avulla.
- Ilmaise vektori $\pv{AP}$ tason $T$ suuntavektoreiden $\vw$ ja $\vv$ avulla. Tässä vaiheessa parametrien $s$ ja $t$ arvot ovat tuntemattomia, mutta se ei haittaa. Ne ratkaistaan myöhemmin.
- Ilmaise vektori $\pv{QP}$ vektoreiden $\pv{QA}$ ja $\pv{AP}$ avulla.
- Vektorin $\pv{QP}$ pitää olla kohtisuorassa tason $T$ kumpaakin suuntavektoria vastaan. Mitä tämä tarkoittaa pistetulon kannalta? Muodosta kaksi yhtälöä.
- Muokkaa edellisessä kohdassa muodostamaasi kahta yhtälöä, kunnes pääset yhtälöpariin $$\left\{ \begin{aligned} 9s -4t &= -43 \\ -4s + 13 t &= 64. \end{aligned} \right.$$ Ratkaise tämä yhtälöpari.
- Kirjoita vektori $\pv{QP}$ vektoreiden $\vi$, $\vj$ ja $\vk$ avulla edellisen kohdan tuloksia hyödyntäen.
- Mikä on pisteen $Q$ etäisyys tasosta $T$?
- Mitkä ovat pisteen $P$ koordinaatit?
VASTAUS
- Suuntavektoreiksi voidaan valita $\vv = \vi + 2\vj + 2\vk$ ja $\vw = 2\vi - 3\vk$. Tason pisteeksi voidaan valita $A = (-3,2,1)$.
- $\pv{QA} = 25\vi - 29\vj + 38\vk$
- $\pv{AP} = s(\vi + 2\vj + 2\vk) + t(2\vi - 3\vk)$
- \begin{align*} \pv{QP} &= \pv{QA} + \pv{AP} \\ &= 25\vi - 29\vj + 38\vk \\ &{\phantom = {}} + s(\vi + 2\vj + 2\vk) \\ &{\phantom = {}} + t(2\vi - 3\vk) \end{align*}
- $\pv{QP} \cdot \vv = 0$ ja $\pv{QP} \cdot \vw = 0$.
- $s = -3$ ja $t = 4$
- $\pv{QP} = 30\vi - 35\vj + 20\vk$
- $\sqrt{2525} = 5\sqrt{101}$
- $P = (2, -4, -17)$
Normaalimuotoiset yhtälöt
Tarkastellaan alla olevan kuvan suoraa $L$, jonka vektorimuotoinen parametriesitys on $$\pv{OP} = 2\vi + \vj + t(2\vi - \vj).$$
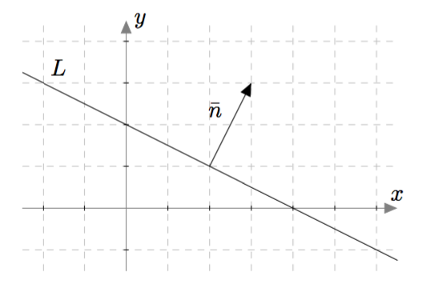
Kuvassa on näkyvissä vektori $\vn = \vi + 2\vj$, joka on kohtisuorassa suoran $L$ suuntavektoria $\vv = 2\vi - \vj$ vastaan. Tämä voidaan varmistaa laskemalla näiden vektoreiden pistetulo: $$\begin{align*} \vn \cdot \vv &= (\vi + 2\vj)\cdot (2\vi - \vj) \\ &= 1\cdot 2 + 2\cdot (-1) \\ &= 2-2 = 0. \end{align*} $$ Koska vektori $\vn$ on kohtisuorassa suoran $L$ suuntavektoria vastaan ja siten myös koko suoraa $L$ vastaan, sanotaan sitä suoran $L$ normaalivektoriksi.
Suoran normaalivektori
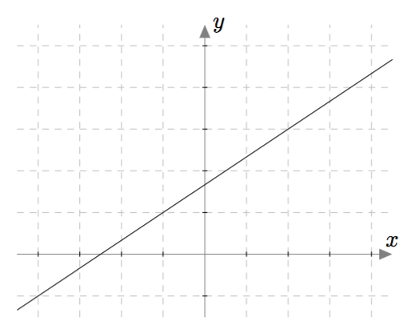
Keksi kaksi eri normaalivektoria alla olevan kuvan suoralle $L$. Tarkista pistetulon avulla, että löytämäsi vektorit ovat todella kohtisuorassa suoran $L$ suuntavektoria vastaan.
Suoran normaalivektori
Suoran $L$ vektorimuotoinen parametriesitys on $\pv{OP} = \vi - 2\vj + t(\vi + 4\vj)$.
- Mikä on tämän suoran paikkavektori? Entä suuntavektori?
- Piirrä suora $L$ koordinaatistoon.
- Etsi suoralle $L$ jokin normaalivektori $\vn$. Voit päätellä sen piirroksesta, mutta varmista pistetulon avulla, että se todella on kohtisuorassa suoran $L$ suuntavektoria vastaan.
VASTAUS
- Yksi paikkavektori on $\vi - 2\vj$. Yksi suuntavektori on $\vi + 4\vj$.
- Yksi normaalivektori on $4\vi-\vj$. Myös kaikki sen kanssa yhdensuuntaiset vektorit ovat suoran $L$ normaalivektoreita.
Tutkimalla alla olevaa kuvaa voidaan havaita, että piste $P = (x,y)$ on suoralla $L$, jos ja vain jos vektori $\pv{AP}$ on kohtisuorassa suoran normaalivektoria $\vn$ vastaan. Pistetulon avulla sama asia voidaan ilmaista sanomalla, että piste $P = (x,y)$ on suoralla $L$, jos ja vain jos $$\pv{AP} \cdot \vn = 0,$$ missä $\vn$ on suoran $L$ normaalivektori.
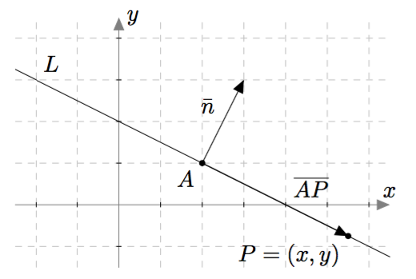
Kun yhtälöön $\pv{AP} \cdot \vn = 0$ sijoitetaan vektori $\pv{AP} = (x-2)\vi + (y-1)\vj$ ja suoran $L$ normaalivektori $\vn = \vi + 2\vj$, saadaan se muotoon $$((x-2)\vi + (y-1)\vj)\cdot (\vi + 2\vj)= 0.$$ Vasenta puolta voidaan sieventää laskemalla pistetulot: $$(x-2)\cdot 1 + (y-1)\cdot 2 = 0.$$ Sievennyksen jälkeen yhtälö saadaan muotoon $$x + 2y -4 = 0.$$
Suoran normaalivektori
Jatketaan äskeisen suoran $L$ tarkastelua. Edellä pääteltiin, että piste $P = (x,y)$ on tällä suoralla, jos ja vain jos se toteuttaa yhtälön $$x+2y-4 = 0.$$ Missä tässä yhtälössä näkyvät suoran $L$ normaalivektorissa $\vn = \vi + 2\vj$ esiintyvät kertoimet $1$ ja $2$?
MÄÄRITELMÄ: SUORAN NORMAALIMUOTOINEN YHTÄLÖ
Oletetaan, että $L$ on $xy$-tason suora ja $\vn = a\vi + b\vj$ on sen normaalivektori. Yhtälö $$ax + by + c = 0$$ on suoran $L$ normaalimuotoinen yhtälö.
Suoran normaalimuotoinen yhtälö
Tehtävänä on määrittää normaalimuotoinen yhtälö suoralle $L$, jonka vektorimuotoinen parametriesitys on $\pv{OP} = -\vi + 4\vj + t(\vi + 3\vj)$.
- Piirrä suora $L$ koordinaatistoon.
- Etsi suoralle $L$ jokin normaalivektori $\vn$. Voit päätellä sen piirroksesta, mutta varmista pistetulon avulla, että se todella on kohtisuorassa suoran $L$ suuntavektoria vastaan.
- Valitse piirroksestasi jokin suoran $L$ piste ja anna sille nimi $P$. Merkitse sen koordinaatteja $(x,y)$.
- Merkitse piirrokseesi vektori $\pv{AP}$. Tässä $A$ on suoran $L$ jokin piste, jonka koordinaatit tunnetaan.
- Ilmaise vektori $\pv{AP}$ vektoreiden $\vi$ ja $\vj$ avulla.
- Muodosta suoran $L$ normaalimuotoinen yhtälö muokkaamalla yhtälöä $$\pv{AP} \cdot \vn = 0$$ kunnes se on samassa muodossa kuin määritelmässä.
VASTAUS
- Yksi normaalivektori on $3\vi-\vj$. Myös kaikki sen kanssa yhdensuuntaiset vektorit ovat suoran $L$ normaalivektoreita.
- $3x - y + 7 = 0$
Suoran normaalimuotoinen yhtälö
Suoran $L$ normaalimuotoinen yhtälö on $2x + 3y - 2 = 0$.
- Piste $A$ on suoralla $L$ ja tiedetään, että sen $x$-koordinaatti on $4$. Selvitä suoran yhtälön avulla, mikä on pisteen $A$ $y$-koordinaatti.
- Etsi jokin toinen suoran $L$ piste antamalla sen $x$-koordinaatille jokin arvo ja laskemalla $y$-koordinaatin arvo suoran yhtälön avulla. Anna tälle pisteelle nimeksi $B$.
- Päättele suoran normaalimuotoisesta yhtälöstä suoran $L$ normaalivektori.
- Piirrä suora $L$ koordinaatistoon. Edellisten kohtien tiedoista on apua.
- Tarkista pistetulon avulla, että c-kohdassa päättelemäsi normaalivektori todella on kohtisuorassa suoran suuntavektoria $\pv{AB}$ vastaan.
- Määritä suora $L$ vektorimuotoinen parametriesitys.
VASTAUS
- $y = -2$
- Yksi suoran $L$ normaalivektori on $\vn = 2\vi + 3\vj$. Myös kaikki sen kanssa yhdensuuntaiset vektorit ovat suoran $L$ normaalivektoreita.
- Esimerkiksi $\pv{OP} = 4\vi - 2\vj + t(3\vi-2\vj)$.
Tarkastellaan tasoa $T$, jonka vektorimuotoinen parametriesitys on $$\pv{OP} = -3\vi + 2\vk + s(3\vi + \vk) + t(4\vi - \vj).$$ Sitä on havainnollistettu alla olevassa mallikuvassa.
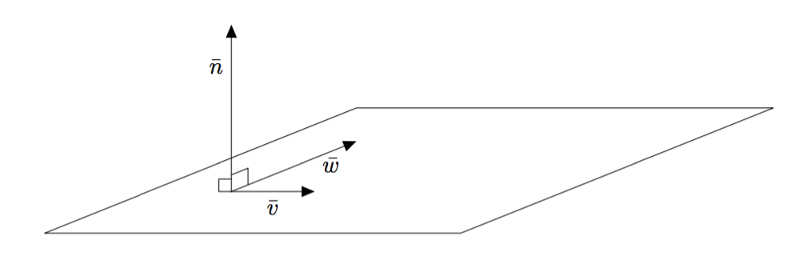
Kuvassa on näkyvissä vektori $\vn = \vi + 4\vj-3\vk$, joka on kohtisuorassa tason $%$ suuntavektoreita $\vw = 3\vi + \vk$ ja $\vv = 4\vi - \vj$ vastaan. Tämä voidaan varmistaa laskemalla näiden vektoreiden pistetulot: $$\begin{align*} \vn \cdot \vw &= (\vi + 4\vj-3\vk)\cdot (3\vi + \vk) \\ &= 1\cdot 3 + 4\cdot 0 + (-3)\cdot 1\\ &= 3-3 = 0. \end{align*} $$ ja $$\begin{align*} \vn \cdot \vv &= (\vi + 4\vj-3\vk)\cdot (4\vi - \vj) \\ &= 1\cdot 4 + 4\cdot (-1) + (-3)\cdot 0\\ &= 4-4 = 0. \end{align*} $$ Koska vektori $\vn$ on kohtisuorassa tason $T$ kumpaakin suuntavektoria vastaan ja siten myös koko tasoa $T$ vastaan, sanotaan sitä tason $T$ normaalivektoriksi.
Tason normaalivektori
Tason $T$ vektorimuotoinen parametriesitys on $\pv{OP} = 2\vi - 5\vj -2\vk + s(7\vi + 5\vk) + t(7\vj + 2\vk)$.
- Onko vektori $\vb = 3\vi-2\vj -2\vk$ tason $T$ normaalivektori?
- Onko vektori $\vc = 5\vi+2\vj -7\vk$ tason $T$ normaalivektori?
- Keksi tasolle $T$ vielä yksi normaalivektori. Mistä tiedät, että se todella on tason $T$ normaalivektori? Selitä omin sanoin.
VASTAUS
- Ei ole.
- On.
- Sopiva vektori on muotoa $t(5\vi+2\vj -7\vk)$, missä $t$ on mikä tahansa reaaliluku.
Tason normaalivektori
Tason $T$ vektorimuotoinen parametriesitys on $\pv{OP} = -\vi + 2\vk + s(\vi + 3\vj-2\vk) + t(2\vi + 2\vj-2\vk)$. Tehtävänä on etsiä tälle tasolle normaalivektori.
- Päättele parametriesityksestä, mitkä ovat tason $T$ suuntavektorit $\vw$ ja $\vv$.
- Merkitse etsittyä normaalivektoria $\vn = x\vi + y\vj + z\vk$. Sen täytyy olla kohtisuorassa tason $T$ kumpaakin suuntavektoria vastaan. Millaiset yhtälöt saat tästä pistetulon avulla?
- Edellisen kohdan yhtälöt johtavat yhtälöpariin $$ \left\{\begin{aligned} x+3y-2z &= 0\\ 2x+2y-2z &= 0. \end{aligned} \right. $$ Jos kumpaankin yhtälöön sijoitetaan tuntemattomien arvoiksi $x = 0$, $y = 0$ ja $z = 0$, yhtälöt toteutuvat. Yhtälöparilla on siis ainakin yksi ratkaisu $(x,y,z) = (0,0,0)$. Koska yhtälöparille löytyy yksi ratkaisu ja tuntemattomia on enemmän kuin yhtälöitä, on yhtälöparilla muitakin ratkaisuja. Niitä löydetään, kun yhdelle tuntemattomalle annetaan jokin nollasta poikkeava arvo ja ratkaistaan muiden tuntemattomien arvot sen jälkeen tavalliseen tapaan.
Koska tavoitteena on löytää yksi normaalivektori $\vn = x\vi + y\vj + z\vk$, riittää löytää yksi yllä olevan yhtälöparin nollasta poikkeava ratkaisu. Anna tuntemattomalle $z$ jokin nollasta poikkeava arvo ja ratkaise sen jälkeen yhtälöparista $x$ ja $y$. - Kirjoita vektori $\vn$ näkyviin vektoreiden $\vi$, $\vj$ ja $\vk$ avulla. Tarkista vielä pistetulon avulla, että se todella on kohtisuorassa vektoreita $\vw$ ja $\vv$ vastaan.
VASTAUS
- Voidaan valita esimerkiksi $\vw = \vi + 3\vj-2\vk$ ja $\vv = 2\vi + 2\vj-2\vk$.
- $\vv \cdot \vn = 0$ ja $\vw \cdot \vn = 0$
- Jos valitaan esimerkiksi $z = 2$, saadaan muiden tuntemattomien arvoiksi $x = 1$ ja $y = 1$.
- Yksi tason $T$ normaali on $\vn = \vi + \vj + 2\vk$. Myös kaikki sen kanssa yhdensuuntaiset vektorit ovat tason $T$ normaalivektoreita.
Tarkastellaan edelleen tasoa $T$, jonka vektorimuotoinen parametriesitys on $$\pv{OP} = -3\vi + 2\vk + s(3\vi + \vk) + t(4\vi - \vj).$$ Tutkimalla alla olevaa kuvaa voidaan havaita, että piste $P = (x,y,z)$ on tasossa $T$, jos ja vain jos vektori $\pv{AP}$ on kohtisuorassa tason normaalivektoria $\vn = \vi + 4\vj-3\vk$ vastaan. Pistetulon avulla sama asia voidaan ilmaista sanomalla, että piste $P = (x,y,z)$ on tasossa $T$, jos ja vain jos $$\pv{AP} \cdot \vn = 0,$$ missä $\vn$ on tason $T$ normaalivektori.
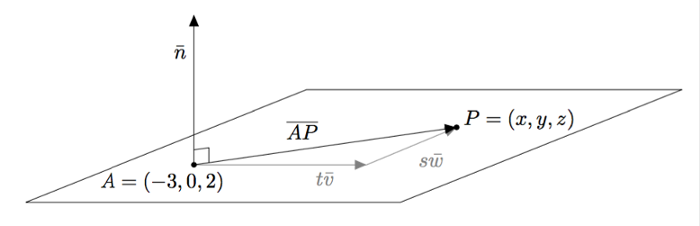
Kun yhtälöön $\pv{AP} \cdot \vn = 0$ sijoitetaan vektori $\pv{AP} = (x+3)\vi + (y-0)\vj + (z-2)\vk$ ja tason $T$ normaalivektori $\vn = \vi + 4\vj-3\vk$, saadaan se muotoon $$((x+3)\vi + y\vj + (z-2)\vk)\cdot (\vi + 4\vj-3\vk)= 0.$$ Vasenta puolta voidaan sieventää laskemalla pistetulot: $$(x+3)\cdot 1 + 4y + (z-2)\cdot (-3) = 0.$$ Sievennyksen jälkeen yhtälö saadaan muotoon $$x + 4y -3z +9 = 0.$$
Tason normaalivektori
Jatketaan äskeisen tason $T$ tarkastelua. Edellä pääteltiin, että piste $P = (x,y,z)$ on tässä tasossa, jos ja vain jos se toteuttaa yhtälön $$x + 4y -3z +9 = 0.$$ Missä tässä yhtälössä näkyvät tason $T$ normaalivektorissa $\vn = \vi + 4\vj-3\vk$ esiintyvät kertoimet $1$, $4$ ja $-3$?
MÄÄRITELMÄ: TASON NORMAALIMUOTOINEN YHTÄLÖ
Oletetaan, että $\vn = a\vi + b\vj + c\vk$ on tason $T$ normaalivektori. Yhtälö $$ax + by + cz + d = 0$$ on tason $T$ normaalimuotoinen yhtälö.
Tason normaalimuotoinen yhtälö
Tehtävänä on määrittää normaalimuotoinen yhtälö tasolle $T$, jonka vektorimuotoinen parametriesitys on $\pv{OP} = -\vi + 2\vk + s(\vi + 3\vj-2\vk) + t(2\vi + 2\vj-2\vk)$.
- Piirrä tilanteesta mallikuva.
- Päättele tason $T$ parametriesityksestä tason jonkin pisteen koordinaatit. Anna tälle pisteelle nimi $A$.
- Valitse piirroksestasi jokin tason $T$ piste ja anna sille nimi $P$. Merkitse sen koordinaatteja $(x,y,z)$.
- Merkitse piirrokseesi vektori $\pv{AP}$.
- Ilmaise vektori $\pv{AP}$ vektoreiden $\vi$, $\vj$ ja $\vk$ avulla.
- Tehtävässä 30 etsittiin tasolle $T$ normaalivektori $\vn$. Muodosta tason $T$ normaalimuotoinen yhtälö muokkaamalla yhtälöä $$\pv{AP} \cdot \vn = 0$$ kunnes se on samassa muodossa kuin määritelmässä.
- Muodosta tason $T$ normaalimuotoinen yhtälö laskimen tai tietokoneen avulla ja tarkista edellisessä kohdassa saamasi vastaus. Katso tarvittaessa mallia TI-Nspiren käyttöön tästä videosta.
VASTAUS
- Esimerkiksi $A = (-1,0,2)$.
- $\pv{AP} = (x+1)\vi + y\vj + (z-2)\vk$
- $x + y + 2z - 3 = 0$
Tason normaalimuotoinen yhtälö
Tason $T$ normaalimuotoinen yhtälö on $-x + 3y + 2z - 5= 0$.
- Piste $A$ on tasossa $T$ ja tiedetään, että $A = (4,5,z)$. Selvitä tason yhtälön avulla, mikä on pisteen $A$ $z$-koordinaatti.
- Etsi jokin toinen tason $T$ piste antamalla sen $x$- ja $y$-koordinaateille jotkin arvot ja laskemalla $z$-koordinaatin arvo tason yhtälön avulla. Anna tälle pisteelle nimeksi $B$.
- Muodosta tasolle $T$ yksi suuntavektori pisteiden $A$ ja $B$ avulla. Piirrä tilanteesta mallikuva.
- Päättele tason normaalimuotoisesta yhtälöstä tason $T$ normaalivektori. Anna sille nimeksi $\vn$.
- Keksi jokin vektori $\vv \nparallel \pv{AB}$, joka on kohtisuorassa vektoria $\vn$ vastaan. Tarkista kohtisuoruus pistetulon avulla. Jos haluat, voit etsiä vektorin $\vv$ samaan tapaan kuin kohdissa (b)-(c).
- Määritä tason $T$ vektorimuotoinen parametriesitys a-, c- ja e-kohtien avulla.
VASTAUS
- $z = -3$
- $\vn = -\vi + 3\vj + 2\vk$
- Esimerkiksi $2\vi + \vk$ tai $3\vi + \vj$.
Tason normaalivektoria voidaan hyödyntää myös suoran ja tason välisen kulman määrittämiseen. Alla oleva mallikuva havainnollistaa edellisen tehtävän tasoa $T$, jonka normaalimuotoinen yhtälö on $-x + 3y + 2z - 5= 0$. Kuvassa on lisäksi suora $L$, jolla on parametriesitys $\pv{OP} = 2\vi + \vk + t(-\vi + \vj + 2\vk)$.
Tason $T$ yhtälöstä voidaan päätellä, että tasolla $T$ on normaali $\vn = -\vi + 3\vj + 2\vk$. Suoran $L$ parametriesityksestä voidaan päätellä, että suoralla $L$ on suuntavektori $\vv = -\vi + \vj + 2\vk$. Näiden välinen kulma voidaan laskea pistetulon avulla: $$\begin{align*} \cos(\vn, \vv) &= \frac{\vn\cdot\vv}{|\vn||\vv|} \\ &= \frac{(-1)\cdot(-1) + 3\cdot 1 + 2\cdot 2}{\sqrt{(-1)^2 + 3^2 + 2^2}\sqrt{(-1)^2 + 1^2 + 2^2}} \\ &= \frac{8}{\sqrt{14}\sqrt{6}} \ (\approx 0{,}87287156). \end{align*}$$ Laskimella saadaan tästä $\sphericalangle(\vn,\vv) = 29{,}205932\ldots \approx 29{,}2^\circ$. Tämä on siis suoran $L$ ja tason normaalin välinen kulma. Koska tason normaalin ja tason välinen kulma on $90^\circ$, saadaan suoran ja tason välinen kulma $\alpha$ vähennyslaskulla: $$\alpha = 90^\circ - 29{,}2^\circ = 60{,}8^\circ.$$ Suoran $L$ ja tason $T$ välinen kulma on siis noin $60{,}8^\circ$.
Suoran ja tason välinen kulma
Suoran $L$ koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x &= 15 + t \\ y &= -7 -2t \\ z &= -8 - t. \end{aligned}\right. $$ Tehtävänä on määrittää suoran $L$ ja $xy$-tason välinen kulma.
- Piirrä $xyz$-koodinaatisto. Mitkä seuraavista pisteistä ovat $xy$-tasossa? $B = (3,4,0)$, $C = (0,3,4)$, $D = (3,0,0)$, $E = (0,4,0)$, $F = (0,0,3)$.
- Keksi $xy$-tasolle jokin normaalivektori $\vn$. Mistä tiedät, että se on $xy$-tason normaalivektori? Selitä omin sanoin.
- Päättele suoran $L$ parametriesityksestä suoran $L$ suuntavektori $\vv$.
- Laske vektorien $\vn$ ja $\vv$ välinen kulma. Mikä on suoran $L$ ja $xy$-tason välinen kulma? Anna vastaus asteen kymmenesosan tarkkuudella.
VASTAUS
- Pisteet $B$, $D$ ja $E$.
- Esimerkiksi $\vk$.
- Voidaan valita $\vv = \vi - 2\vj - \vk$.
- $\sphericalangle(\vv, \vn) \approx 114{,}1^\circ$, joten suoran $L$ ja $xy$-tason välinen kulma on noin $24{,}1^\circ$.
TEHTÄVÄSARJA II
Suora
Suora $L$ kulkee pisteen $A=(-2,3)$ kautta ja sen eräs suuntavektori on $\vv=4\vi-3\vj$.
- Piirrä tilanteesta kuva koordinaatistoon.
- Muodosta suoran $L$ vektorimuotoinen parametriesitys.
- Tutki parametriesityksen avulla, onko piste $B=(1,2)$ suoralla $L$. Tarkista tuloksesi kuvan avulla.
VASTAUS
- Esimerkiksi $\pv{OP} = -2\vi + 3\vj + t(4\vi-3\vj)$.
- Piste $B$ ei ole suoralla $L$.
Suora
Suoran $L$ koordinaattimuotoinen parametriesitys on $$ \left\{\begin{aligned} x&=2+3t\\ y&=-t\\ z&=1+t. \end{aligned} \right. $$
- Määritä suoralta $L$ kolme pistettä.
- Tutki, onko piste $(-10,4,-3)$ suoralla $L$.
- Määritä suoran $L$ jokin suuntavektori.
- Muodosta suoran $L$ vektorimuotoinen parametriesitys.
VASTAUS
- Esimerkiksi $(2,0,1)$, $(5,-1,2)$ ja $(8,-2,3)$.
- Kyllä, tämä piste on suoralla $L$.
- Esimerkiksi $3\vi - \vj + \vk$.
- Esimerkiksi $\pv{OP} = 2\vi + \vk + t(3\vi - \vj + \vk)$.
Suora
Tehtävänä on tutkia, ovatko kolme annettua pistettä samalla suoralla.
- Selitä omin sanoin, mitä tiedät tilanteesta, jossa kolme pistettä ovat samalla suoralla. Miten esimerkiksi vektoreiden yhdensuuntaisuus ja suoran vektorimuotoinen parametriesitys liittyvät asiaan? Keksitkö muita käsitteitä, jotka liittyvät tällaiseen tehtävään?
- Selitä omin sanoin, mitä tiedät tilanteesta, jossa kolme pistettä eivät ole samalla suoralla.
- Käytä edellisten kohtien pohdintojasi apuna ja tutki, ovatko pisteet $(-2,1), (3,2)$ ja $(4,3)$ samalla suoralla. Koska pisteet ovat $xy$-koordinaatistossa, piirrä tilanteen hahmottamiseksi pisteet koordinaatistoon.
VASTAUS
- Pisteet eivät ole samalla suoralla.
Suorien leikkauspiste
Suora $L_1$ kulkee pisteiden $A=(1,2,3)$ ja $B=(-1,0,3)$ kautta. Suora $L_2$ kulkee pisteiden $C=(-2,1,0)$ ja $D=(0,2,1)$ kautta.
- Muodosta kummallekin suoralle vektorimuotoinen parametriesitys.
- Muodosta parametriesityksistä yhtälö ja tutki, leikkaavatko suorat $L_1$ ja $L_2$. Myönteisessä tapauksessa määritä leikkauspisteen koordinaatit.
VASTAUS
- Suoran $L_1$ parametriesitykseksi voidaan valita esimerkiksi $\pv{OP} = \vi + 2\vj + 3\vk + t(-2\vi-2\vj)$ ja suoran $L_2$ parametriesitykseksi $\pv{OP} = -2\vi + \vj + s(2\vi + \vj + \vk)$
- Suorat eivät leikkaa.
Suorien välinen kulma
Suora $L_1$ kulkee pisteiden $(3,4)$ ja $(6,-2)$ kautta. Suoran $L_2$ koordinaattimuotoinen parametriesitys on $$ \left\{ \begin{aligned} x&=-2+3t\\ y&=1-t. \end{aligned} \right. $$
- Piirrä suorat sekä suorien välinen kulma koordinaatistoon.
- Määritä suorien välinen kulma asteen kymmenesosan tarkkuudella.
- Tarkista vastauksesi järkevyys mittaamalla kulman suuruus piirroksestasi.
VASTAUS
- Kulma on tasan $45^\circ$.
Suorien leikkauspiste
Suora $L_1$ kulkee pisteen $(1,-1,2)$ kautta ja sen eräs suuntavektori on $\vv=-2\vi+\vj+3\vk$. Suora $L_2$ kulkee pisteen $(3,5,-1)$ kautta ja se leikkaa suoran $L_1$ kohtisuorasti. Määritä leikkauspisteen koordinaatit.
VASTAUS
Leikkauspiste on $\left(2, -\frac{3}{2}, \frac{1}{2}\right)$.
Suoran normaalimuotoinen yhtälö
Suoran $L$ normaalimuotoinen yhtälö on $3x-y+5=0$.
- Määritä suoran $L$ jokin normaalivektori.
- Päättele suoran $L$ jokin suuntavektori joko yhtälöstä tai kuvasta. Tarkista päättelysi pistetulon avulla.
- Määritä suoralta jokin piste.
- Muodosta suoran koordinaattimuotoinen parametriesitys.
VASTAUS
- Esimerkiksi $3\vi - \vj$.
- Esimerkiksi $\vi + 3\vj$.
- Esimerkiksi $(1,8)$.
- Koordinaattimuotoinen parametriesitys on esimerkiksi $$ \left\{ \begin{aligned} x&=1+t\\ y&=8+3t. \end{aligned} \right. $$
Suoran ja $xz$-tason välinen kulma
Tarkastele suoraa $L$, joka kulkee pisteiden $(-1,1,3)$ ja $(5,-3,4)$ kautta.
- Mitä tiedät $xz$-tason pisteiden koordinaateista? Käytä tätä tietoa sekä sopivaa parametriesitystä ja määritä suoran $L$ ja $xz$-tason leikkauspiste.
- Keksi $xz$-tasolle jokin normaalivektori.
- Määritä suoran $L$ ja $xz$-tason välinen kulma asteen tarkkuudella.
VASTAUS
- Leikkauspiste on $\left(\frac{1}{2},0, \frac{13}{4}\right) = (0{,}5; 0; 3{,}25)$.
- Esimerkiksi $\vj$.
- Kulma on noin $33^\circ$.
Pisteen etäisyys suorasta
Suoran $L$ vektorimuotoinen parametriesitys on $\pv{OP}=\vi-2\vj+t(-2\vi+3\vj)$. Määritä pisteen $(3,4)$ etäisyys suorasta $L$. Koska tehtävä on $xy$-tasossa, piirrä kuva koordinaatistoon ja tarkista vastauksesi järkevyys sen avulla.
VASTAUS
Etäisyys on $\dfrac{6}{13}\sqrt{117} \approx 4{,}99$.
Pisteen etäisyys suorasta
Laske pisteen $Q = (3,-1,0)$ etäisyys pisteiden $A = (-3,-2,1)$ ja $B = (5,4,-3)$ kautta kulkevasta suorasta.
VASTAUS
Etäisyys on tasan 3.
Taso
Taso $T$ kulkee pisteiden $(1,0,3)$, $(-2,1,2)$ ja $(3,4,1)$ kautta.
- Nimeä pisteet ja muodosta tasolle suuntavektorit.
- Muodosta tasolle vektorimuotoinen parametriesitys.
- Muodosta tasolle koordinaattimuotoinen parametriesitys.
- Tutki, onko piste $(5,3,0)$ tasossa $T$.
VASTAUS
- Esimerkiksi $A = (1,0,3)$, $B = (-2,1,2)$ ja $C = (3,4,1)$. Suuntavektoreiksi voi valita esimerkiksi $\pv{AB} = -3\vi + \vj - \vk$ ja $\pv{AC} = 2\vi + 4\vj - 2\vk$, sillä nämä vektorit eivät ole yhdensuuntaiset.
- Esimerkiksi $\pv{OP} = \vi + 3\vk + s(-3\vi + \vj - \vk) + t(2\vi + 4\vj - 2\vk)$.
- Koordinaattimuotoinen parametriesitys on esimerkiksi $$ \left\{ \begin{aligned} x&=1-3s+2t\\ y&=s+4t\\ z&=3-s-2t. \end{aligned} \right. $$
- Piste $(5,3,0)$ ei ole tasossa $T$.
Suoran ja tason leikkauspiste
Tason $T$ eräät suuntavektorit ovat $\vv=\vi+2\vk$ ja $\vw=3\vi+\vj-\vk$. Lisäksi piste $(1,0,0)$ on tasossa. Suoran $L$ koordinaattimuotoinen parametriesitys on $$ \left\{ \begin{aligned} x&=1+3t\\ y&=-t\\ z&=5+2t. \end{aligned} \right. $$ Piirrä tilanteesta mallikuva. Tutki parametriesitysten avulla, leikkaavatko suora $L$ ja taso $T$. Määritä mahdollisen leikkauspisteen koordinaatit.
VASTAUS
Leikkauspiste on $\dfrac{1}{11}(26,-5,65)$.
Suoran normaalimuotoinen yhtälö
Suora $L$ kulkee pisteiden $A = (2,1)$ ja $B = (3,5)$ kautta.
- Piirrä suora $L$ koordinaatistoon.
- Määritä suoralle $L$ suuntavektori.
- Keksi tai etsi suoralle $L$ normaalivektori. Tarkista kohtisuoruus pistetulon avulla.
- Muodosta suoran $L$ normaalimuotoinen yhtälö.
VASTAUS
- Esimerkiksi $\vi + 4\vj$.
- Esimerkiksi $4\vi - \vj$.
- $4x - y - 7 = 0$.
Tason normaalimuotoinen yhtälö
Taso $T$ kulkee pisteiden $A = (1,-3,0)$, $B = (4,0,3)$ ja $C = (5,2,2)$ kautta.
- Perustele, että vektori $\vn = 3\vi - 2\vj - \vk$ on tason $T$ normaalivektori.
- Muodosta tasolle $T$ normaalimuotoinen yhtälö.
VASTAUS
- Tason $T$ suuntavektoreiksi voidaan valita esimerkiksi $\pv{AB}$ ja $\pv{AC}$. Kun lasketaan pistetulot $\pv{AB} \cdot \vn$ ja $\pv{AC} \cdot \vn$, huomataan, että vektori $\vn$ on kohtisuorassa tason $T$ kumpaakin suuntavektoria vastaan. Se on siten tason $T$ normaalivektori.
- $3x-2y-z-9 = 0$
Pisteen etäisyys tasosta
Taso $T$ kulkee origon sekä pisteiden $(0,2,1)$ ja $(3,-2,-2)$ kautta. Laske pisteen $(1,-3,4)$ etäisyys tasosta $T$.
VASTAUS
Etäisyys on tasan 1.
TEHTÄVÄSARJA III
Osoita, että pisteet $A = (-3,6,4)$, $B = (2,-4,-1)$ ja $C = (-1,2,2)$ ovat samalla suoralla. Missä suhteessa piste $C$ jakaa janan $AB$?
VASTAUS
$\pv{AC} = 2\vi - 4\vj - 2\vk$ ja $\pv{AB} = 5\vi - 10\vj - 5\vk$. Vektorit $\pv{AC}$ ja $\pv{AB}$ ovat yhdensuuntaiset, sillä $\pv{AC} = \frac{2}{5}\pv{AB}$. Tästä voidaan myös päätellä, että piste $C$ jakaa janan $AB$ suhteessa $2:3$.
Lasersäteellä osoitetaan pisteestä $A(1,-2,3)$ vektorin $\vu=2\vi-\vj-3\vk$ suuntaan. Toisella säteellä osoitetaan pisteestä $B(9,-1,-12)$ vektorin $\vv=-\vi-2\vj+3\vk$ suuntaan. Näytä, että säteet leikkaavat toisensa, ja määritä niiden leikkauspiste. [Pitkä K2014/8]
VASTAUS
Kysytty leikkauspiste on $(7, -5, -6)$.
Ovatko pisteet $A = (-3,2,1)$, $B = (-2,4,3)$, $C = (-1,2,-2)$ ja $D = (2,8,3)$ samassa tasossa?
VASTAUS
Pisteiden $A$, $B$ ja $C$ kautta kulkevan tason yksi parametriesitys on $\pv{OP} = -3\vi + 2\vj + \vk + s(\vi + 2\vj + 2\vk) + t(2\vi-3\vk)$. Kun tutkitaan, saadaanko tästä piste $D$ joillakin parametrien $s$ ja $t$ arvoilla, huomataan, että piste $D$ ei ole samassa tasossa muiden pisteiden kanssa.
Pisteiden $A(2,0,1)$ ja $B(3,1,3)$ yhdysjanan keskipisteen kautta asetetaan taso, joka on kohtisuorassa yhdysjanaa vastaan. Missä pisteessä tämä taso leikkaa $y$-akselin?
[Pitkä K2013/7]
VASTAUS
Leikkauspiste on $(0,7,0)$.
Suora $L$ kulkee pisteiden $(8,-3,7)$ ja $(2,5,-1)$ kautta.
- Missä pisteessä suora $L$ leikkaa $xy$-tason?
- Kuinka suuri on suoran $L$ ja $xy$-tason välinen kulma?
VASTAUS
- Pisteessä $\left(\frac{11}{4}, 4, 0\right) = (2{,}75; 4; 0)$.
- Noin $38{,}7^\circ$.
Laske pisteiden $(-2,4,-5)$ ja $(4,-2,2)$ kautta kulkevan suoran ja koordinaattiakselien väliset kulmat.
VASTAUS
Suoran ja $x$-akselin välinen kulma noin $56{,}9^\circ$, samoin suoran ja $y$-akselin välinen kulma. Suoran ja $z$-akselin välinen kulma noin $50{,}5^\circ$.
Suora $L$ kulkee pisteiden $A = (1,1,-2)$ ja $B = (5,-5,6)$ kautta. Laske pisteen $Q = (2,4,7)$ etäisyys suorasta $L$. Mikä suoran $L$ piste on lähinnä pistettä $Q$?
VASTAUS
Lähin piste on $(3, -2, 2)$ ja kysytty etäisyys on $\sqrt{62}$.
Pisteiden $A = (2,0,0)$, $B = (0,3,0)$ ja $C = (0,0,4)$ kautta kulkevalle tasolle $T$ asetetaan normaali (eli tasoa vastaan kohtisuorassa oleva suora) pisteeseen $C$. Missä pisteessä normaali leikkaa $xy$-tason?
VASTAUS
Pisteessä $\left(-8, -\frac{16}{3}, 0\right)$.
Suorakulmaisen kolmion kaksi kärkeä ovat origo ja $A = (1,3,0)$. Sen kolmas kärki $B$ on origon ja pisteen $C = (0,1,1)$ kautta kulkevalla suoralla. Määritä pisteen $B$ koordinaatit.
VASTAUS
$B = \left(0, \frac{3}{2}, \frac{3}{2}\right)$ tai $B = \left(0, \frac{10}{3}, \frac{10}{3}\right)$
Missä pisteessä origon ja pisteen $(1,2,3)$ kautta kulkeva suora $L$ leikkaa pisteiden $(1,0,0)$, $(0,1,0)$ ja $(0,0,1)$ kautta kulkevan tason $T$? Kuinka suuri on suoran $L$ ja tason $T$ välinen kulma?
VASTAUS
Leikkauspiste on $\frac{1}{6}(1,2,3)$. Kulma on noin $67{,}8^\circ$.
Määritä normaalimuotoinen yhtälö suoralle, joka kulkee pisteen $(2,-3)$ kautta ja on
- $x$-akselin suuntainen
- $y$-akselin suuntainen
- suoran $2x+3y-4 = 0$ suuntainen.
VASTAUS
- $y + 3 = 0$
- $x - 2 = 0$
- $2x + 3y + 5 = 0$.
Avomerellä suoran rannikon edustalla ajelehtiva vene havaittiin ensimmäisen kerran 15,2 km laiturista $L$ etelään. Myöhemmin se nähtiin ajelehtimassa 8,6 km laiturista $M$ etelään. Laituri $M$ sijaitsee 11,4 km itään laiturista $L$. Missä kohdassa vene ajautuu maihin, jos tuulen suunta pysyy samana?
VASTAUS
Noin 26,3 km laiturista $L$ itään (eli noin 14,9 km laiturista $M$ itään).
Lintujen kevätmuuttoa tarkkailtiin kukkulalta $K$. Sieltä 400 m etelään on piste $A$, josta puolestaan 400 m länteen on piste $B$. Piste $C$ on 500 m itään kukkulasta $K$ ja piste $D$ on 200 m pohjoiseen pisteestä $C$. Kuikka lensi suoraviivaista reittiä pisteiden $B$ ja $K$ yli, kaakkuri puolestaan lensi suoraviivaista reittiä pisteiden $A$ ja $D$ yli. Havaitsija $H$ kertoi nähneensä molemmat linnut suoraan yläpuolellaan. Missä paikassa $H$ teki havaintonsa?
VASTAUS
Havaitsija $H$ teki havaintonsa pisteessä, joka sijaitsee kukkulasta 2 km itään ja 2 km pohjoiseen.
Määritä suoran $2x-y+4 = 0$ se piste, joka on yhtä etäällä pisteistä $(0,-3)$ ja $(4,-1)$.
VASTAUS
Kysytty piste on $\left(-\frac{1}{2}, 3\right) = (-0{,}5; 3)$.
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

