Geometriaa vektoreiden avulla
Luvun tavoitteet
Tämän luvun tavoitteena on, että osaat käyttää vektoreita geometristen ongelmien ratkaisemiseen ilman koordinaatistoa. Lisäksi vahvistat edellisissä luvuissa harjoiteltuja taitoja:
- vektorien laskutoimitusten tulkitsemista geometrisesti (yhteen- ja vähennyslasku sekä reaaliluvulla kertominen)
- pistetulon laskusääntöjen ja ominaisuuksien soveltamista geometristen ongelmien ratkaisemiseen.
Geometriaa vektoreiden avulla
Edellisissä luvuissa olemme tutustuneet $xy$- ja $xyz$-koordinaatistojen vektoreihin ja niillä laskemiseen. Vektoreita voidaan kuitenkin käyttää myös ilman koordinaatistoa. Mallikuvat, joita olemme piirtäneet kolmiulotteisen avaruuden tilanteista, ovat olleet askel tähän suuntaan.
Palautetaan mieleen, että vektoreiden summan $\bar{v}+\bar{w}$ voi määrittää piirtämällä vektorit $\bar{v}$ ja $\bar{w}$ peräkkäin. Erotuksen $\bar{v}-\bar{w}$ voi puolestaan määrittää piirtämällä peräkkäin vektorit $\bar{v}$ ja $-\bar{w}$. Esimerkiksi alla olevassa kuvassa $$\begin{align*} \va &= \vb + \vc \\ \vb &= \va - \vc \\ \vc &= -\vb + \va = \va - \vb. \end{align*}$$
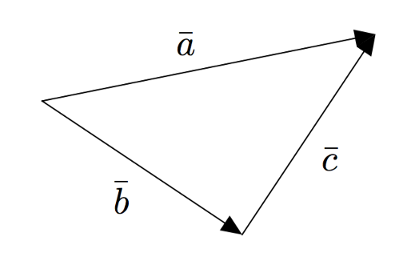
Vektoreiden yhteen- ja vähennyslasku
Alla on kuvattu suunnikas $ABCD$. Ilmaise sen sivuvektoreiden $\va$ ja $\vb$ avulla
- lävistäjävektori $\pv{AC}$
- lävistäjävektori $\pv{DB}$
- lävistäjävektori $\pv{BD}$.
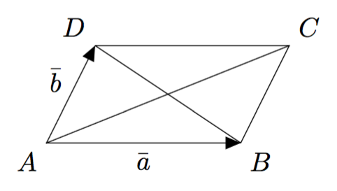
VASTAUS
- $\pv{AC} = \va + \vb$
- $\pv{DB} = \va - \vb$
- $\pv{BD} = \vb - \va$.
Vektoreiden yhteen- ja vähennyslasku
Alla kuvattu monitahokas on suuntaissärmiö, eli sen kaikki tahkot ovat suunnikkaita. Ilmaise sen särmävektoreiden $\va$, $\vb$ ja $\vc$ avulla
- avaruuslävistäjä $\pv{AG}$
- avaruuslävistäjä $\pv{EC}$
- avaruuslävistäjä $\pv{HB}$.
- avaruuslävistäjä $\pv{DF}$.
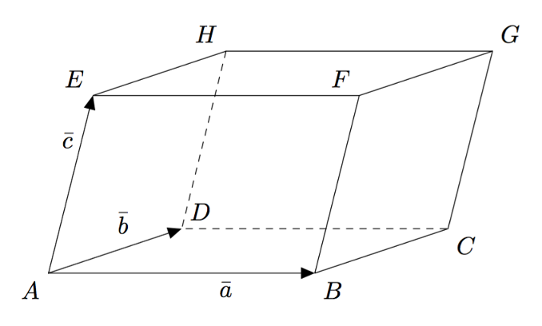
VASTAUS
- $\pv{AG} = \va + \vb + \vc$
- $\pv{EC} = \va + \vb - \vc$
- $\pv{HB} = \va - \vb - \vc$
- $\pv{DF} = \va - \vb + \vc$.
Vektoreiden yhteen- ja vähennyslasku
Tarkastele alla olevaa kuvaa.
- Esitä vektori $\pv{AC}$ vektoreiden $\va$ ja $\vb$ avulla.
- Esitä vektori $\pv{BE}$ vektoreiden $\vb$, $\vc$ ja $\bar{d}$ avulla.
- Esitä vektori $\pv{EC}$ kahdella eri tavalla.
- Laske summa $\va + \vb + \vc + (-\bar{d}) + (-\bar{e})$.
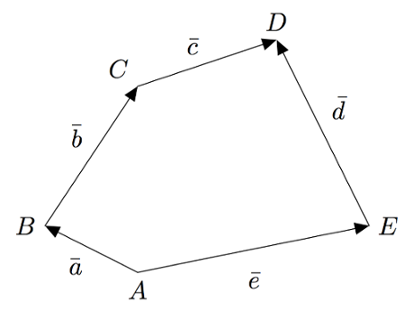
VASTAUS
- $\pv{AC} = \va + \vb$
- $\pv{BE} = \vb + \vc - \bar{d}$
- $\pv{EC} = \bar{d} - \vc$ ja $\pv{EC} = -\bar{e} + \va + \vb$
- Summa on $\bar{0}$.
Joissakin tilanteissa vektorin pituus täytyy muuttaa sopivaksi kertomalla vektoria reaaliluvulla. Esimerkiksi alla olevassa kuvassa piste $C$ jakaa janan $AB$ suhteessa $3:5$. Tällöin $$\pv{AC} = \frac{3}{3+5}\pv{AB} = \frac{3}{8}\pv{AB}.$$
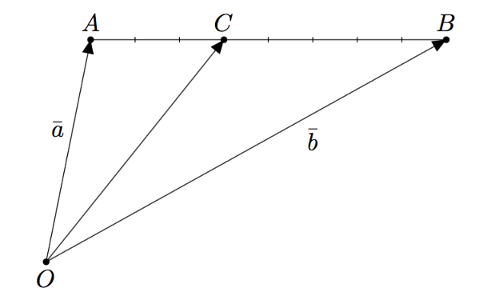
Vektori $\pv{OC}$ saadaan lausuttua vektorien $\va = \pv{OA}$ ja $\vb = \pv{OB}$ avulla, kun etsitään reitti pisteestä $O$ pisteeseen $C$. Tämä voidaan tehdä esimerkiksi kiertämällä pisteen $A$ kautta seuraavasti: $$\begin{align*} \pv{OC} &= \pv{OA} + \pv{AC} \\ &= \pv{OA} + \frac{3}{8}\pv{AB} \\ &= \va + \frac{3}{8}(-\va + \vb) \\ &= \va - \frac{3}{8}\va + \frac{3}{8}\vb \\ &= \frac{5}{8}\va + \frac{3}{8}\vb. \end{align*}$$
Vektorin kertominen reaaliluvulla
Tarkastellaan alla olevaa kuvaa. Edellä lausuttiin vektori $\pv{OC}$ vektorien $\va$ ja $\vb$ avulla etsimällä reitti pisteestä $O$ pisteen $A$ kautta pisteeseen $C$.

Lausu vektori $\pv{OC}$ vektorien $\va$ ja $\vb$ avulla etsimällä reitti pisteestä $O$ pisteen $B$ kautta pisteeseen $C$. Saatko saman tuloksen kuin edellä?
Vektorin kertominen reaaliluvulla
Kolmion $ABC$ sivuvektorit ovat $\va = \pv{AB}$ ja $\vb = \pv{AC}$. Piste $D$ on sivun $BC$ keskipiste. Piirrä tilanteesta mallikuva ja ilmaise vektoreiden $\va$ ja $\vb$ avulla
- sivuvektori $\pv{BC}$
- vektori $\pv{BD}$
- keskijanavektori $\pv{AD}$.
VASTAUS
- $\pv{BC} = \vb - \va$
- $\pv{BD} = \frac{1}{2}(\vb - \va)$
- $\pv{AD} = \frac{1}{2}\va + \frac{1}{2}\vb$.
Vektorin pituus
Tiedetään, että vektorit $\vv$ ja $\vw$ ovat yksikkövektoreita eli niiden pituus on yksi. Määritä vektorin $4\vv+6\vw$ pituus, jos vektorit $\vv$ ja $\vw$ ovat
- samansuuntaiset
- vastakkaissuuntaiset
- kohtisuorassa toisiaan vastaan.
VASTAUS
- $|4\vv+6\vw| = 10$
- $|4\vv+6\vw| = 2$
- $|4\vv+6\vw| = \sqrt{52} = 2\sqrt{13}$.
Joskus vektorin pituuden selvittämiseen voidaan käyttää pistetuloa ja sen ominaisuuksia. Tätä harjoitellaan seuraavassa tehtävässä.
Vektorin pituus
Tiedetään, että $|\va| = 3$, $|\vb| = 5$ ja $\sphericalangle(\va,\vb) = 120^\circ$. Tehtävänä on selvittää vektorin $2\va + \vb$ pituus $|2\va + \vb|$.
- Piirrä tilanteesta mallikuva.
- Havainnollista piirroksella vektoria $2\va + \vb$.
- Sievennä pistetulo $(2\va + \vb) \cdot (2\va + \vb)$. Muista, että pistetulossa sulut voidaan kertoa auki tavalliseen tapaan. (Pistetulon laskusääntöjä löydät $xy$-koordinaatistoa käsittelevän luvun teoreemasta 3.)
- Teoreeman 4 mukaan $\vv \cdot \vv = |\vv|^2$ ja teoreeman 5 mukaan $\vv \cdot \vw = |\vv||\vw|\cos(\vv, \vw)$. Käytä näitä tietoja ja ilmaise c-kohdan tulos vektoreiden $\va$ ja $\vb$ itseisarvojen avulla.
- Käytä tehtävänannon tietoja ja laske edellisen kohdan avulla lukuarvo pistetulolle $(2\va + \vb) \cdot (2\va + \vb)$.
- Sovella tietoa $\vv \cdot \vv = |\vv|^2$ uudelleen ja päättele edellisen kohdan avulla, mikä on vektorin $2\va + \vb$ pituus $|2\va + \vb|$.
VASTAUS
- $4 (\va \cdot \va) + 4(\va \cdot \vb) + \vb\cdot \vb$
- $4 |\va|^2 + 4|\va||\vb|\cos(\va, \vb) + |\vb|^2$
- $31$
- $\sqrt{31}$.
Oletetaan, että $\vv \neq \bar{0}$, $\vw \neq \bar{0}$ ja $\vv \nparallel \vw$. Palautetaan mieleen, että jos vektori $\va$ voidaan kirjoittaa muodossa $$\va = s\vv + t\vw$$ missä $s$ ja $t$ ovat reaalilukuja, niin sanotaan, että $s\vv$ ja $t\vw$ ovat vektorin $\va$ vektoreiden $\vv$ ja $\vw$ suuntaiset komponentit. Tätä on havainnollistettu alla olevassa kuvassa.
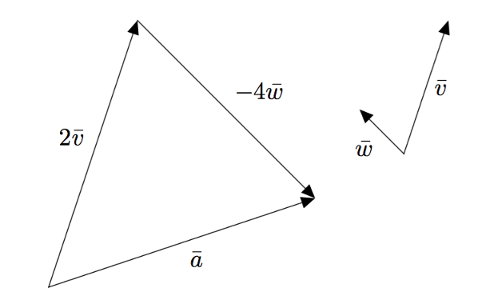
Seuraavan teoreeman mukaan mikä tahansa vektori voidaan jakaa vektoreiden $\vv$ ja $\vw$ suuntaisiin komponentteihin enintään yhdellä tavalla.
TEOREEMA
Oletetaan, että $\vv \neq \bar{0}$, $\vw \neq \bar{0}$ ja $\vv \nparallel \vw$. Jos $s\vw + t\vv = p\vw + q\vv$, niin $s = p$ ja $t = q$.
Perustelu: Oletetaan, että $$s\vw + t\vv = p\vw + q\vv.$$ Lisäämällä yhtälön molemmille puolille $-p\vw - t\vv$ yhtälö saadaan muotoon $$s\vw - p\vw = q\vv - t\vv.$$ Kun yhtälön kummallakin puolella otetaan yhteinen tekijä, saadaan yhtälö muotoon $$(s-p)\vw = (q-t)\vv.$$ Jos kerroin $s-p \neq 0$, saadaan ratkaistua $$\vw = \frac{q-t}{s-p}\vv.$$ Tämä tarkoittaa, että $\vw \parallel \vv$ (tapauksessa, jossa $q-t \neq 0$) tai $\vw = \bar{0}$ (tapauksessa, jossa $q-t = 0$). Tämä on mahdotonta, koska oletuksen mukaan $\vw \neq \bar{0}$ ja $\vv \nparallel \vw$. Siis $s-p = 0$.
Yhtälö saa nyt siis muodon $$0\vw = (q-t)\vv$$ eli $$(q-t)\vv = \bar{0}.$$ Jos kerroin $q-t \neq 0$, saadaan tästä ratkaistua $$\vv = \frac{1}{q-t}\bar{0} = \bar{0}.$$ Tämä on mahdotonta, koska oletuksen mukaan $\vv \neq \bar{0}$. Siis $q-t = 0$.
Koska $s-p = 0$ ja $q-t = 0$, niin $s = p$ ja $q = t$.
Edellistä teoreemaa voidaan hyödyntää tilanteissa, joissa on mahdollista muodostaa jokin vektori annettujen vektoreiden avulla kahta eri reittiä. Tällä tavalla voidaan ratkaista erilaisia geometrisia ongelmia. Tätä havainnollistetaan seuraavassa esimerkissä.
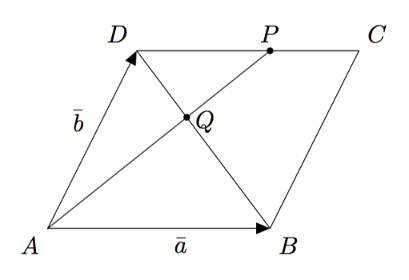
Tarkastellaan yllä olevaa kuvaa. Selvitetään, missä suhteessa piste $Q$ jakaa lävistäjän $BD$, kun tiedetään, että piste $P$ jakaa sivun $DC$ suhteessa $3:2$.
Piste $Q$ on sekä janalla $AP$ että lävistäjällä $BD$, joten vektori $\pv{AQ}$ voidaan muodostaa kahta eri reittiä vektoreiden $\va$ ja $\vb$ avulla.
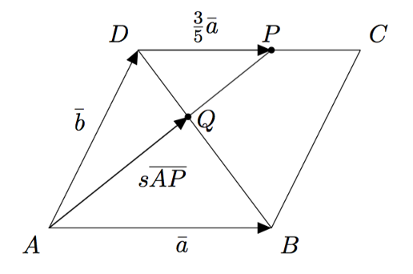
Koska piste $Q$ on janalla $AP$, vektorit $\pv{AQ}$ ja $\pv{AP}$ ovat yhdensuuntaiset. Siten on olemassa luku $s$, jolla $$\pv{AQ} = s\pv{AP}.$$ Vektori $\pv{AP}$ voidaan puolestaan kirjoittaa summana $$\pv{AP} = \pv{AD} + \pv{DP}.$$ Koska piste $P$ jakaa sivun $DC$ suhteessa $3:2$, on $$\begin{align*} \pv{DP} &= \frac{3}{3+2} \pv{DC} = \frac{3}{5}\va. \end{align*}$$ Yhdistämällä kaikki edelliset tiedot saadaan $$\begin{align*} \pv{AQ} &= s\pv{AP} \\ &= s(\pv{AD} + \pv{DP}) \\ &= s(\vb + \frac{3}{5}\va) \\ &= \frac{3}{5}s\va + s\vb. \end{align*}$$
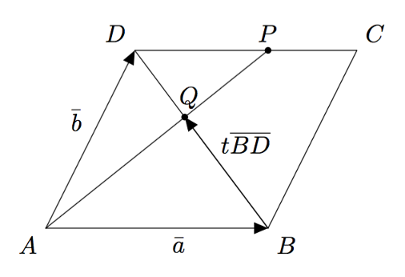
Koska piste $Q$ on lävistäjällä $BD$, vektorit $\pv{BQ}$ ja $\pv{BD}$ ovat yhdensuuntaiset. Siten on olemassa luku $t$, jolla $$\pv{BQ} = t\pv{BD}.$$ Vektori $\pv{BD}$ voidaan puolestaan kirjoittaa summana $$\begin{align*} \pv{BD} &= \pv{BA} + \pv{AD} \\ &= -\va + \vb \\ &= \vb - \va. \end{align*}$$ Muodostetaan näiden tietojen avulla vektori pisteestä $A$ pisteeseen $Q$: $$\begin{align*} \pv{AQ} &= \pv{AB} + \pv{BQ} \\ &= \va + t\pv{BD} \\ &= \va + t(\vb - \va) \\ &= \va + t\vb - t\va \\ &= (1-t)\va + t\vb. \end{align*}$$
Näin on saatu muodostettua vektori $\pv{AQ}$ kahta eri reittiä vektoreiden $\va$ ja $\vb$ avulla. Nyt tiedetään, että $\pv{AQ} = \frac{3}{5}s\va + s\vb$ ja $\pv{AQ} = (1-t)\va + t\vb$. Siis $$\frac{3}{5}s\va + s\vb = (1-t)\va + t\vb.$$ Edellisen teoreeman mukaan tästä yhtälöstä seuraa, että $$ \left\{\begin{aligned} \frac{3}{5}s &= 1-t \\ s &= t. \end{aligned}\right. $$ Kun ylempään yhtälöön sijoitetaan $s = t$, se saa muodon $$\frac{3}{5}t = 1-t$$ lisäämällä molemmille puolille $t$ se saadaan muotoon $$\frac{8}{5}t = 1.$$ Siis $$t = \frac{5}{8}.$$ Koska $$\pv{BQ} = t\pv{BD} = \frac{5}{8}\pv{BD},$$ voidaan päätellä, että jana $BD$ voidaan jakaa kahdeksaan osaan, joista viisi muodostaa janan $BQ$ ja kolme muodostaa janan $QD$. Piste $Q$ jakaa siis janan $BD$ suhteessa $5:3$.
Keskijanavektori
Tehtävänä on selvittää, miten janan keskipisteeseen piirretty vektori saadaan lausuttua janan päätepisteisiin piirrettyjen vektoreiden avulla.
- Piirrä jana $AB$ ja sen ulkopuolelle piste $O$. Merkitse janan $AB$ keskipistettä kirjaimella $M$.
- Piirrä vektorit $\va = \pv{OA}$, $\vb = \pv{OB}$ ja $\pv{OM}$.
- Ilmaise vektori $\pv{AB}$ vektoreiden $\va$ ja $\vb$ avulla.
- Ilmaise vektori $\pv{AM}$ vektorin $\pv{AB}$ avulla.
- Ilmaise vektori $\pv{OM}$ vektoreiden $\va$ ja $\vb$ avulla etsimällä reitti pisteestä $O$ pisteeseen $M$. Edellisten kohtien tuloksista on apua.
- Muotoile omin sanoin teoreema, jonka todistit tässä tehtävässä.
VASTAUS
- $\pv{AB} = \vb - \va$
- $\pv{AM} = \frac{1}{2}\pv{AB}$
- $\pv{OM} = \frac{1}{2}\va + \frac{1}{2}\vb$.
Geometriaa vektoreiden avulla
Tehtävänä on osoittaa, että kolmion kaikki keskijanat leikkaavat toisensa samassa pisteessä ja tämä piste jakaa jokaisen keskijanan kolmion kärjestä lukien suhteessa $2:1$.
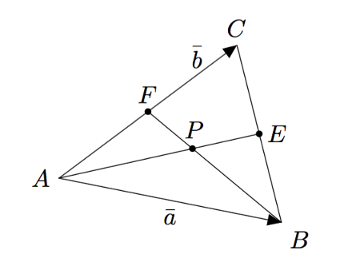
- Piirrä vihkoosi kolmio $ABC$ ja sille kaksi keskijanaa samaan tapaan kuin yllä olevassa kuvassa. Merkitään näiden keskijanojen leikkauspistettä kirjaimella $P$. Merkitään lisäksi $\va = \pv{AB}$ ja $\vb = \pv{AC}$.
- Ilmaise keskijanavektori $\pv{AE}$ vektoreiden $\va$ ja $\vb$ avulla. (Piste $E$ on siis kolmion sivun $BC$ keskipiste.)
- Ilmaise vektori $\pv{AP}$ vektoreiden $\va$ ja $\vb$ avulla hyödyntämällä tietoa, että $\pv{AP} \parallel \pv{AE}$.
- Ilmaise keskijanavektori $\pv{BF}$ vektoreiden $\va$ ja $\vb$ avulla.
- Ilmaise vektori $\pv{AP}$ vektoreiden $\va$ ja $\vb$ avulla etsimällä reitti pisteestä $A$ pisteen $B$ kautta pisteeseen $P$. Edellisen kohdan tuloksesta on apua.
- Nyt sinulla on kaksi esitystä vektorille $\pv{AP}$ vektoreiden $\va$ ja $\vb$ avulla. Muodosta niistä yhtälö ja ratkaise se teoreeman 11 avulla.
- Missä suhteessa piste $P$ jakaa janan $AE$? Entä missä suhteessa piste $P$ jakaa janan $BF$?
- Olisiko tulos ollut erilainen, jos olisit käyttänyt keskijanan $BF$ sijaan kärjestä $C$ lähtevää keskijanaa?
VASTAUS
- $\pv{AE} = \frac{1}{2}\va + \frac{1}{2}\vb$
- $\pv{AP} = t(\frac{1}{2}\va + \frac{1}{2}\vb)$
- $\pv{BF} = -\va + \frac{1}{2}\vb$
- $\pv{AP} = \va + s(-\va + \frac{1}{2}\vb)$
- $t(\frac{1}{2}\va + \frac{1}{2}\vb) = \va + s(-\va + \frac{1}{2}\vb)$, ratkaisuksi saadaan $s = \frac{2}{3} = t$.
- Piste $P$ jakaa janan $AE$ suhteessa $2:1$ ja janan $BF$ suhteessa $2:1$.
Seuraavassa tehtävässä tutkitaan tetraedriä eli nelitahokasta.
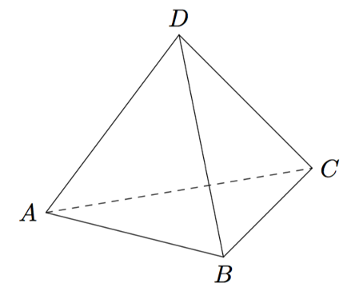
Geometriaa vektoreiden avulla
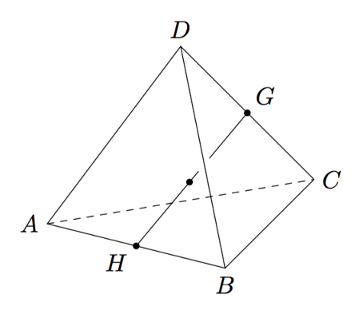
Yhdistetään tetraedrin vastakkaisten särmien keskipisteet janalla kuten alla olevassa kuvassa. Merkitään tämän yhdysjanan keskipistettä kirjaimella $P$.
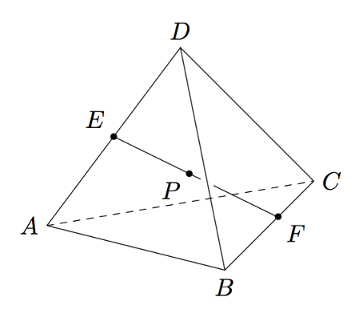
Ajatellaan, että jossain tetraedrin ulkopuolella on piste $O$ ja merkitään $\va = \pv{OA}$, $\vb = \pv{OB}$, $\vc = \pv{OC}$ ja $\bar{d} = \pv{OD}$. Tehtävänä on lausua vektori $\pv{OP}$ vektoreiden $\va$, $\vb$, $\vc$ ja $\bar{d}$ avulla.
- Piirrä vihkoosi yllä oleva kuva ja lisää siihen jonnekin tetraedrin ulkopuolelle piste $O$.
- Ilmaise vektori $\pv{OE}$ vektoreiden $\va$ ja $\bar{d}$ avulla. Hyödynnä edellisen tehtävän tulosta. Voit varmistaa tuloksen oikeellisuuden tämän tehtävän alapuolelta teoreemasta 12.
- Ilmaise vektori $\pv{OF}$ vektoreiden $\vb$ ja $\vc$ avulla.
- Ilmaise vektori $\pv{OP}$ vektoreiden $\pv{OE}$ ja $\pv{OF}$ avulla.
- Yhdistä edellisten kohtien tulokset ja ilmaise vektori $\pv{OP}$ vektoreiden $\va$, $\vb$, $\vc$ ja $\bar{d}$ avulla.
- Olisiko tulos ollut erilainen, jos kysymyksessä olisi ollut joidenkin toisten vastakkaisten särmien keskipisteitä yhdistävän janan keskipiste kuten alla olevassa kuvassa?
- Leikkaavatko tetraedrin vastakkaisten särmien keskipisteitä yhdistävät janat toisensa? Jos leikkaavat, niin missä pisteessä?
VASTAUS
- $\pv{OE} = \frac{1}{2}\va + \frac{1}{2}\bar{d}$
- $\pv{OF} = \frac{1}{2}\vb + \frac{1}{2}\vc$
- $\pv{OP} = \frac{1}{2}\pv{OE} + \frac{1}{2}\pv{OF}$
- $\pv{OP} = \frac{1}{4}\va + \frac{1}{4}\vb + \frac{1}{4}\vc + \frac{1}{4}\bar{d}$
- Tulos olisi ollut sama, vaikka siihen olisi päädytty vähän eri tavalla.
- Kyllä, nämä janat leikkaavat toisensa yhdysjanojen keskipisteessä.
TEOREEMA
Janan keskipisteeseen piirretty vektori on puolet janan päätepisteisiin piirrettyjen vektorien summasta. Alla olevan kuvan merkinnöillä $$\bar{m} = \frac{1}{2}(\va + \vb).$$
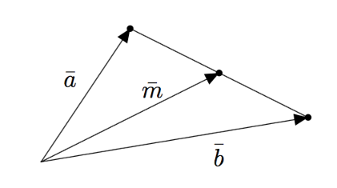
Perustelu: Teoreema on perusteltu tehtävässä 8.
Vektoreiden yhdensuuntaisuuteen liittyvissä kysymyksissäkin saatetaan tarvita teoreemaa 11. Seuraava tehtävä on esimerkki tällaisesta tilanteesta.
Vektoreiden yhdensuuntaisuus
Tiedetään, että vektorit $\vv$ ja $\vw$ eivät ole yhdensuuntaisia eli $\vv \nparallel \vw$. Tehtävänä on määrittää sellainen luku $k$, että vektorit $2\vv + 3\vw$ ja $5\vv + k\vw$ ovat yhdensuuntaiset.
- Millä ehdolla vektorit $2\vv + 3\vw$ ja $5\vv + k\vw$ ovat yhdensuuntaiset? Kertaa tarvittaessa yhdensuuntaisuuden määritelmä $xy$-koordinaatistoa käsittelevästä luvusta.
- Edellisessä kohdassa muodostit yhdensuuntaisuuden määritelmän avulla yhtälön. Muokkaa tätä yhtälöä niin, että saat muodostettua siitä yhtälöparin teoreeman 11 avulla.
- Ratkaise yhtälöpari. Mikä on etsitty luku $k$?
- Kun vektorit $2\vv + 3\vw$ ja $5\vv + k\vw$ ovat yhdensuuntaiset, ovatko ne saman- vai vastakkaissuuntaiset?
VASTAUS
- $k = \frac{15}{2} = 7{,}5$
- Samansuuntaiset.
Myös pistetuloa voidaan hyödyntää geometristen väitteiden perusteluissa. Tarkastellaan esimerkiksi suunnikasta, jonka lävistäjät ovat kohtisuorassa toisiaan vastaan.
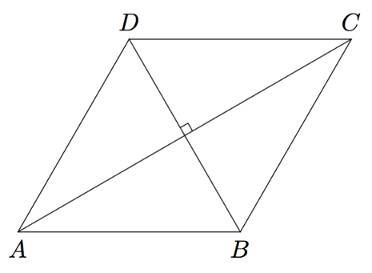
Kuvan perusteella näyttäisi siltä, että suunnikkaan kaikki sivut ovat tässä tapauksessa yhtä pitkiä. Onko kysymys ehkä vain sattumasta? Olisiko mahdollista piirtää suunnikas, jonka lävistäjät ovat kohtisuorassa toisiaan vastaan, mutta jolla on kaksi eri pituista sivua? Seuraavassa tehtävässä tutkitaan tätä asiaa pistetulon avulla.
Geometriaa vektoreiden avulla
Tarkastele alla olevan kuvan suunnikasta $ABCD$.
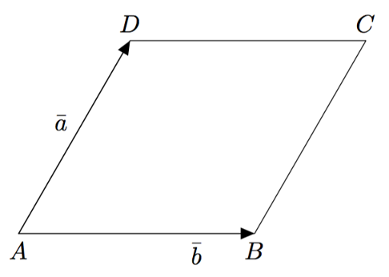
- Ilmaise lävistäjävektorit $\pv{AC}$ ja $\pv{DB}$ vektoreiden $\va$ ja $\vb$ avulla.
- Laske pistetulo $\pv{AC} \cdot \pv{DB}$ edellisen kohdan merkintöjä käyttäen. Muista, että pistetulossa sulut voidaan kertoa auki tavalliseen tapaan. (Pistetulon laskusääntöjä löydät $xy$-koordinaatistoa käsittelevän luvun teoreemasta 3.)
- Kirjoita b-kohdan tulos vektoreiden $\va$ ja $\vb$ itseisarvojen avulla. Tarvittaessa voit tarkistaa teoreemasta 4, miten vektorin pistetulo itsensä kanssa liittyy vektorin itseisarvoon.
- Oletetaan, että suunnikkaan $ABCD$ lävistäjävektorit ovat toisiaan vastaan kohtisuorassa. Mitä voit silloin sanoa lävistäjävektoreiden pistetulosta? Tarvittaessa tarkista asia teoreemasta 6.
- Yhdistä c- ja d-kohtien tiedot. Voitko tästä päätellä, että $|\va|=|\vb|$? Selitä omin sanoin, miten ajattelet.
VASTAUS
- $\pv{AC} = \va + \vb$ ja $\pv{DB} = \vb - \va$
- $\pv{AC} \cdot \pv{DB} = \vb \cdot \vb - \va \cdot \va$
- $\pv{AC} \cdot \pv{DB} = |\vb|^2 - |\va|^2$
- $\pv{AC} \cdot \pv{DB} = 0$
- $|\vb|^2 - |\va|^2 = 0$
TEHTÄVÄSARJA II
Vektoreiden yhteen- ja vähennyslasku
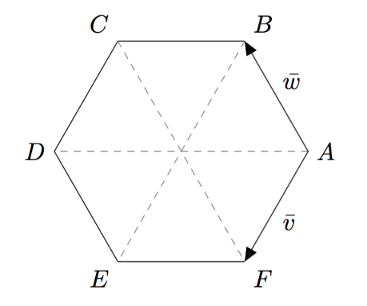
Alla on kuvattuna säännöllinen kuusikulmio $ABCDEF$. Esitä vektoreiden $\vv$ ja $\vw$ avulla
- vektori $\pv{BF}$
- vektori $\pv{BC}$
- vektori $\pv{AC}$
- vektori $\pv{AD}$
- vektori $\pv{BE} + \pv{FC} + \pv{DA}$.
VASTAUS
- $\pv{BF} = \vv - \vw$
- $\pv{BC} = \vv + \vw$
- $\pv{AC} = \vv + 2\vw$
- $\pv{AD} = 2\vv + 2\vw$
- $\pv{BE} + \pv{FC} + \pv{DA} = \bar{0}$.
Vektoreiden yhteen- ja vähennyslasku
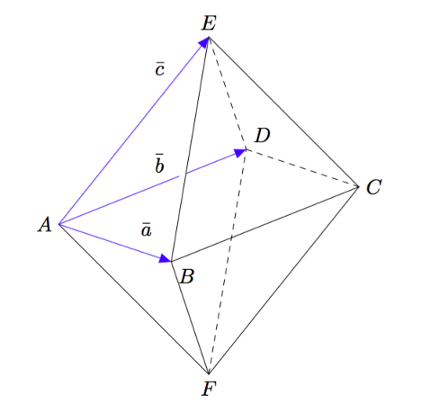
Alla on kuvattuna säännöllinen oktaedri $ABCDEF$. Sen kaikki tahkot ovat tasasivuisia kolmioita. Esitä vektoreiden $\va$, $\vb$ ja $\vc$ avulla
- vektori $\pv{ED}$
- vektori $\pv{AF}$
- vektori $\pv{CE}$
- vektori $\pv{FE}$.
VASTAUS
- $\pv{ED} = \vb - \vc$
- $\pv{AF} = \va + \vb - \vc$
- $\pv{CE} = \vc - \va - \vb$
- $\pv{FE} = 2\vc -\va - \vb$.
Vektoreiden yhteen- ja vähennyslasku
Piirrä kolmio, jonka sivuvektorit $\va$, $\vb$ ja $\vc$ toteuttavat yhtälön
- $\va + \vb + \vc = \bar{0}$
- $\va + \vb - \vc = \bar{0}$
- $\va - \vb - \vc = \bar{0}$.
Vektorin kertominen reaaliluvulla
Missä suhteessa piste $P$ jakaa janan $AB$, jos
- $\pv{AP} = \dfrac{1}{3}\pv{AB}$
- $\pv{AP} = \dfrac{4}{9}\pv{AB}$
- $\pv{AB} = \dfrac{7}{4}\pv{AP}$?
VASTAUS
- $1:2$
- $4:5$
- $4:3$
Vektorin kertominen reaaliluvulla
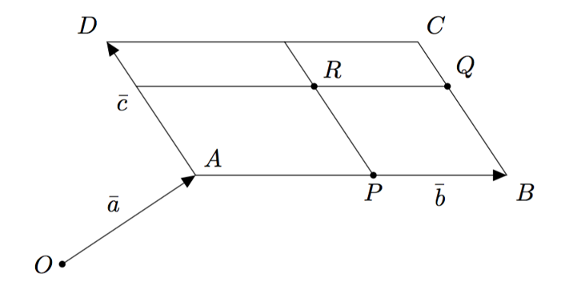
Alla on kuvattu suunnikas $ABCD$. Piste $P$ jakaa sivun $AB$ suhteessa $4:3$ ja piste $Q$ jakaa sivun $BC$ suhteessa $2:1$. Pisteiden $P$ ja $Q$ kautta on piirretty janat, jotka ovat yhdensuuntaiset suunnikkaan sivujen kanssa. Ilmaise vektoreiden $\va$, $\vb$ ja $\vc$ avulla
- vektori $\pv{OP}$
- vektori $\pv{OQ}$
- vektori $\pv{OR}$.
VASTAUS
- $\pv{OP} = \va + \frac{4}{7}\vb$
- $\pv{OQ} = \va + \vb + \frac{2}{3}\vc$
- $\pv{OR} = \va + \frac{4}{7}\vb + \frac{2}{3}\vc$.
Vektorin komponentit
Tason suuntien ilmaisemiseen käytettiin vektoreita $\vv$ ja $\vw$, jotka eivät olleet yhdensuuntaisia ($\vv \nparallel \vw$). Pisteestä $A$ kuljettiin ensin suuntaan, joka oli yhdensuuntainen vektorin $\va = 4\vv - 3\vw$ kanssa. Sen jälkeen liikuttiin suuntaan, joka oli yhdensuuntainen vektorin $\vb = 5\vv - 2\vw$ kanssa. Näin päädyttiin sellaiseen pisteeseen $B$, että $\pv{AB} = -10\vv - 3\vw$. Määritä ne kaksi vektoria, jotka muodostivat kuljetun reitin.
VASTAUS
Kuljetut vektorit olivat $20\vv - 15\vw$ ja $-30\vv + 12\vw$.
Vektorin kertominen reaaliluvulla
Oletetaan, että kumpikaan vektoreista $\vv$ ja $\vw$ ole nollavektori. Oletetaan lisäksi, että $\vw-3\vv=5(\vv-\vw)$. Perustele näiden tietojen avulla, että vektorit $\vv$ ja $\vw$ ovat yhdensuuntaiset. Ovatko ne saman- vai vastakkaissuuntaiset?
VASTAUS
Vektorit $\vv$ ja $\vw$ ovat samansuuntaiset, sillä $\vw = \frac{4}{3}\vv$.
Vektoreiden yhdensuuntaisuus
Tiedetään, että vektorit $\va$ ja $\vb$ eivät ole yhdensuuntaisia eli $\va \nparallel \vb$. Määritä kaikki luvut $k$, joilla vektorit $3\va + k\vb$ ja $4k\va + 3\vb$ ovat yhdensuuntaiset.
VASTAUS
$k = \pm\frac{3}{2}$
Geometriaa vektoreiden avulla
Tehtävänä on osoittaa, että suunnikkaan lävistäjät puolittavat toisensa.
- Piirrä vihkoosi mallikuva suunnikkaasta $ABCD$. Anna sen sivuvektoreille nimeksi $\va$ ja $\vb$.
- Ilmaise suunnikkaan lävistäjävektorit vektoreiden $\va$ ja $\vb$ avulla.
- Olkoon lävistäjien leikkauspiste $P$. Ilmaise vektori $\pv{AP}$ kahta erilaista reittiä vektoreiden $\va$ ja $\vb$ avulla.
- Muodosta tilanteesta yhtälö ja ratkaise se teoreeman 11 avulla.
- Missä suhteessa piste $P$ jakaa lävistäjän $AC$? Entä lävistäjän $BD$? Selitä omin sanoin, mistä tämä nähdään.
VASTAUS
- Esimerkiksi $\va + \vb$ ja $\va - \vb$.
- Esimerkiksi $\pv{AP} = t(\va + \vb)$ ja $\pv{AP} = \vb + s(\va - \vb)$.
- Ratkaisuksi saadaan $s = \frac{1}{2}$ ja $t = \frac{1}{2}$
- Piste $P$ jakaa lävistäjän $AC$ suhteessa $1:1$, samoin lävistäjän $BD$.
Vektorin pituus ja pistetulo
Tiedetään, että vektorin pistetulo itsensä kanssa on sama kuin sen pituuden neliö eli $\va \cdot \va = |\va|^2$.
- Muokkaa tämän tiedon ja pistetulon laskusääntöjen avulla lauseke $|\vv + \vw|^2$ muotoon, jossa näkyy vektorin $\vv$ pituus $|\vv|$ ja vektorin $\vw$ pituus $|\vw|$.
- Mikä on vektorin $\vv + \vw$ pituus, jos $|\vv|=7, |\vw|=5$ ja $\vv\cdot \vw = 1$? Edellisestä kohdasta on apua.
VASTAUS
- $|\vv + \vw|^2 = |\vv|^2 + 2(\vv \cdot \vw) + |\vw|^2$
- $|\vv + \vw| = \sqrt{72} = 2\sqrt{19}$.
Vektorin pituus ja pistetulo
Tiedetään, että $|\va| = 5$ ja $|\vb| = 9$. Vektoreiden $\va$ ja $\vb$ välinen kulma on $\sphericalangle(\va,\vb)= 72^\circ$.
- Laske vektorin $\va-\vb$ pituus.
- Laske vektorin $\va+\vb$ pituus.
Piirrä tilanteesta mallikuva ja käytä sitä apuna tehtävän ratkaisussa. Anna vastaukset kahden merkitsevän numeron tarkkuudella.
VASTAUS
- $|\va-\vb| \approx 8{,}8$; tarkka arvo $\sqrt{\frac{257 - 45\sqrt{5}}{2}}$
- $|\va + \vb| \approx 11{,}6$; tarkka arvo $\sqrt{\frac{167 + 45\sqrt{5}}{2}}$.
Geometriaa vektoreiden avulla
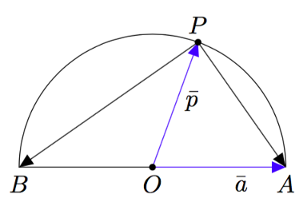
Tehtävänä on osoittaa, että puoliympyrän sisältämä kehäkulma on suora kulma. Alla olevassa kuvassa on näkyvissä yksi puoliympyrän sisältämä kehäkulma $\sphericalangle(\pv{PA},\pv{PB})$. Piste $O$ on ympyrän keskipiste.
- Ilmaise vektorit $\pv{PA}$ ja $\pv{PB}$ vektoreiden $\va = \pv{OA}$ ja $\bar{p} = \pv{OP}$ avulla.
- Sievennä pistetulo $\pv{PA} \cdot \pv{PB}$ pistetulon ominaisuuksien avulla.
- Mistä tiedät, että vektorit $\va$ ja $\bar{p}$ ovat yhtä pitkiä? Selitä omin sanoin.
- Mistä tiedät, että vektorit $\pv{PA}$ ja $\pv{PB}$ ovat kohtisuorassa toisiaan vastaan? Selitä omin sanoin.
VASTAUS
- $\pv{PA} = \va - \bar{p}$ ja $\pv{PB} = -\va - \bar{p}$.
- $\pv{PA} \cdot \pv{PB} = |\bar{p}|^2 - |\va|^2$
TEHTÄVÄSARJA III
Perustele, että kolmion kahden sivun keskipisteiden yhdysjana on kolmion kolmannen sivun suuntainen ja pituudeltaan puolet sen pituudesta.
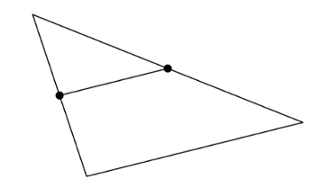
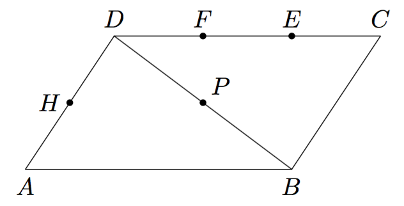
Alla olevan kuvan suunnikkaassa piste $H$ jakaa sivun $AD$ suhteessa $1:1$ ja piste $P$ jakaa lävistäjän $BD$ suhteessa $1:1$. Piste $F$ jakaa sivun $DC$ suhteessa $1:2$ ja piste $E$ suhteessa $2:1$. Merkitään $\vv = \pv{AB}$ ja $\vw = \pv{AD}$. Esitä vektoreiden $\vv$ ja $\vw$ avulla
- vektori $\pv{FH}$
- vektori $\pv{PE}$
- vektori $\pv{FP}$.
VASTAUS
- $\pv{FH} = -\frac{1}{3}\vv - \frac{1}{2}\vw$
- $\pv{PE} = \frac{1}{6}\vv + \frac{1}{2}\vw$
- $\pv{FP} = \frac{1}{6}\vv - \frac{1}{2}\vw$.
Suunnikkaassa $ABCD$ piste $P$ on sivun $CD$ keskipiste ja piste $Q$ jakaa lävistäjän $BD$ suhteessa $1:2$. Perustele, että janat $AP$ ja $CQ$ ovat yhdensuuntaiset.
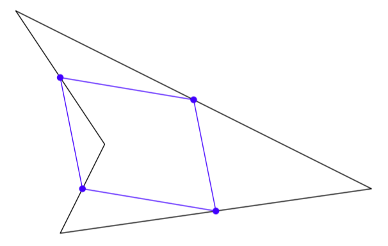
Nelikulmion $ABCD$ sivujen keskipisteet yhdistetään toisiinsa janoilla kuten alla olevassa kuvassa. Osoita, että syntyvä nelikulmio $PQRS$ on aina suunnikas.
Suunnikkaan kärkipiste yhdistetään kahdella janalla vastakkaisten sivujen keskipisteisiin. Osoita, että nämä yhdysjanat jakavat leikkaamansa suunnikkaan lävistäjän kolmeen yhtä pitkään osaan.
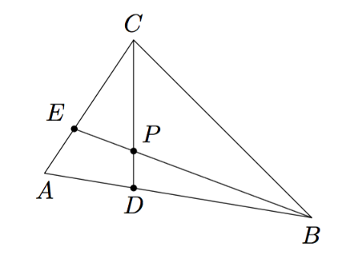
Piste $D$ jakaa kolmion $ABC$ sivun $AB$ suhteessa $1:2$ ja piste $E$ sivun $AC$ samassa suhteessa $1:2$. Perustele, että janojen $BE$ ja $CD$ leikkauspiste $P$ on kolmion kärjestä $A$ piirretyn keskijanan keskipiste.
Osoita, että suuntaissärmiön kaikki avaruuslävistäjät leikkaavat toisensa pisteessä, joka on jokaisen avaruuslävistäjän keskipiste.
Tiedetään, että vektoreista $\va$ ja $\vb$ kumpikaan ei ole nollavektori. Lisäksi tiedetään, että $\va \nparallel \vb$. Onko mahdollista, että $-2\va + 15\vb = \bar{0}$? Selitä, miten ratkaisit tehtävän.
VASTAUS
Ei ole mahdollista, sillä yhtälöstä seuraisi, että $\va = \frac{15}{2}\vb$. Kuitenkin tiedetään, että $\va \nparallel \vb$.
Kolmiosta $ABC$ tiedetään, että sivun $AB$ pituus on 4 ja sivun $AC$ pituus on 6. Kuinka pitkä on sivu $BC$, jos
- pistetulo $\pv{AB} \cdot \pv{AC} = 5$
- pistetulo $\pv{AB} \cdot \pv{AC} = -5$.
VASTAUS
- $|\pv{BC}| = \sqrt{42}$
- $|\pv{BC}| = \sqrt{62}$.
Kolmion $OAB$ sivuvektorit $\va = \pv{OA}$ ja $\vb = \pv{OB}$ toteuttavat ehdon $\va \cdot \va = 2\va \cdot \vb$. Osoita, että kolmio $OAB$ on tasakylkinen. [Pitkä S2008/11]
Itsearviointitehtävät
Varmista, että olet oppinut tämän luvun keskeiset asiat tekemällä itsearviointitesti opetus.tv:n polku-palvelussa. Samalla harjoittelet omien ratkaisujesi pisteyttämistä pisteytysohjeiden avulla.

