Suorakulmainen kolmio tarkoittaa kolmiota, jonka yksi kulma on suora kulma eli $90^\circ$. Esimerkiksi alla oleva kolmio on suorakulmainen kolmio.
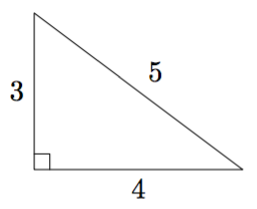
Suorakulmaisen kolmion pisintä sivua sanotaan hypotenuusaksi ja lyhyempiä sivuja kateeteiksi. Esimerkiksi yllä olevan kolmion hypotenuusan pituus on 5 ja kateettien pituudet ovat 3 ja 4.
Tutkitaan seuraavaksi, miten suorakulmaisen kolmion hypotenuusan pituus ja kateettien pituudet liittyvät toisiinsa.
Tehtävän 1.12 tuloksena saadaan seuraava Pythagoraan lauseena tunnettu teoreema:
TEOREEMA
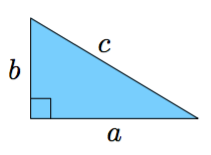
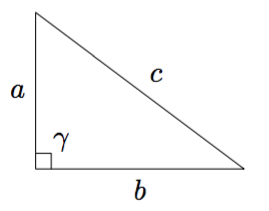
Suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö, eli alla olevan kuvan merkinnöillä $$a^2 + b^2 = c^2$$

Seuraavissa tehtävissä harjoitellaan Pythagoraan lauseen soveltamista.
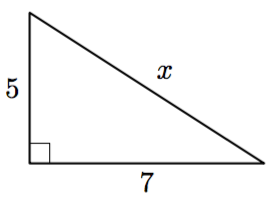
Tehtävänä on selvittää yllä olevan kolmion kolmannen sivun pituus.
- Muodosta kolmion sivujen pituuksien välille Pythagoraan lauseen mukainen yhtälö. Ratkaise tästä yhtälöstä tuntemattoman sivun pituuden neliö eli $x^2$.
- Edellisessä kohdassa olet päätynyt niin sanottuun toisen asteen potenssiyhtälöön $x^2 = s$, joita ratkaistiin edellisessä kurssissa. Jos vakio $s$ on positiivinen eli $s > 0$, tällä yhtälöllä on kaksi ratkaisua. Mitkä nämä ratkaisut ovat a-kohdan yhtälön tapauksessa? Selitä omin sanoin, miksi vain toinen niistä voi olla kysytty kolmion sivun pituus.
- Mikä on yllä olevan kolmion kolmannen sivun pituus? Anna vastauksen tarkka arvo ja likiarvo kahden merkisevän numeron tarkkuudella.
-
-
- $x = \sqrt{74} \approx 8{,}6$.
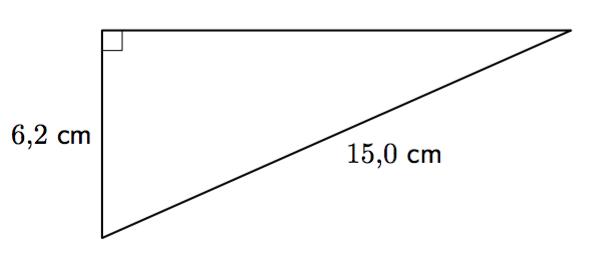
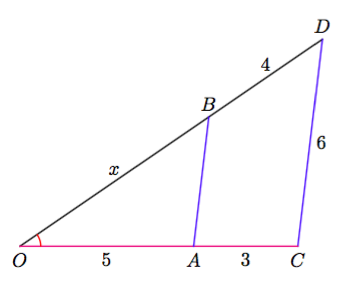
Tehtävänä on selvittää yllä olevan kolmion kolmannen sivun pituus.
- Merkitse tuntemattoman sivun pituutta jollakin kirjaimella. Muodosta kolmion sivujen pituuksien välille Pythagoraan lauseen mukainen yhtälö. Ratkaise tästä yhtälöstä tuntemattoman sivun pituuden neliö.
- Edellisessä kohdassa olet jälleen päätynyt niin sanottuun toisen asteen potenssiyhtälöön. Ratkaise tästä yhtälöstä tuntemattoman sivun pituus. Anna vastaus kahden merkisevän numeron tarkkuudella.
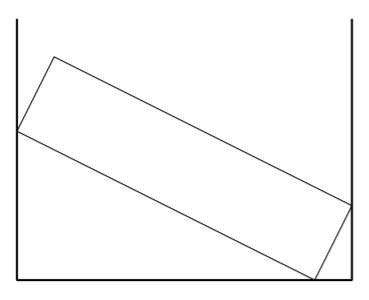
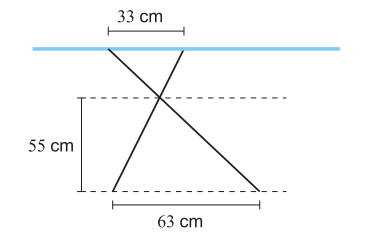
Hissin oviaukon korkeus on 2,00 metriä ja leveys 0,60 metriä. Hissikorin pituus oviaukosta peräseinään on 1,40 metriä. Tehtävänä on selvittää, mahtuuko 2,05 m pitkä ja 1,00 m leveä pöytälevy ovesta hissiin sopivasti kallistettuna.
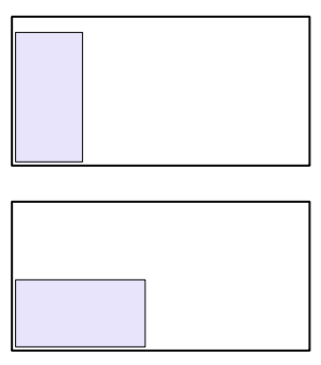
- Piirrä kuva hissin oviaukosta edestäpäin katsottuna. Merkitse piirrokseen oviaukon mitat.
- Missä asennossa pöytälevy kannattaa siirtää hissiin? Täydennä piirrosta ja merkitse pöytälevyn suurinta mahdollista pituutta jollakin kirjaimella.
- Muodosta sopiva yhtälö ja ratkaise pöytälevyn suurin mahdollinen pituus.
- Mahtuuko 2,05 m pitkä ja 1,00 m leveä pöytälevy ovesta hissiin?
-
-
- Hissiin mahtuvan pöytälevyn suurin mahdollinen pituus on $\sqrt{4{,}36} \text{ cm} \approx 2{,}09 \text{ cm}$.
- Teoriassa pitäisi mahtua.
Hissin oviaukon korkeus on 2,00 metriä ja hissikorin pituus oviaukosta peräseinään on 1,40 metriä. Tehtävänä on selvitää, mikä hissin oven leveyden pitäisi vähintään olla, jotta 2,30 m pitkä ja 1,20 metriä leveä kipsilevy mahtuisi hissiin.
- Piirrä kuva hissin oviaukosta edestäpäin katsottuna. Merkitse piirrokseen oviaukon mitat. Merkitse oviaukon leveyttä jollakin kirjaimella.
- Missä asennossa kipsilevy kannattaa siirtää hissiin? Täydennä piirrosta ja merkitse siihen kipsilevyn mitta.
- Muodosta sopiva yhtälö ja ratkaise hissin oven leveys. Mikä on järkevä tarkkuus vastaukselle?
-
-
- Oven vähimmäisleveys on $\sqrt{1{,}29} \text{ m} \approx 1{,}14 \text{ m}$.
Pythagoraan lauseen avulla saadaan aina ratkaistua suorakulmaisen kolmion kolmas sivu, jos kahden sivun pituus tunnetaan. Tutkitaan seuraavaksi, miten voidaan selvittää suorakulmaisen kolmion terävien kulmien suuruus, jos sivujen pituudet tunnetaan.
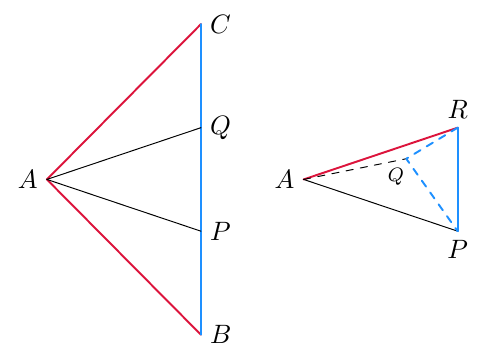
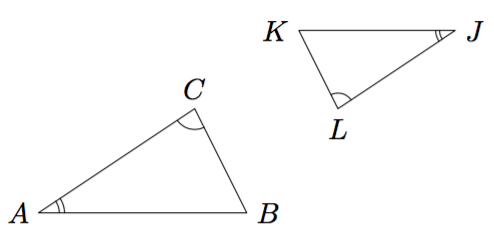
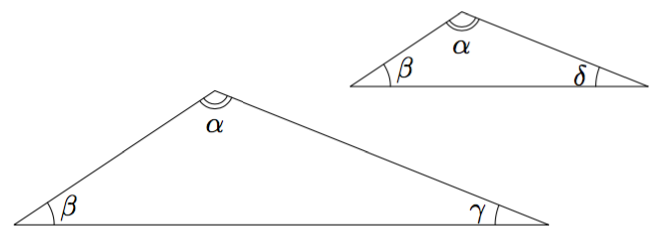
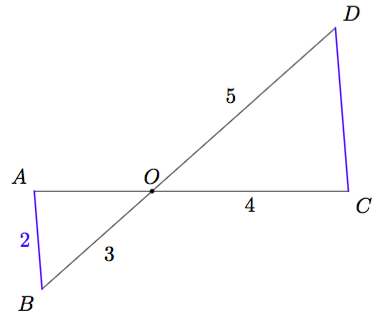
Tarkastellaan kahta suorakulmaista kolmiota, joissa on yhtä suuri terävä kulma $\alpha$.
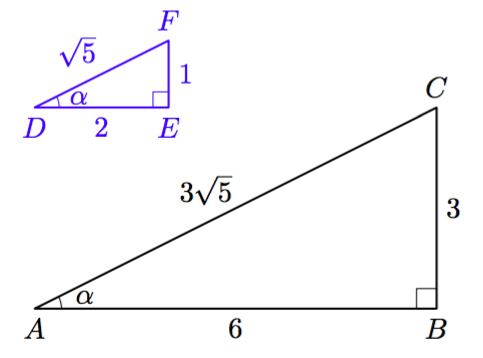
Nämä kolmiot ovat yhdenmuotoiset KK-lauseen (teoreema 3) nojalla, koska niissä on kaksi yhtä suurta kulmaa: suora kulma sekä kulma $\alpha$.
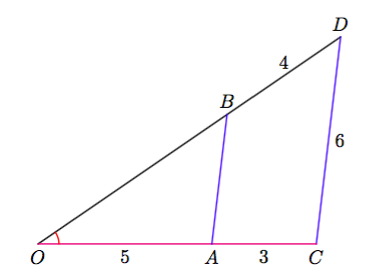
Koska kolmiot ovat yhdenmuotoiset, on suhde $$\frac{\text{ vastinsivun pituus }}{\text{ sivun pituus }}$$ sama riippumatta siitä, mitä kolmion sivua tarkastellaan. Esimerkiksi $$\frac{AB}{\textcolor{blue}{DE}} = \frac{6}{2} = 3$$ ja $$\frac{AC}{\textcolor{blue}{DF}} = \frac{3\sqrt{5}}{\sqrt{5}} = 3.$$ Verrantoyhtälön $$\frac{AB}{\textcolor{blue}{DE}} = \frac{AC}{\textcolor{blue}{DF}}$$ molemmat puolet voidaan kertoa nimittäjien tulolla $\textcolor{blue}{DE} \cdot \textcolor{blue}{DF}$, jolloin saadaan yhtälö $$AB \cdot \textcolor{blue}{DF} = AC \cdot \textcolor{blue}{DE}.$$ Kun tämän yhtälön molemmat puolet jaetaan tulolla $AC \cdot \textcolor{blue}{DF}$, saadaan yhtälö $$\frac{AB}{AC} = \frac{\textcolor{blue}{DE}}{\textcolor{blue}{DF}}.$$ Havaitaan, että kolmion $ABC$ sivujen suhde on sama kuin niiden vastinsivujen suhde kolmiossa $DEF$.

Esimerkiksi edellä tarkasteltu kulman $\alpha$ viereisen kateetin suhde hypotenuusaan on molemmissa kolmioissa sama $$\frac{6}{3\sqrt{5}} = \frac{2}{\sqrt{5}} = \frac{2}{5}\sqrt{5}.$$
Suorakulmaisen kolmion sivujen pituuksien suhteille onkin annettu omat nimensä seuraavan määritelmän mukaisesti:
MÄÄRITELMÄ: SINI, KOSINI JA TANGENTTI
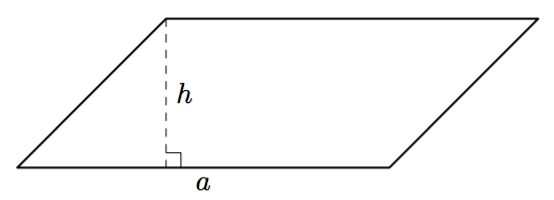
Suorakulmaisessa kolmiossa terävän kulman $\alpha$ sini, kosini ja tangetti tarkoittavat kolmion sivujen pituuksien suhteita: \begin{align*} \sin \alpha &= \dfrac{\text{ kulman vastainen kateetti }}{\text{ hypotenuusa }} \\[2mm] \cos \alpha &= \dfrac{\text{ kulman viereinen kateetti }}{\text{ hypotenuusa }} \\[2mm] \tan \alpha &= \dfrac{\text{ kulman vastainen kateetti }}{\text{ kulman viereinen kateetti }} \end{align*}
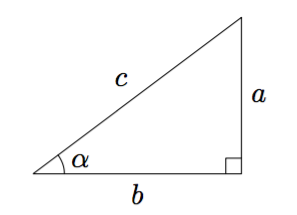
Yllä olevan kuvion merkinnöillä \begin{align*} \sin \alpha &= \dfrac{a}{c} \\[1mm] \cos \alpha &= \dfrac{b}{c} \\[1mm] \tan \alpha &= \dfrac{a}{b} \end{align*}
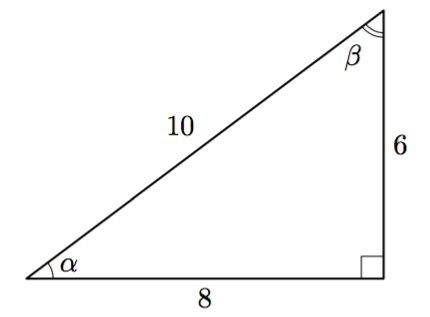
Suorakulmaisen kolmion hypotenuusan pituus on 10 ja kateettien pituudet ovat 6 ja 8 yllä olevan kuvan mukaisesti. Määritä seuraavat sivujen suhteet:
- $\sin \alpha$
- $\cos \alpha$
- $\tan \alpha$
- $\sin \beta$
- $\cos \beta$
- $\tan \beta$
-
-
-
- $\sin \beta = \dfrac{4}{5}$
- $\cos \beta = \dfrac{3}{5}$
- $\tan \beta = \dfrac{4}{3}$
Suorakulmaisessa kolmiossa terävän kulman $\alpha$ tangetti on $5:12$ eli $$\tan \alpha = \frac{5}{12}$$
- Keksi esimerkki suorakulmaisesta kolmiosta, jossa on tällainen terävä kulma. Mitkä ovat keksimäsi suorakulmaisen kolmion kateettien pituudet?
- Laske keksimäsi suorakulmaisen kolmion hypotenuusan pituus.
- Keksi esimerkki toisesta suorakulmaisesta kolmiosta, jossa on samanlainen kulma $\alpha$. Selitä omin sanoin, miten ajattelit.
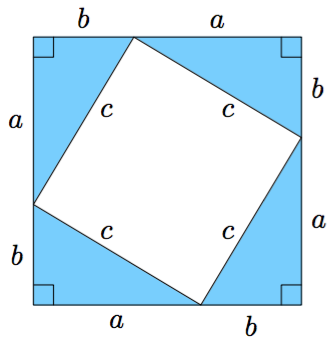
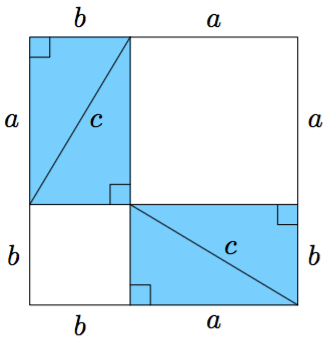
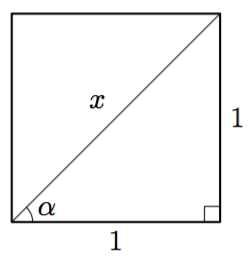
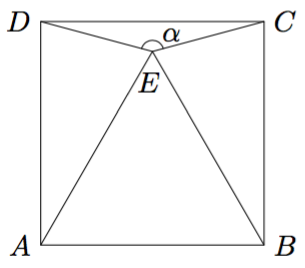
Tarkastele alla olevaa neliötä, joka on jaettu lävistäjällä kahdeksi suorakulmaiseksi kolmioksi.
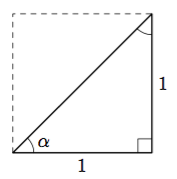
- Laske suorakulmaisen kolmion hypotenuusan pituus.
- Päättele kulman $\alpha$ suuruus kolmion symmetrian avulla.
Vihje: teoreema 2. - Määritä kolmion sivujen pituuksien avulla $\sin \alpha$, $\cos \alpha$ ja $\tan \alpha$.
Edellisen tehtävän perusteella voidaan laatia seuraava taulukko:
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $45^\circ$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{\sqrt{2}}$ | $1$ |
Jokaista terävää kulmaa vastaa yksi sinin, kosinin ja tangentin arvo. Esimerkiksi yllä olevasta taulukosta nähdään, että $$\cos 45^\circ = \dfrac{1}{\sqrt{2}}.$$
Toisaalta jokaista (suorakulmaisessa kolmiossa mahdollista) trigonometristä suhdetta vastaa yksi terävä kulma. Esimerkiksi yllä olevan taulukon avulla voidaan päätellä, että jos $\tan \beta = 1$, niin $\beta = 45^\circ$.
Laskinten ja tietokoneiden avulla tämä siirtyminen kulman ja trigonometristen suhteiden välillä voidaan tehdä ilman taulukoiden käyttöä. Annettua kulmaa vastaava trigonometrinen suhde sini, kosini tai tangentti saadaan laskimella käyttämällä nappulaa $\bbox[3px,border:2px solid black]{\texttt{sin}\phantom{i}}\ $, $\ \bbox[3px,border:2px solid black]{\texttt{cos}\phantom{i}}\ $ tai $\ \bbox[3px,border:2px solid black]{\texttt{tan}\phantom{i}}\ $. Trigonometrista suhdetta vastaava kulma saadaan nappuloilla $\bbox[3px,border:2px solid black]{\texttt{sin}^{-1}}\ $, $\ \bbox[3px,border:2px solid black]{\texttt{cos}^{-1}}\ $ ja $\ \bbox[3px,border:2px solid black]{\texttt{tan}^{-1}}\ $.
Kopioi alla oleva taulukko vihkoosi ja täydennä siihen puuttuvat tiedot laskimen avulla tarkkoina arvoina tai kolmen merkitsevän numeron tarkkuudella:
| Kulma $\alpha$ | $\sin \alpha$ | $\cos \alpha$ | $\tan \alpha$ |
| $10^\circ$ | $\phantom{\dfrac{1}{2}}$ | | |
| | $\dfrac{1}{2}$ | | |
| | | $\dfrac{1}{\sqrt{2}}$ | |
| | $\phantom{\dfrac{1}{2}}$ | | $\sqrt{3}$ |
| $80^\circ$ | $\phantom{\dfrac{1}{2}}$ | | |
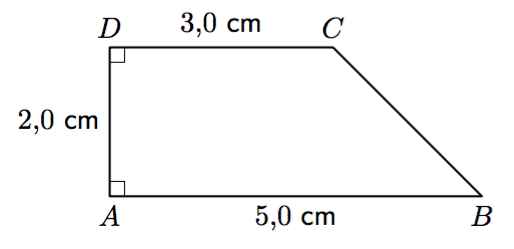
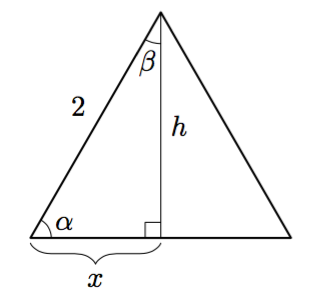
Tarkastele alla olevaa suorakulmaista kolmiota.
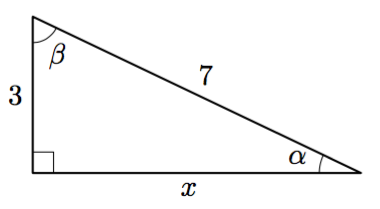
- Selvitä toisen kateetin pituus (tarkka arvo).
- Selvitä kulman $\alpha$ suuruus jonkin trigonometrisen suhteen avulla. Anna vastaus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kulman $\beta$ suuruus.
- $\sqrt{40} = 2\sqrt{10}$
- $\alpha \approx 25{,}4^\circ$
- $\beta \approx 64{,}6^\circ$
Tarkastele alla olevaa suorakulmaista kolmiota.
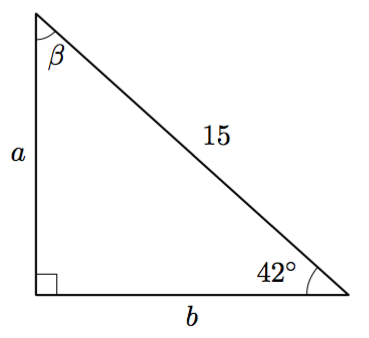
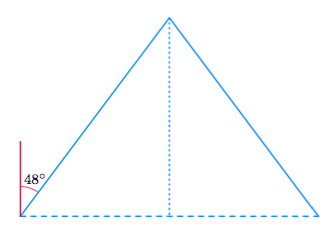
- Ilmaise $\sin 42^\circ$ kolmion sivujen suhteena. Ratkaise tästä yhtälöstä kateetin $a$ pituus kolmen merkitsevän numeron tarkkuudella.
- Ilmaise $\cos 42^\circ$ kolmion sivujen suhteena. Ratkaise tästä yhtälöstä kateetin $b$ pituus kolmen merkitsevän numeron tarkkuudella.
- Selvitä kulman $\beta$ suuruus.
- $a \approx 10{,}0$
- $b \approx 11{,}1$
- $\beta = 48^\circ$
Laskettelurinteen pituus on 1300 metriä ja korkeusero 262 metriä. Tehtävänä on laskea mäen rinteen keskimääräinen kaltevuuskulma (vaakatasoon verrattuna).
- Piirrä mallikuva, jossa rinteen poikkileikkaus sivusta katsottuna on suorakulmainen kolmio. Merkitse kuvaan rinteen mitat.
- Ratkaise rinteen kaltevuuskulma sopivan trigonometrisen suhteen avulla. Anna vastaus kahden merkitsevän numeron tarkkuudella.
-
- Rinteen kaltevuuskulma on noin 12 astetta.

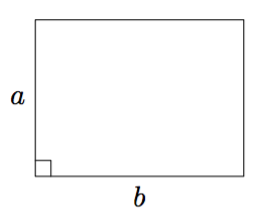



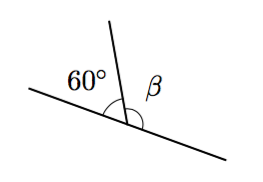
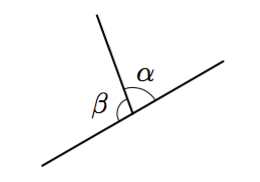
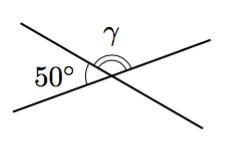
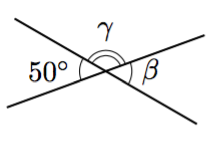
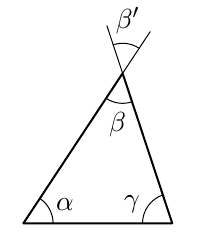
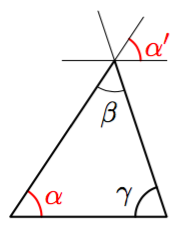
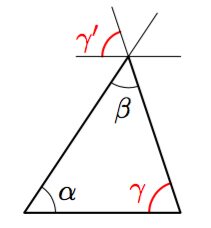
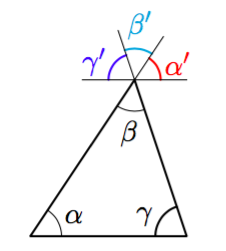






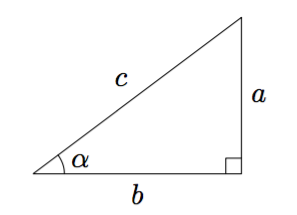















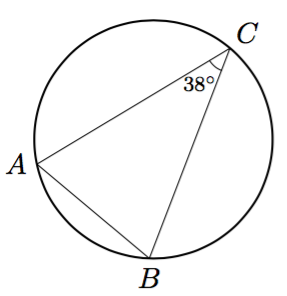 Vinkki: teoreemat 17 sekä 4 tai 8.
Vinkki: teoreemat 17 sekä 4 tai 8. 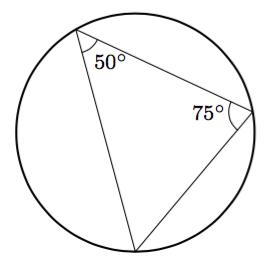
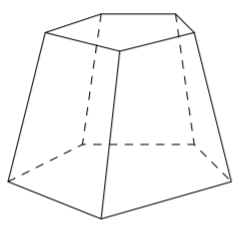
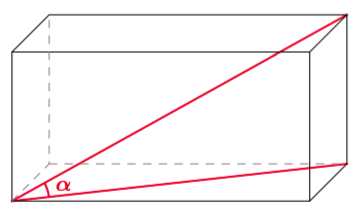
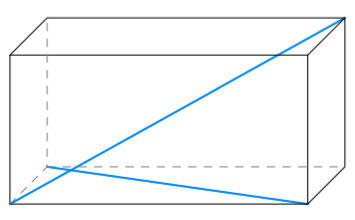
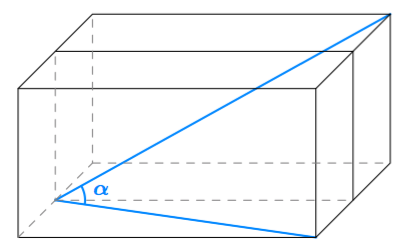
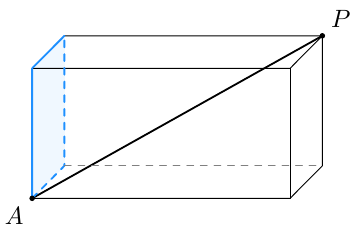
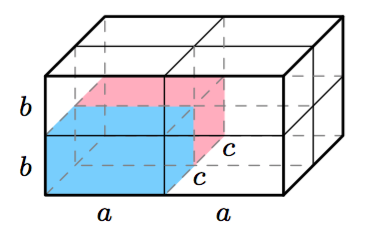
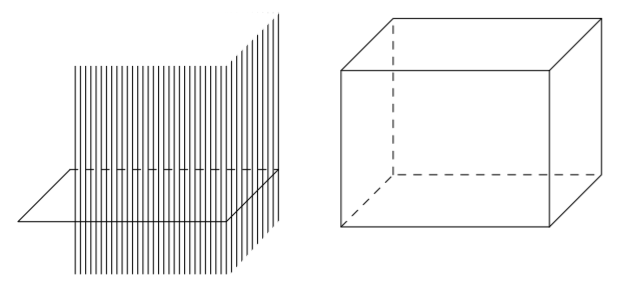
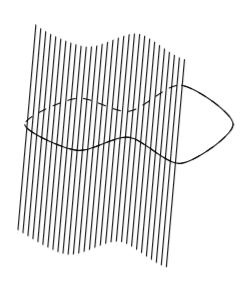
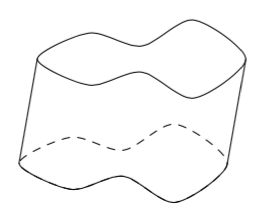
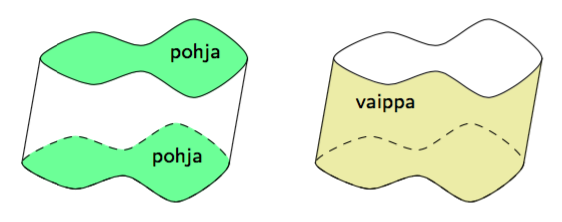
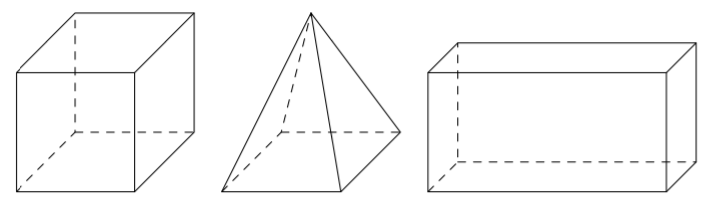 Sovitaan seuraavaksi vielä tarkemmin, mitä tarkoitetaan suorakulmaisella särmiöllä.
Sovitaan seuraavaksi vielä tarkemmin, mitä tarkoitetaan suorakulmaisella särmiöllä. 
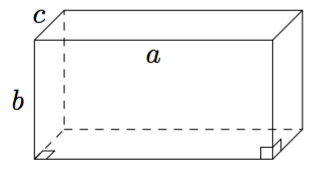
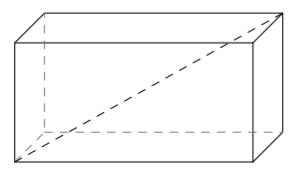
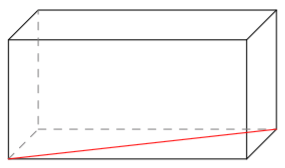
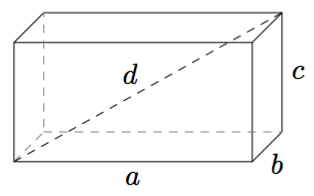

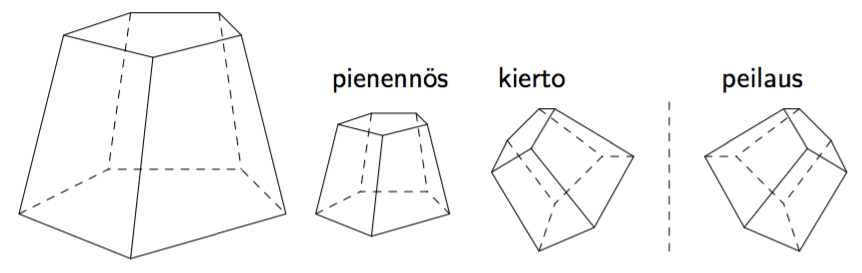
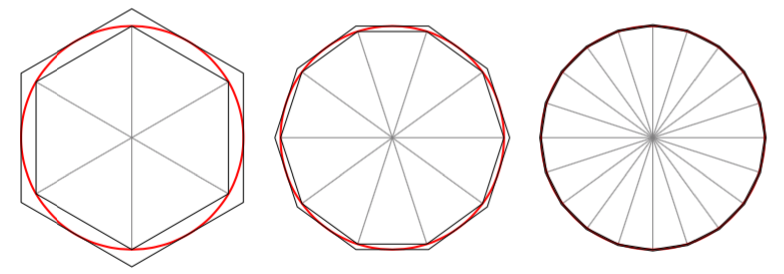
 (Yllä olevat punaiset kuvat Robert Webb,
(Yllä olevat punaiset kuvat Robert Webb,