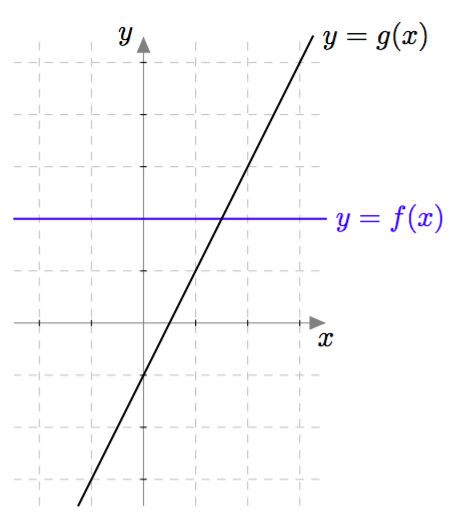
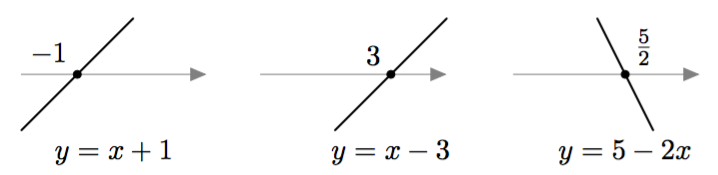Kurssin alkupuolella opeteltiin ratkaisemaan ensimmäisen asteen yhtälöitä eli yhtälöitä, jotka voidaan kirjoittaa muodossa $ax + b = 0$, missä $a \neq 0$. Tällaiseen yhtälöön päädytään esimerkiksi silloin, kun tutkitaan, missä kohdassa ensimmäisen asteen polynomifunktio saa jonkin tietyn arvon. Vastaavasti toisen asteen polynomifunktiota tutkittaessa päädytään niin sanottuun toiseen asteen yhtälöön. Sellaiset opitaan ratkaisemaan tässä kappaleessa.
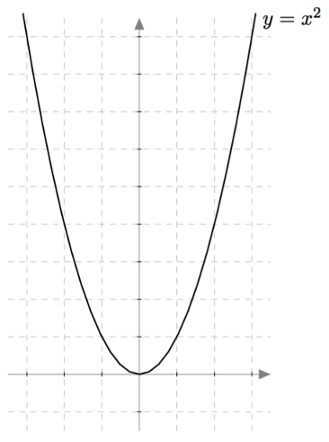
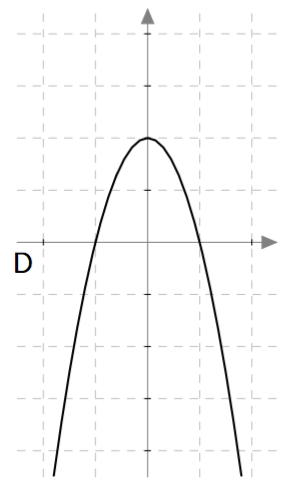
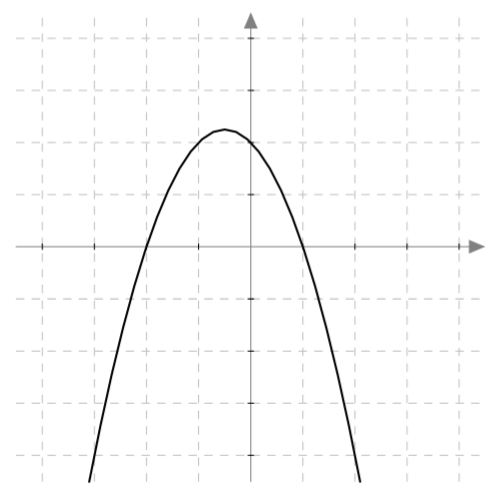
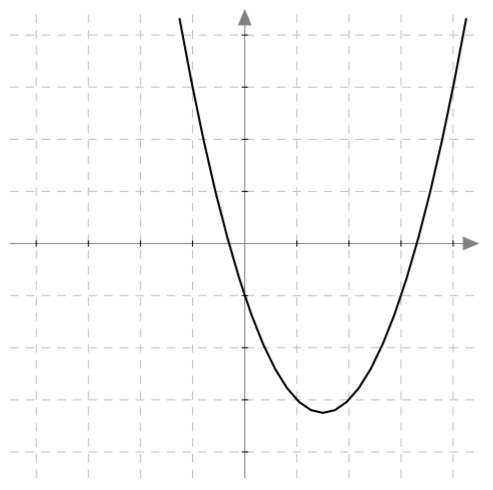
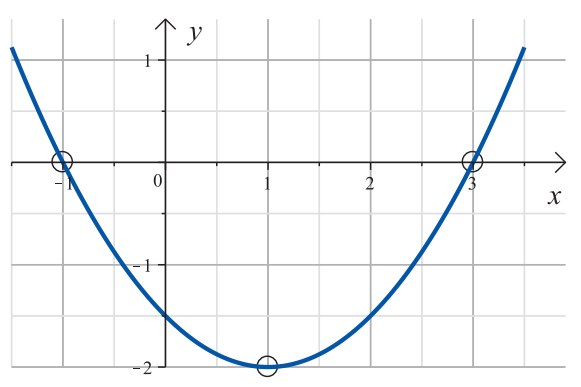
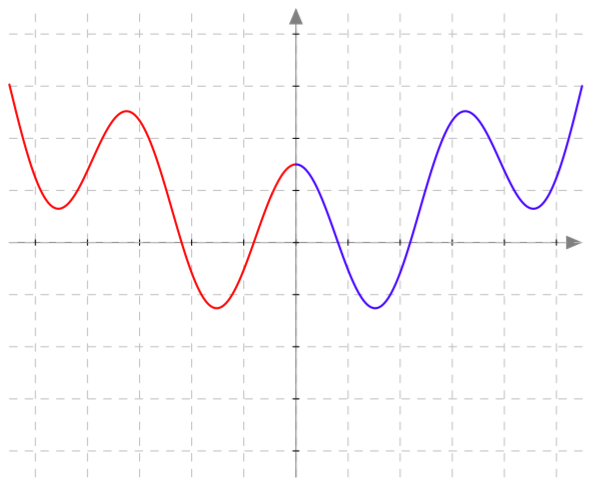
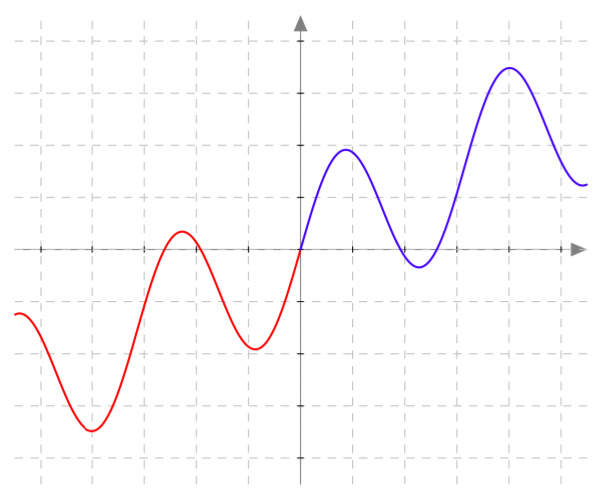
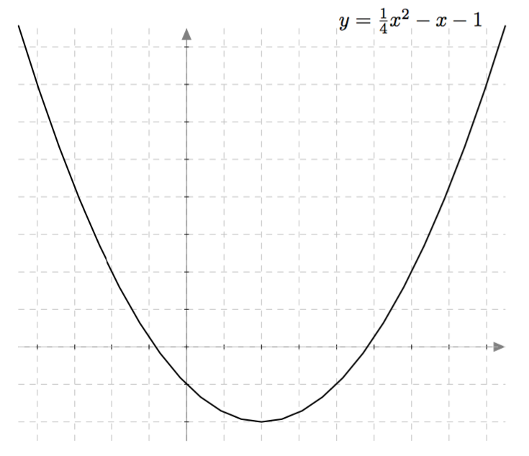
Alla on näkyvissä funktion $f(x) = \frac{1}{4}x^2-x-1$ kuvaaja. Päättele sen avulla seuraavien toisen asteen yhtälöiden ratkaisut tai ratkaisujen likiarvot:
- $\frac{1}{4}x^2-x-1 = 7$
- $\frac{1}{4}x^2-x-1 = 4$
- $\frac{1}{4}x^2-x-1 = 2$
- $\frac{1}{4}x^2-x-1 = 0$
- $\frac{1}{4}x^2-x-1 = -1$
- $\frac{1}{4}x^2-x-1 = -2$
- $\frac{1}{4}x^2-x-1 = -3$
- $x = -4 \ $ tai $\ x = 8$
- $x \approx -2{,}9 \ $ tai $\ x = 6{,}9$
- $x = -2 \ $ tai $\ x = 6$
- $x \approx -0{,}8 \ $ tai $\ x = 4{,}8$
- $x = 0 \ $ tai $\ x = 4$
- $x = 2$
- Ei ratkaisua.
MÄÄRITELMÄ: TOISEN ASTEEN YHTÄLÖ
Toisen asteen yhtälö tarkoittaa yhtälöä, joka voidaan esittää muodossa $$ax^2 + bx + c = 0,$$ missä $a \neq 0$.
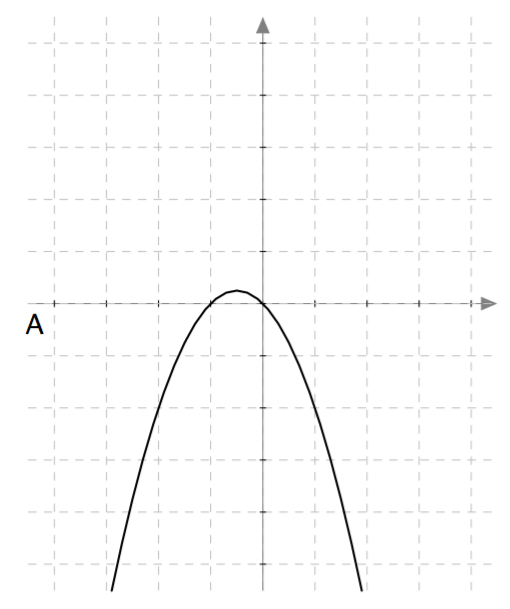
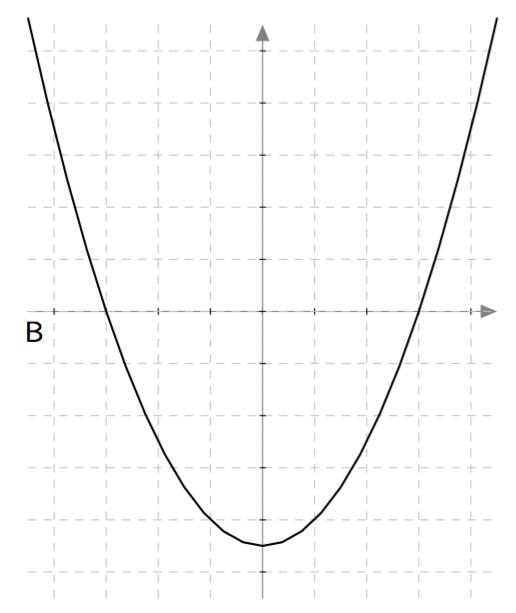
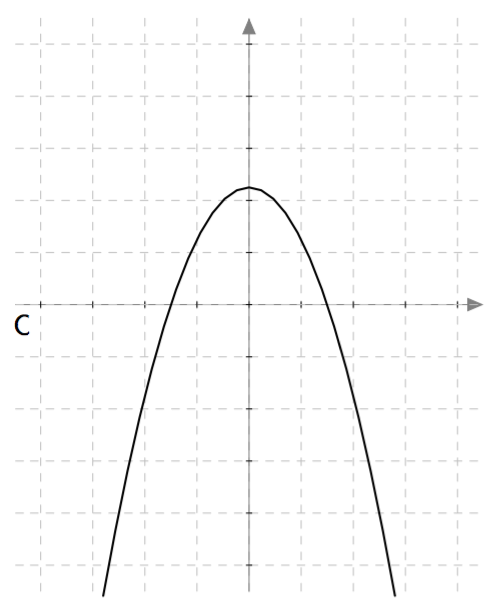
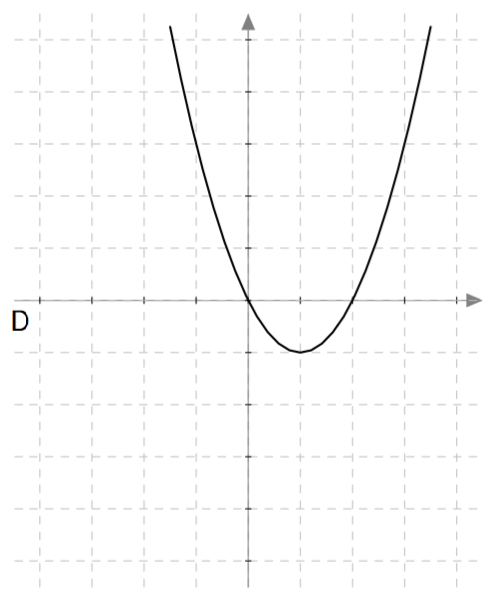
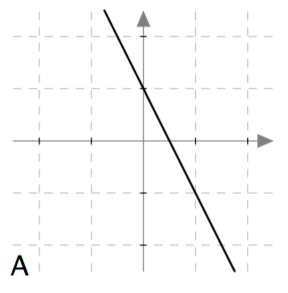
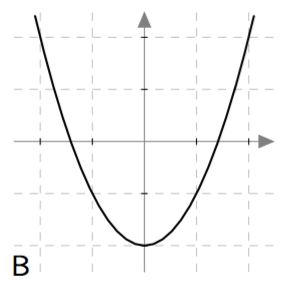
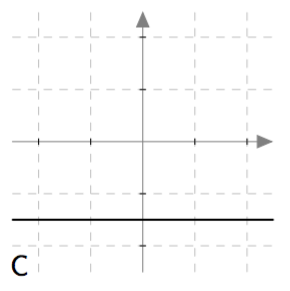
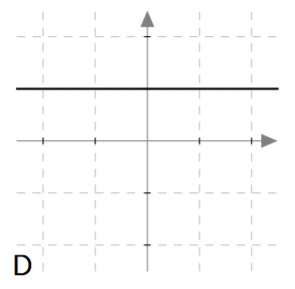
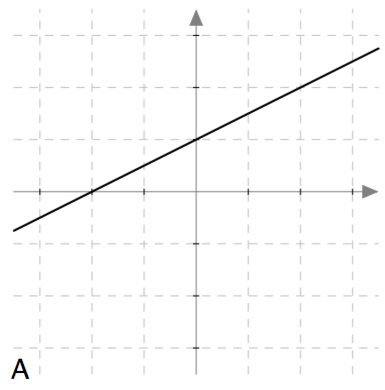
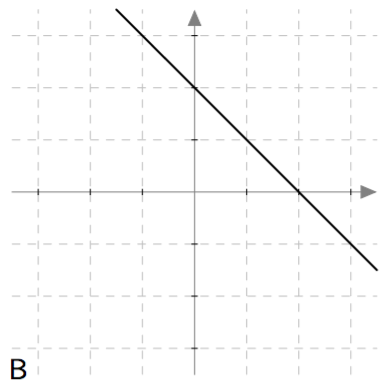
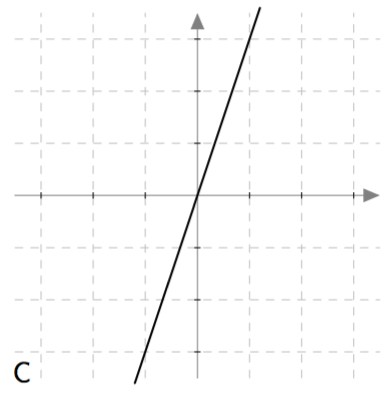
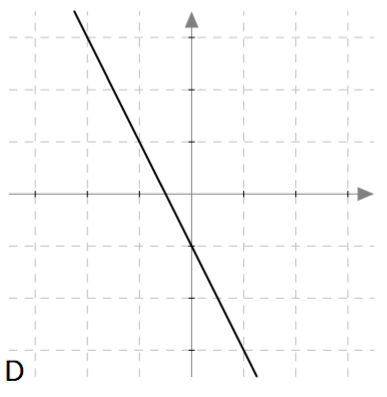
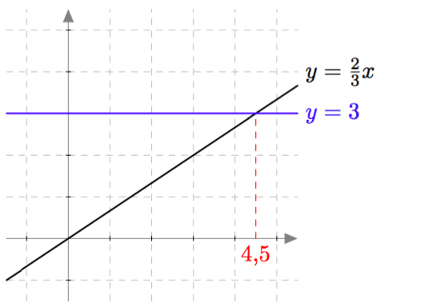
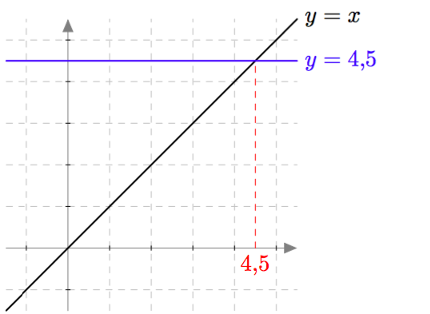
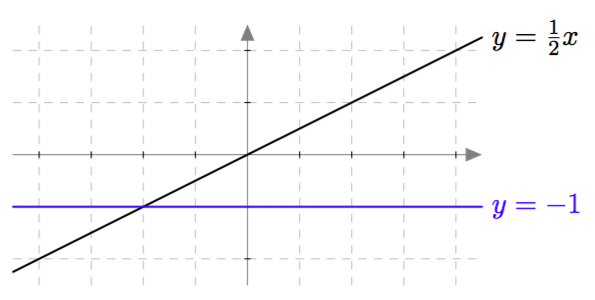
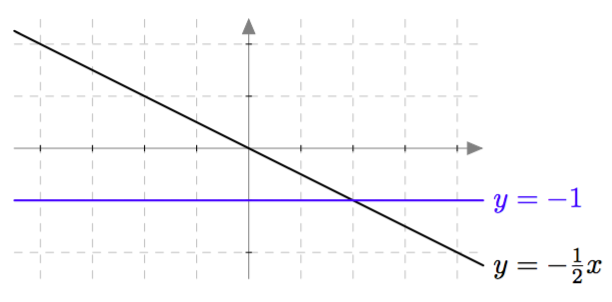
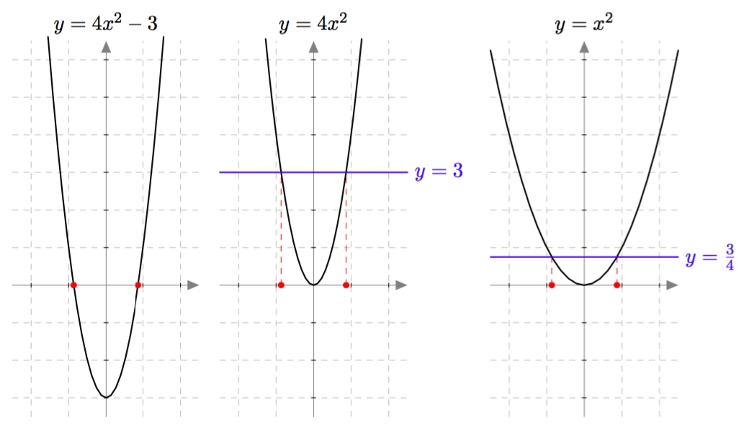
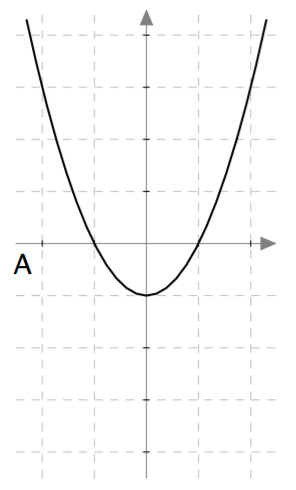
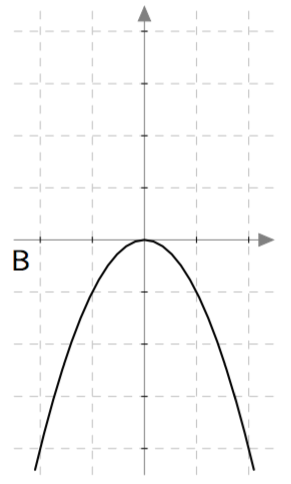
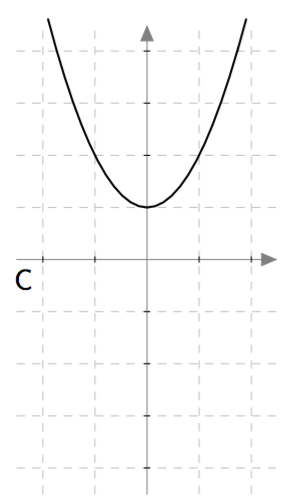
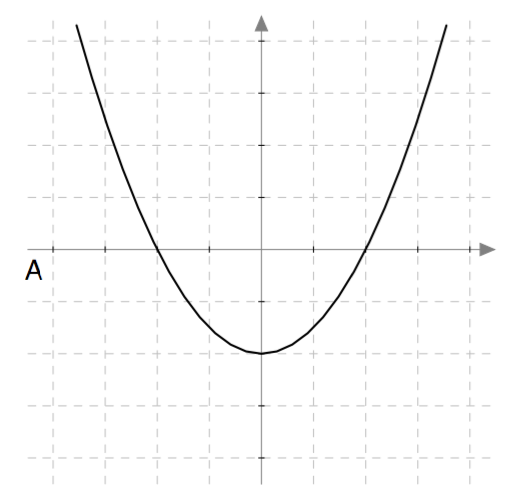
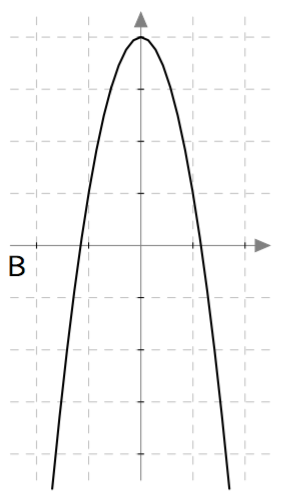
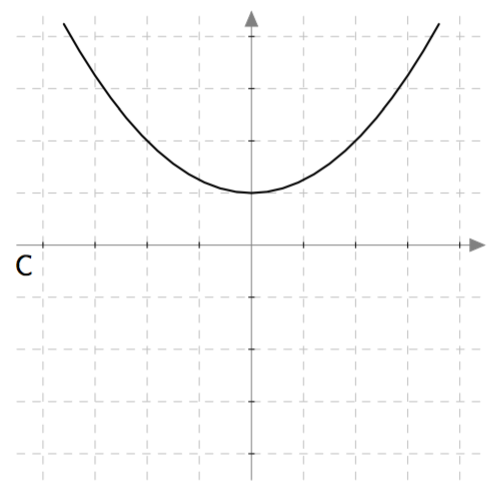
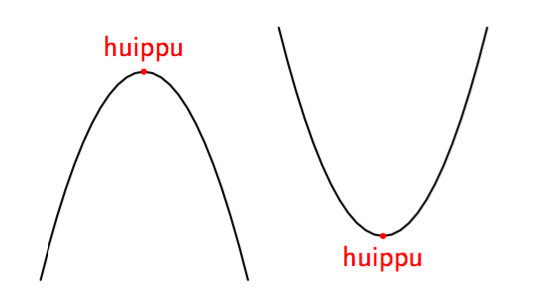
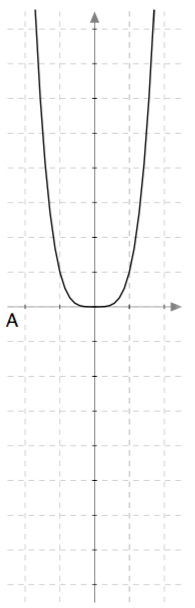
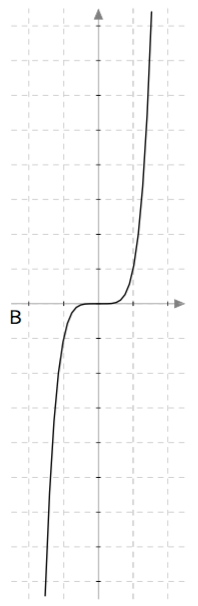
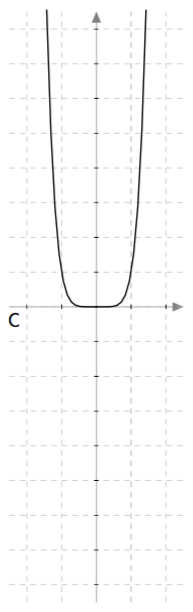
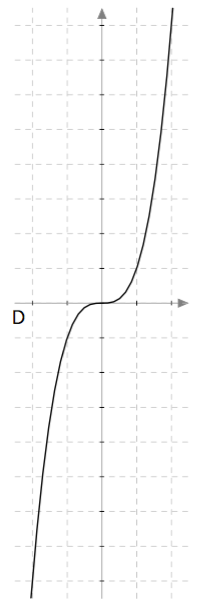
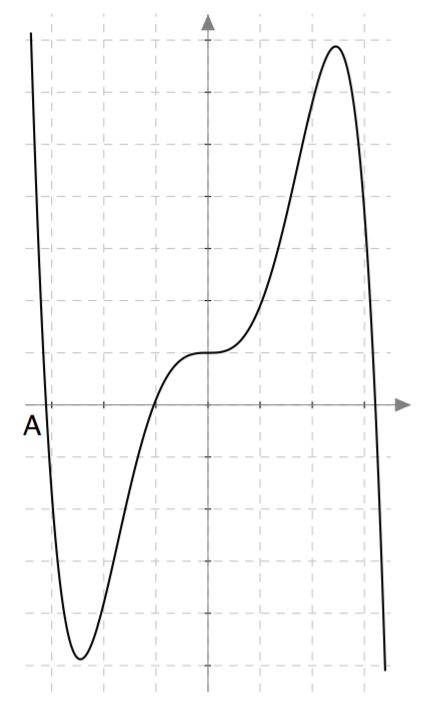
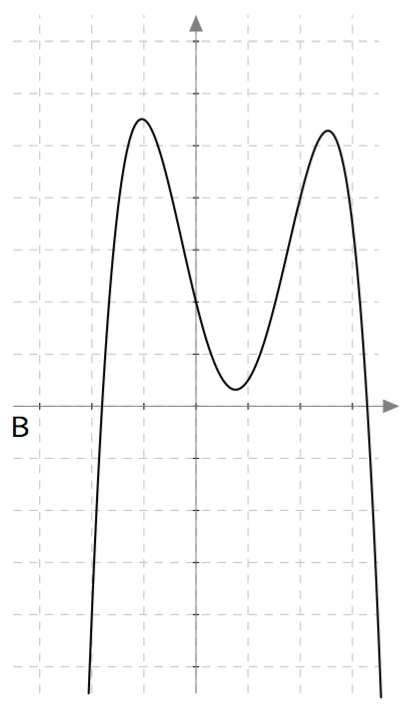
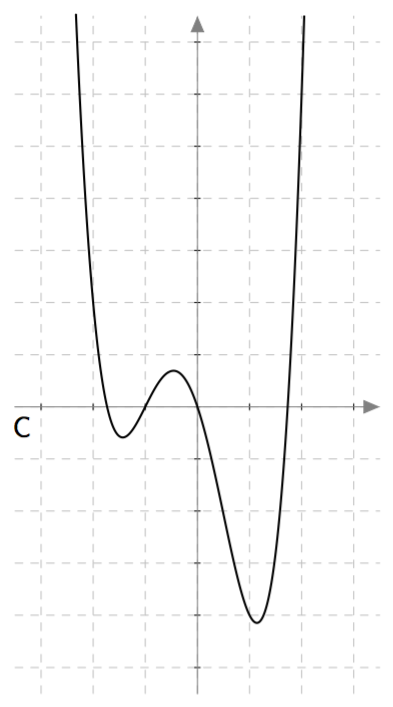
Yllä on näkyvissä toisen asteen polynomifunktioiden kuvaajia. Kopioi alla oleva taulukko vihkoosi ja täydennä se yhdistämällä oikea kuvaaja jokaiseen yhtälöön. Päättele lisäksi yhtälöiden ratkaisut kuvaajien avulla.
| Yhtälö | Funktion kuvaaja | Yhtälön ratkaisut |
| $\phantom{\dfrac{1}{1}}\phantom{-}x^2-2x = 0\,$ | | |
| $\phantom{\dfrac{1}{1}}-x^2-x = 0\,$ | | |
| $\phantom{\dfrac{1}{1}}\frac{1}{2}x^2- \frac{9}{2} = 0\,$ | | |
| $\phantom{\dfrac{1}{1}}-x^2 + \frac{9}{4} = 0\, $ | | |
Selitä omin sanoin, mitä voisi tämän tehtävän perusteella päätellä
- muotoa $ax^2 + c = 0$ olevan toisen asteen polynomiyhtälön ratkaisujen sijainnista $x$-akselilla
- muotoa $ax^2 + bx = 0$ olevan toisen asteen polynomiyhtälön ratkaisujen sijainnista $x$-akselilla.
| Yhtälö | Funktion kuvaaja | Yhtälön ratkaisut |
| $\phantom{\dfrac{1}{1}}\phantom{-}x^2-2x = 0\,$ | D | $2$ ja $0$ |
| $\phantom{\dfrac{1}{1}}-x^2-x = 0\,$ | A | $-1$ ja $0$ |
| $\phantom{\dfrac{1}{1}}\frac{1}{2}x^2- \frac{9}{2} = 0\,$ | B | $3$ ja $-3$ |
| $\phantom{\dfrac{1}{1}}-x^2 + \frac{9}{4} = 0\, $ | C | $\frac{3}{2}$ ja $-\frac{3}{2}$ |
- Ratkaisut sijaitsevat $x$-akselilla symmetrisesti origon molemmin puolin.
- Toinen ratkaisu on nolla ja toinen on $-\frac{b}{a}$.
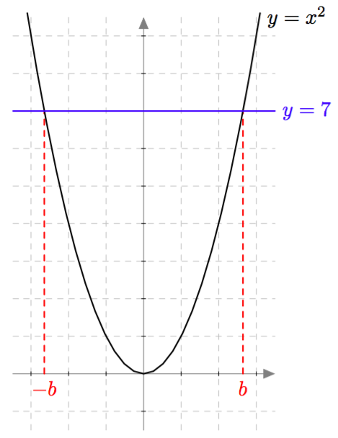
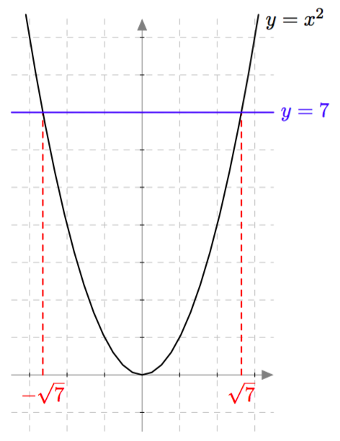
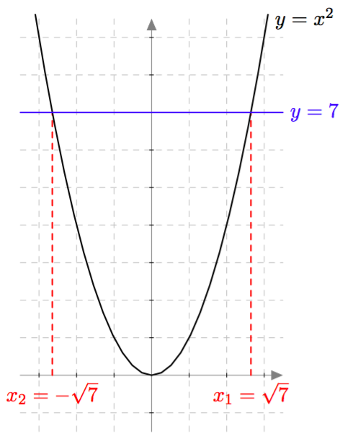
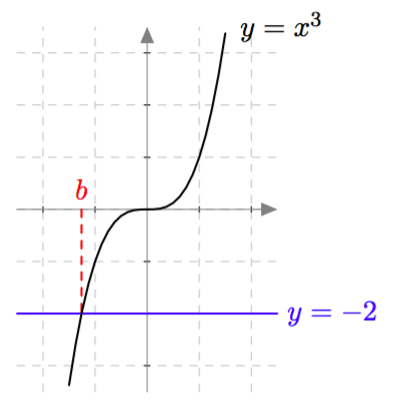
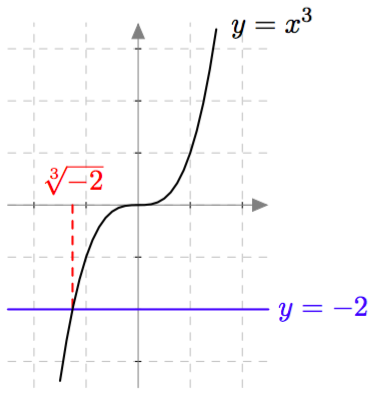
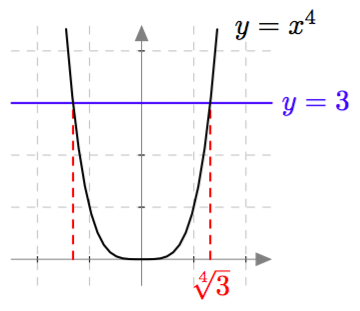
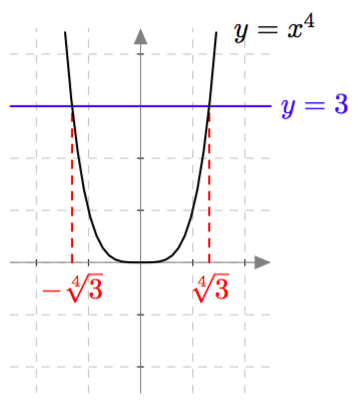
Muotoa $ax^2 + c = 0$ olevat toisen asteen polynomiyhtälöt saadaan muokattua toisen asteen potenssiyhtälöiksi. Esimerkiksi yhtälöä $3x^2 - 21 = 0$ voidaan muokata seuraavasti: \begin{align*} 3x^2 - 21 &= 0 &\quad &\mid + 21 \\ 3x^2 &= 21 &\quad &\mid \ : 3 \\ x^2 &= 7 \end{align*} Tiedetään, että tällä yhtälöllä on kaksi ratkaisua. Ensinnäkin $\sqrt{7}$ toteuttaa yhtälön $x^2 = 7$, sillä neliöjuuren määritelmän mukaan $\sqrt{7}$ tarkoittaa sitä epänegatiivista lukua, jonka toinen potenssi on $7$. Lisäksi myös $-\sqrt{7}$ toteuttaa yhtälön $x^2 = 7$:
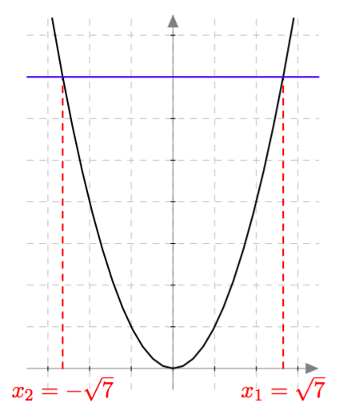
Ratkaise seuraavat toisen asteen polynomiyhtälöt:
- $2x^2 = 50$
- $7x^2 - 14 = 0$
- $3x^2 - 16 = 2x^2 + 20$
- $x = -5 \ $ tai $\ x = 5$
- $x = \sqrt{2} \ $ tai $\ x = -\sqrt{2}$
- $x = 6 \ $ tai $\ x = -6$
Edellisessä kappaleessa tutustuttiin tulon nollasääntöön, jonka mukaan reaalilukujen tulo on nolla, jos ja vain jos ainakin yksi tulon tekijöistä on nolla. Sen avulla saadaan ratkaistua muotoa $ax^2 + bx = 0$ olevat toisen asteen polynomiyhtälöt. Tällaisten yhtälöiden vasemmalta puolelta voidaan erottaa yhteinen tekijä $x$, minkä jälkeen yhtälön vasen puoli voidaan kirjoittaa tulona.
Esimerkiksi yhtälö $$x^2-3x = 0$$ voidaan kirjoittaa muodossa $$x(x-3) = 0.$$ Tulon nollasäännön mukaan tämä yhtälö toteutuu, jos ja vain jos $$x = 0 \quad \text{ tai } \quad x - 3 = 0$$ eli $$x = 0 \quad \text{ tai } \quad x = 3.$$
Ratkaise seuraavat toisen asteen polynomiyhtälöt tulon nollasäännön avulla:
- $x^2-4x = 0$
- $3x^2+15x = 0$
- $2x^2 - x = 0$
- $x = 0 \ $ tai $\ x = 4$
- $x = 0 \ $ tai $\ x = -5$
- $x = 0 \ $ tai $\ x = \dfrac{1}{2}$
Jotkin toisen asteen yhtälöt saadaan kirjoitettua toiseen muotoon aiemmin opiskeltuja summan ja erotuksen neliön kaavoja käyttäen. Esimerkiksi käyttämällä summan neliön kaavaa $$\textcolor{red}{a}^2 + 2\textcolor{red}{a}\textcolor{blue}{b} + \textcolor{blue}{b}^2 = (\textcolor{red}{a} + \textcolor{blue}{b})^2$$ yhtälö $$\textcolor{red}{x}^2 + 2\textcolor{red}{x} + \textcolor{blue}{1} = 0$$ eli yhtälö $$\textcolor{red}{x}^2 + 2\textcolor{red}{x} \cdot \textcolor{blue}{1} + \textcolor{blue}{1}^2 = 0$$ saadaan kirjoitettua muodossa $$(\textcolor{red}{x}+\textcolor{blue}{1})^2 = 0.$$ Tämä yhtälö voidaan nyt ratkaista samaan tapaan kuin toisen asteen potenssiyhtälö. Luvun $x+1$ toinen potenssi on nolla, jos ja vain jos kantaluku $x+1$ on nolla, eli $$x + 1 = 0.$$ Kun tämän yhtälön molemmilta puolilta vähennetään luku $1$, saadaan ratkaisu $$x = -1.$$
Ratkaise seuraavat toisen asteen polynomiyhtälöt hyödyntämällä summan tai erotuksen neliötä samaan tapaan kuin edellä:
- $x^2 + 10x + 25 = 0$
- $x^2 - 6x + 9 = 0$
- $4x^2 + 4x + 1 = 0$
- $x = -5$
- $x = 3$
- $x = -\dfrac{1}{2}$
Edellisen tehtävän ideaa voidaan soveltaa myös tilanteissa, joissa yhtälön oikealla puolella ei olekaan nolla. Tarkastellaan esimerkiksi yhtälöä $$25x^2 - 40x + 16 = 100.$$ Käyttämällä erotuksen neliön kaavaa $$\textcolor{red}{a}^2 - 2\textcolor{red}{a}\textcolor{blue}{b} + \textcolor{blue}{b}^2 = (\textcolor{red}{a} - \textcolor{blue}{b})^2$$ voidaan tarkasteltu yhtälö $$(\textcolor{red}{5x})^2 - 2 \cdot \textcolor{red}{5x} \cdot \textcolor{blue}{4} + \textcolor{blue}{4}^2 = 100$$ kirjoittaa muodossa $$(\textcolor{red}{5x}-\textcolor{blue}{4})^2 = 100.$$ Tämä yhtälö voidaan jälleen ratkaista samaan tapaan kuin toisen asteen potenssiyhtälö: \begin{align*} (5x-4)^2 &= 100 \\[1mm] 5x - 4 = 10 \quad &\text{ tai } \quad 5x - 4 = -10 \\[1mm] 5x = 14 \quad &\text{ tai } \quad \quad \ \ 5x = -6 \\[1mm] \ \ x = \frac{14}{5} \quad &\text{ tai } \quad \quad \quad x = -\frac{6}{5} \end{align*}
Ratkaise seuraavat toisen asteen polynomiyhtälöt. Hyödynnä tarvittaessa summan tai erotuksen neliöiden kaavoja.
- $(x-2)^2 = 16$
- $9x^2 + 6x + 1 = 4$
- $4x^2 - 12x + 9 = 49$
- $x = -2 \ $ tai $\ x = 6$
- $x = -1 \ $ tai $\ x = \dfrac{1}{3}$
- $x = -2 \ $ tai $\ x = 5$
Voidaan osoittaa, että mikä tahansa toisen asteen polynomiyhtälö voidaan muuttaa sellaiseen muotoon, että se voidaan ratkaista edellisten tehtävien ideoita hyödyntäen. Tätä menetelmää sanotaan neliöksi täydentämiseksi.
Tarkastellaan esimerkiksi yhtälöä $$x^2-x-6 = 0.$$ Se voidaan kirjoittaa myös muodossa $$x^2 - 2\cdot \frac{1}{2}x = 6,$$ sillä $2\cdot \frac{1}{2} = 1$. Kun tämän yhtälön vasenta puolta verrataan erotuksen neliön kaavaan $$\textcolor{red}{a}^2 - 2\textcolor{red}{a}\textcolor{blue}{b} + \textcolor{blue}{b}^2 = (\textcolor{red}{a} - \textcolor{blue}{b})^2,$$ huomataan, että $a = x$ ja $b = \frac{1}{2}$: $$\textcolor{red}{x}^2 - 2 \cdot \textcolor{red}{x} \cdot \textcolor{blue}{\frac{1}{2}} = 6.$$ Yhtälön vasemmalta puolelta kuitenkin puuttuu termiä $\textcolor{blue}{b}^2$ vastaava termi. Tämä ongelma ratkeaa, kun yhtälön molemmille puolille lisätään $\left(\frac{1}{2}\right)^2$: $$\textcolor{red}{x}^2 - 2 \cdot \textcolor{red}{x} \cdot \textcolor{blue}{\frac{1}{2}} + \left(\textcolor{blue}{\frac{1}{2}}\right)^2 = 6 + \left(\frac{1}{2}\right)^2.$$ Nyt yhtälö voidaan erotuksen neliön kaavan avulla kirjoittaa muodossa $$\left(\textcolor{red}{x}-\textcolor{blue}{\frac{1}{2}}\right)^2 = 6 + \frac{1}{4}$$ eli $$\left(x-\frac{1}{2}\right)^2 = \frac{25}{4}.$$ Tämä yhtälö toteutuu, jos ja vain jos \begin{align*} x-\frac{1}{2} = \sqrt{\frac{25}{4}} \quad &\text{ tai } \quad x-\frac{1}{2} = -\sqrt{\frac{25}{4}} \\[1mm] x-\frac{1}{2} = \frac{5}{2} \quad &\text{ tai } \quad x-\frac{1}{2} = -\frac{5}{2} \\[1mm] \ \ x = \frac{6}{2} \quad &\text{ tai } \quad \quad \quad x = -\frac{4}{2} \\[1mm] \ \ x = 3 \quad &\text{ tai } \quad \quad \quad x = -2 \end{align*}
Ratkaise seuraavat toisen asteen polynomiyhtälöt. Täydennä yhtälön vasen puoli ensin summan tai erotuksen neliöksi samaan tapaan kuin edellä.
- $x^2 - 4x + 3 = 0$
- $x^2 + 10x - 24 = 0$
- Yhtälö $(x-2)^2 = 1$, ratkaisut $x = 1 \ $ tai $\ x = 3$
- Yhtälö $(x+5)^2 = 49$, ratkaisut $x = -12 \ $ tai $\ x = 2$
Myös seuraavan teoreeman menetelmä toisen asteen polynomiyhtälön ratkaisemiseen perustustuu neliöksi täydentämiseen. Lue teoreeman perustelu huolellisesti ja mieti jokaisen virkkeen jälkeen, mitä järkeä selityksessä on. Jos jokin kohta tuntuu hämärältä, keskustele siitä kaverin tai opettajan kanssa.
TEOREEMA
Toisen asteen yhtälön $ax^2 + bx + c = 0$ ratkaisut saadaan kaavalla $$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}.$$ Jos neliöjuurimerkin alle tuleva luku on negatiivinen eli $b^2-4ac < 0$, ei yhtälöllä ole ratkaisuja.
Perustelu: Ideana on täydentää yhtälön vasen puoli summan neliöksi. Jotta se onnistuisi helpommin, kerrotaan aluksi yhtälön $ax^2 + bx + c = 0$ molemmat puolet luvulla $4a$ (huomaa, että $a \neq 0$, joten myös $4a \neq 0$). Näin päädytään yhtälöön $$4a^2x^2 + 4abx + 4ac = 0.$$ Vähennetään yhtälön molemmilta puolilta $4ac$, jolloin saadaan yhtälö $$(\textcolor{red}{2ax})^2 + 2\cdot \textcolor{red}{2ax}\textcolor{blue}{b} = -4ac.$$ Lisätään tämän yhtälön molemmille puolille neliöksi täydentämiseen tarvittava termi $b^2$, jolloin saadaan yhtälö $$(\textcolor{red}{2ax})^2 + 2\cdot \textcolor{red}{2ax}\textcolor{blue}{b} + \textcolor{blue}{b}^2= -4ac + b^2.$$ Summan neliön kaavan nojalla yhtälö voidaan nyt kirjoittaa muodossa $$(\textcolor{red}{2ax} + \textcolor{blue}{b})^2 = b^2-4ac.$$ Jos yhtälön oikea puoli on negatiivinen eli $b^2-4ac < 0$, ei yhtälöllä ole ratkaisuja, sillä yhtälön vasen puoli on toisena potenssina aina epänegatiivinen.
Jos yhtälön oikea puoli on epänegatiivinen eli $b^2-4ac \geq 0$, yhtälö toteutuu, jos ja vain jos \begin{align*} 2ax+b &= \pm\sqrt{b^2-4ac} \\[1mm] 2ax &= -b\pm\sqrt{b^2-4ac} \\[1mm] x &= \frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{align*}
Teoreeman 5 mukaan toisen asteen yhtälöllä $ax^2 + bx + c = 0$ voi olla kaksi ratkaisua, yksi ratkaisu tai ei yhtään ratkaisua. Jos neliöjuurimerkin alle tuleva luku on positiivinen eli $b^2-4ac > 0$, saadaan ratkaisuja kaksi: $$x_1 = \frac{-b+\sqrt{b^2-4ac}}{2a}$$ ja $$x_2 = \frac{-b-\sqrt{b^2-4ac}}{2a}.$$
Esimerkiksi yhtälön $x(2x-3)-3x(1-x) = -1$ ratkaisut saadaan selville, kun yhtälö ensin sievennetään perusmuotoon $ax^2 + bx + c = 0$: \begin{align*} x(2x-3)-3x(1-x) &= -1 \\ 2x^2-3x-3x+3x^2 &= -1 \\ 5x^2-6x + 1 &= 0\\ \end{align*} Tästä nähdään, että $a = 5$, $b = -6$ ja $c = 1$. Tarkasteltu yhtälö siis toteutuu, jos ja vain jos \begin{align*} x &= \frac{-(-6) \pm \sqrt{(-6)^2-4\cdot 5 \cdot 1}}{2\cdot 5} \\ &= \frac{6 \pm \sqrt{16}}{10} \\ &= \frac{6 \pm 4}{10} \end{align*} eli $x = 1$ tai $x = \dfrac{1}{5}$.
Ratkaise seuraavat toisen asteen polynomiyhtälöt teoreemassa 5 esitetyn ratkaisukaavan avulla. Muuta yhtälö ensin perusmuotoon $ax^2+bx+c = 0$ ja tunnista, mitkä luvut vastaavat kirjaimia $a$, $b$ ja $c$. Huomioi myös etumerkit.
- $3x^2 - 7x + 4 = 0$
- $x^2 + 2x - 9 = 3x - 7$
- $x^2 = 3x$
- $(-3x-1)(x-2) = 4$
- $x = \dfrac{4}{3} \ $ tai $\ x = 1$
- $x = -1 \ $ tai $\ x = 2$
- $x = 0 \ $ tai $\ x = 3$
- $x = \dfrac{2}{3} \ $ tai $\ x = 1$
Seuraavissa tehtävissä harjoitellaan tunnistamaan erilaisille toisen asteen yhtälöille sopivat ratkaisutavat.
Edellisissä tehtävissä on harjoiteltu seuraavia ratkaisutapoja
- ratkaisu potenssiyhtälönä ($x^2 = d$)
- ratkaisu tulon nollasäännön avulla
- ratkaisu summan tai neliön erotuksen kaavan avulla
- ratkaisu ratkaisukaavan avulla
Kopioi alla oleva taulukko vihkoosi ja täydennä siihen, mikä ratkaisutapa sopii parhaiten kyseiselle yhtälölle. Ratkaise yhtälöt sen jälkeen. Voit tarkistaa tulokset laskimella.
| Yhtälö | Ratkaisutapa | Yhtälön ratkaisut |
| $(x-5)(1-3x) = 0$ | | |
| $2x^2+x = 3$ | | |
| $4x^2-4x+1 = 0$ | | |
| $(3x-1)(x+2) = 6$ | | |
| $3x^2-12 = 0$ | | |
| $5x^2-2x = 0$ | | |
Ratkaise seuraavat yhtälöt niin monella erilaisella tavalla kuin mahdollista. Ainakin kaksi ratkaisutapaa on mahdollista keksiä.
- $(5x+4)(2x-1) = 0$
- $(2x-3)^2 - 9 = 0$
- Tulon nollasäännön tai ratkaisukaavan avulla; $x = -\dfrac{4}{5} \ $ tai $\ x = \dfrac{1}{2}$
- Päättelemällä $2x - 3 = 3$ tai $2x - 3 = -3$, josta ratkaisut $x = 3 \ $ tai $\ x = 0$. Toinen vaihtoehto on käyttää ratkaisukaavaa.
Toisen asteen yhtälön ratkaisujen lukumäärää voidaan tutkia niin sanotun diskriminantin avulla:
MÄÄRITELMÄ: DISKRIMINANTTI
Toisen asteen yhtälön $ax^2 + bx + c = 0$ diskriminantti $D$ tarkoittaa ratkaisukaavassa neliöjuurimerkin alle tulevaa lukua $b^2-4ac$: $$D = b^2-4ac.$$
Piirrä laskimellasi seuraavien polynomifunktioiden $f(x) = ax^2 + bx + c$ kuvaajat. Päättele kuvaajan avulla, mitkä ovat funktion $f$ nollakohdat eli vastaavan toisen asteen yhtälön $ax^2 + bx + c = 0$ ratkaisut. Laske myös tämän yhtälön diskriminantti. Miten voisit suoraan diskriminantin avulla päätellä ratkaisujen lukumäärän?
- $f(x) = x^2-6x+9$
- $f(x) = -x^2-2x$
- $f(x) = 2x^2+x-1$
- $f(x) = x^2-2x+2$
- $D = 0$ ja yhtälöllä on tasan yksi ratkaisu, $x = 3$.
- $D = 4$ ja yhtälöllä on kaksi ratkaisua, $x_1 = 0$ ja $x_2 = -2$.
- $D = 9$ ja yhtälöllä on kaksi ratkaisua, $x_1 = -1$ ja $x_2 = \dfrac{1}{2}$.
- $D = -4$ eikä yhtälöllä ole yhtään ratkaisua.
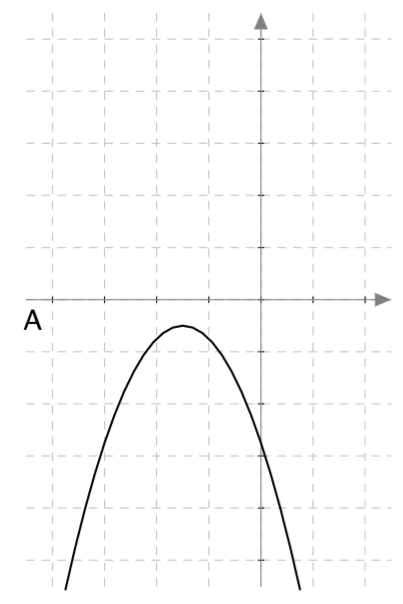
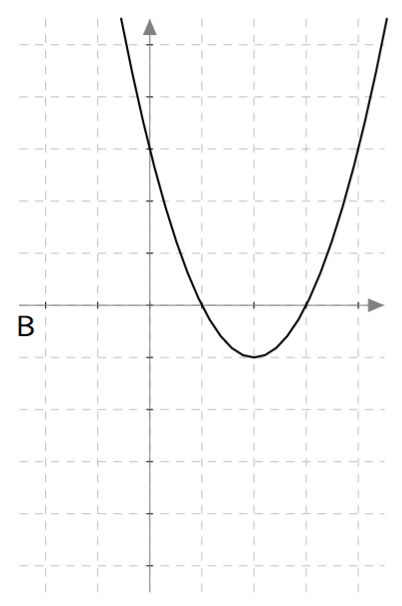
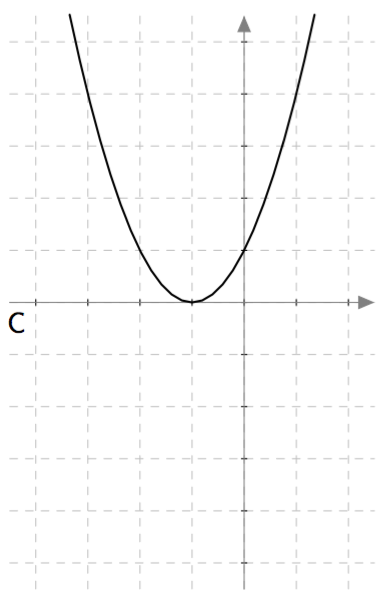
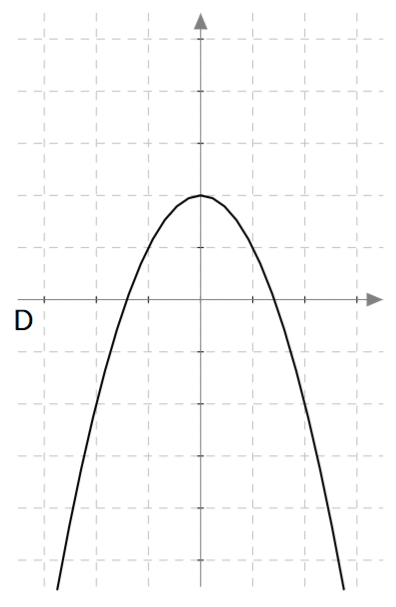
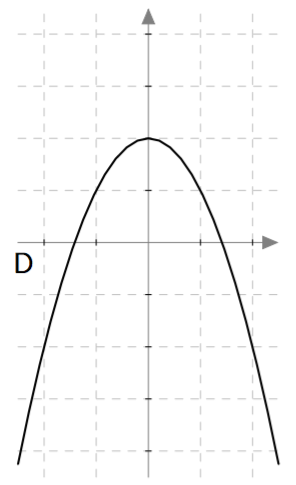
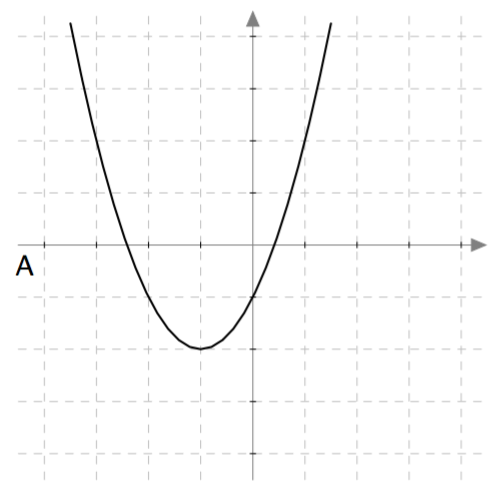
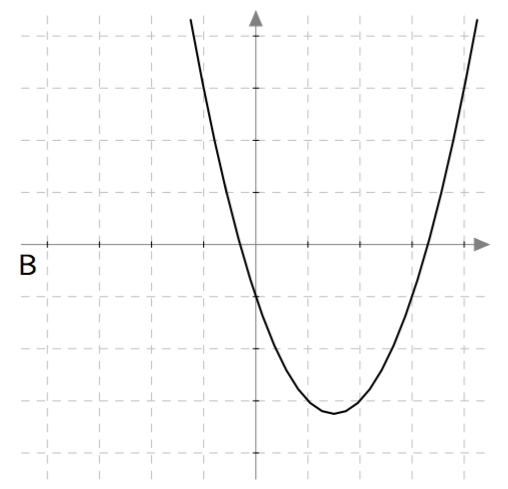
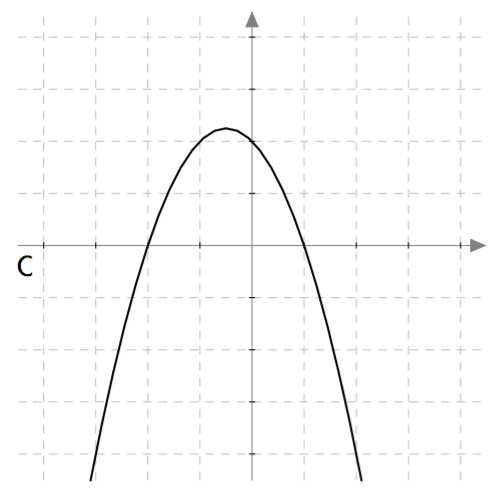
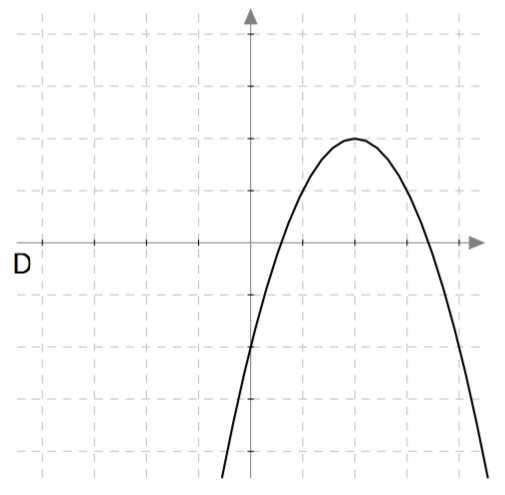
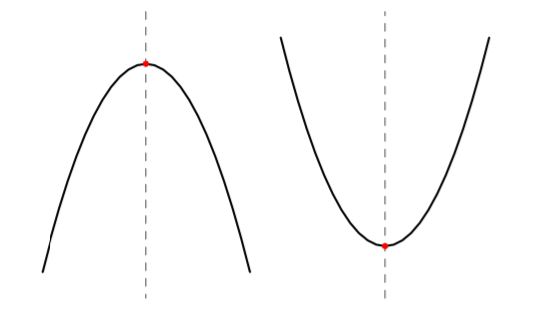
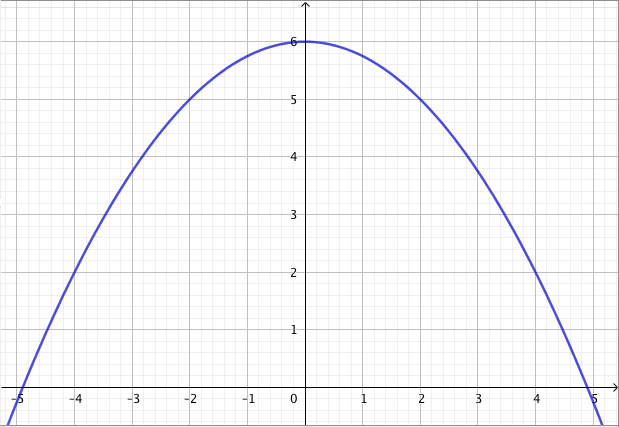
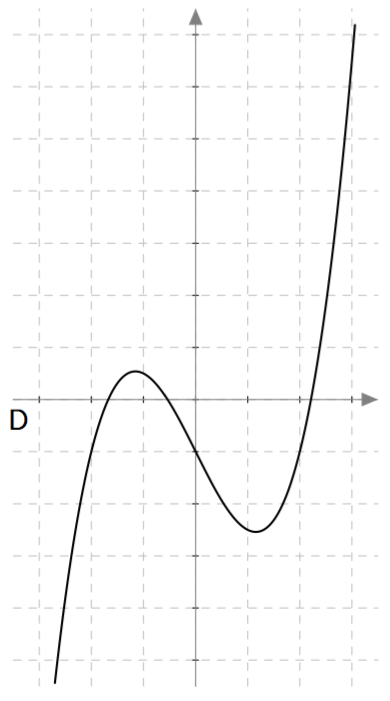
Yllä on näkyvissä toisen asteen polynomifunktioiden $f(x) = ax^2 + bx + c$ kuvaajia. Päättele kuvaajan avulla funktion nollakohtien lukumäärä eli yhtälön $ax^2 + bx + c = 0$ ratkaisujen lukumäärä. Päättele myös, onko yhtälön diskriminantti positiivinen, negatiivinen vai nolla, ja täydennä nämä tiedot taulukkoon.
| Kuvaaja | Nollakohtien määrä | Diskriminantti |
| A | | |
| B | | |
| C | | |
| D | | |
| Kuvaaja | Nollakohtien määrä | Diskriminantti |
| A | 0 | Negatiivinen |
| B | 2 | Positiivinen |
| C | 1 | Nolla |
| D | 2 | Positiivinen |
Edellisten tehtävien havainnot voidaan koota seuraavaksi teoreemaksi:
TEOREEMA
Toisen asteen yhtälön $ax^2 + bx + c = 0$ ratkaisujen lukumäärä voidaan päätellä diskriminantin $D = b^2-4ac$ avulla seuraavasti:
- jos $D > 0$, yhtälöllä on kaksi ratkaisua
- jos $D = 0$, yhtälöllä on yksi ratkaisu
- jos $D < 0$, yhtälöllä ei ole yhtään ratkaisua.
Perustelu: Jos yhtälön $ax^2 + bx + c = 0$ diskriminantti on negatiivinen eli $D < 0$, niin teoreeman 5 mukaan yhtälöllä $ax^2 + bx + c = 0$ ei ole yhtään ratkaisua. Jos diskriminantti on epänegatiivinen eli $D \geq 0$, ratkaisut saadaan kaavalla $$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$$ eli $$x = \frac{-b \pm \sqrt{D}}{2a}.$$ Jos $D > 0$, on myös $\sqrt{D} > 0$, ja ratkaisuja saadaan kaksi. Jos $D = 0$, ratkaisuja on yksi: $$x = \frac{-b}{2a}.$$
Jos toisen asteen yhtälöllä $ax^2 + bx + c = 0$ on kaksi ratkaisua eli juurta, ne ovat teoreeman 5 mukaan $$x_1 = \frac{-b+\sqrt{b^2-4ac}}{2a}$$ ja $$x_2 = \frac{-b-\sqrt{b^2-4ac}}{2a}.$$ Merkitään $D = b^2-4ac$. Tällöin ratkaisut voidaan kirjoittaa $$x_1 = \frac{-b+\sqrt{D}}{2a}$$ ja $$x_2 = \frac{-b-\sqrt{D}}{2a}.$$
- Sievennä juurten summa $x_1 + x_2$ mahdollisimman pitkälle.
- Sievennä juurten tulo $x_1x_2$ mahdollisimman pitkälle.
Muista, että $D = b^2-4ac$.
- $$x_1 + x_2 = \frac{-2b}{2a} = -\frac{b}{a}$$
- $$ x_1x_2 = \frac{b^2 - D}{4a^2} = \frac{c}{a} $$
Edellisen tehtävän tuloksena saadaan seuraava teoreema:
TEOREEMA
Jos luvut $x_1$ ja $x_2$ ovat toisen asteen yhtälön $ax^2 + bx + c = 0$ ratkaisut eli juuret, niiden summa on $$x_1 + x_2 = -\frac{b}{a}$$ ja tulo on $$x_1x_2 = \frac{c}{a}.$$ Tämä pätee siinäkin tapauksessa, että $x_1 = x_2$, eli yhtälöllä on vain yksi ratkaisu.
Perustelu tehtävässä 3.26.
Aiemmin tässä kappaleessa olet ratkaissut toisen asteen yhtälöitä tulon nollasäännön avulla. Tällöin toisen asteen polynomi jaetaan tekijöihin erottamalla yhteinen tekijä: esimerkiksi yhtälö $2x^2 - 5x = 0$ voidaan ratkaista kirjoittamalla se muodossa $$x(2x-5) = 0.$$ Joitakin toisen asteen yhtälöitä olet ratkaissut summan ja erotuksen neliöiden kaavoja käyttäen. Tällöinkin polynomi tullaan jakaneeksi tekijöihin: esimerkiksi yhtälö $4x^2+20x + 25 = 0$ voidaan ratkaista kirjoittamalla se muodossa $$(2x+5)^2 = 0.$$ Seuraavaksi tutkitaan käänteistä tilannetta: Miten toisen asteen polynomi saadaan jaettua tekijöihin, jos vastaavan toisen asteen yhtälön ratkaisut tunnetaan?
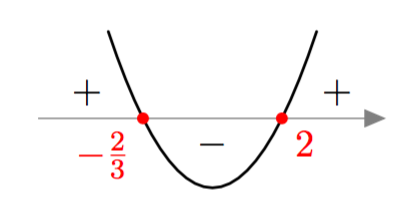
Yhtälön $12x^2-x-6 = 0$ ratkaisut ovat $x_1 = \dfrac{3}{4}$ ja $x_2 = -\dfrac{2}{3}$.
- Tarkista, että luvut $x_1$ ja $x_2$ todella ovat yhtälön $12x^2-x-6 = 0$ ratkaisut. Keksitkö kaksi erilaista tapaa tarkistuksen tekemiseen?
- Tarkista, ovatko juurten $x_1$ ja $x_2$ summa ja tulo teoreeman 6 mukaiset.
- Sijoita luvut $x_1$ ja $x_2$ lausekkeeseen $12(x-x_1)(x-x_2)$ ja sievennä se mahdollisimman pitkälle. Vertaa tulosta alkuperäiseen yhtälöön. Mitä huomaat?
- Luvut voi sijoittaa yhtälön vasemman puolen lausekkeeseen $12x^2 - x - 6$ ja tutkia, tuleeko tulokseksi nolla.
Toinen mahdollisuus on ratkaista yhtälö itse uudelleen.
Tutkitaan tilannetta, jossa toisen asteen yhtälöllä $ax^2 + bx + c = 0$ on kaksi ratkaisua tai yksi ratkaisu. Merkitään ratkaisuja $x_1$ ja $x_2$. Jos ratkaisuja on vain yksi, merkitään sitä sekä symbolilla $x_1$ että $x_2$. Tehtävänä on osoittaa, että $a(x-x_1)(x-x_2) = ax^2 + bx + c$.
- Kerro sulut auki lausekkeesta $a(x-x_1)(x-x_2)$ ja sievennä mahdollisimman pitkälle.
- Jatka sieventämistä hyödyntämällä teoreemaa 7, jonka mukaan juurten summa on $$x_1 + x_2 = -\frac{b}{a}$$ ja tulo on $$x_1x_2 = \frac{c}{a}.$$
- Lauseke sievenee muotoon $$ ax^2 - a(x_1+x_2)x + ax_1x_2 $$
- Lauseke sievenee edelleen muotoon $$ ax^2 + bx + c $$
Edellisessä tehtävässä toisen asteen polynomi $ax^2 + bx + c$ saatiin kirjoitettua tulomuodossa $$ax^2 + bx + c = a(x-x_1)(x-x_2)$$ eli jaettua ensimmäisen asteen tekijöihin $(x-x_1)$ ja $(x-x_2)$, missä $x_1$ ja $x_2$ ovat yhtälön $ax^2 + bx + c = 0$ ratkaisut. Tämä tulos on osa seuraavaa teoreemaa:
TEOREEMA
Toisen asteen polynomi $ax^2 + bx + c$ voidaan jakaa ensimmäisen asteen tekijöihin seuraavasti: jos yhtälöllä $ax^2 + bx + c = 0$
- on kaksi ratkaisua $x_1$ ja $x_2$, niin $$ax^2 + bx + c = a(x-x_1)(x-x_2)$$
- on yksi ratkaisu $x_1$, niin $$ax^2 + bx + c = a(x-x_1)^2$$
- ei ole yhtään ratkaisua, niin polynomilla $ax^2 + bx + c$ ei ole yhtään ensimmäisen asteen tekijää.
Perustelu: Kaksi ensimmäistä tapausta on käsitelty edellisessä tehtävässä. Tutkitaan vielä tapaus, jossa yhtälöllä $ax^2 + bx + c = 0$ ei ole yhtään ratkaisua. Jos tässä tilanteessa polynomilla $ax^2 + bx + c$ olisi jokin ensimmäisen asteen tekijä $sx+t$, polynomi $ax^2 + bx + c$ voitaisiin kirjoittaa tulona: $$ax^2 + bx + c = (sx+t)(\ldots)$$ Tällöin tulon nollasäännön nojalla yhtälön $$ax^2 + bx + c = 0$$ eli yhtälön $$(sx+t)(\ldots) = 0$$ yksi ratkaisu saataisiin yhtälöstä $sx + t = 0$. Yhtälöllä $ax^2 + bx + c = 0$ olisi siis ratkaisu $$x = -\dfrac{t}{s}.$$ Tämä on kuitenkin mahdotonta, koska tarkasteltiin tapausta, jossa yhtälöllä $ax^2 + bx + c = 0$ ei ole yhtään ratkaisua. Siis polynomilla $ax^2 + bx + c$ ei ole yhtään ensimmäisen asteen tekijää.
Teoreeman 8 avulla toisen asteen polynomi saadaan jaettua tekijöihin etsimällä ensin polynomin nollakohdat. Esimerkiksi jos polynomi $10x^2 + x - 3$ halutaan jakaa tekijöihin, ratkaistaan ensin yhtälö $10x^2 + x - 3 = 0$: \begin{align*} x &= \frac{-1\pm \sqrt{1^2-4\cdot 1 \cdot (-3)}}{2\cdot 10} \\[1mm] &= \frac{-1\pm \sqrt{121}}{20} \\[1mm] &= \frac{-1\pm 11}{20}. \end{align*} Ratkaisuiksi saadaan siis $x_1 = \dfrac{1}{2}$ ja $x_2 = -\dfrac{3}{5}$. Teoreeman 7 nojalla \begin{align*} 10x^2 + x - 3 &= 10\left(x-\frac{1}{2}\right)\left(x+\frac{3}{5}\right) \\[1mm] &= 2\left(x-\frac{1}{2}\right) \cdot 5\left(x+\frac{3}{5}\right) \\[1mm] &= (2x-1)(5x+3). \end{align*}
Jaa seuraavat toisen asteen polynomit ensimmäisen asteen tekijöihin teoreeman 8 avulla. Aloita ratkaisemalla polynomin nollakohdat.
- $x^2+2x-8$
- $9x^2-3x-2$
- $20x^2-2x-6$
- $x^2+2x-8 = (x+4)(x-2)$
- \begin{align*} 9x^2-3x-2 &= 9\left(x - \frac{2}{3}\right)\left(x + \frac{1}{3}\right) \\[2mm] &= (3x-2)(3x+1) \end{align*}
- \begin{align*} 20x^2-2x-6 &= 20\left(x - \frac{3}{5}\right)\left(x + \frac{1}{2}\right) \\[2mm] &= (5x-3)(4x+2) \end{align*}